5 Proven Tips for Mastering Domain and Range Worksheets
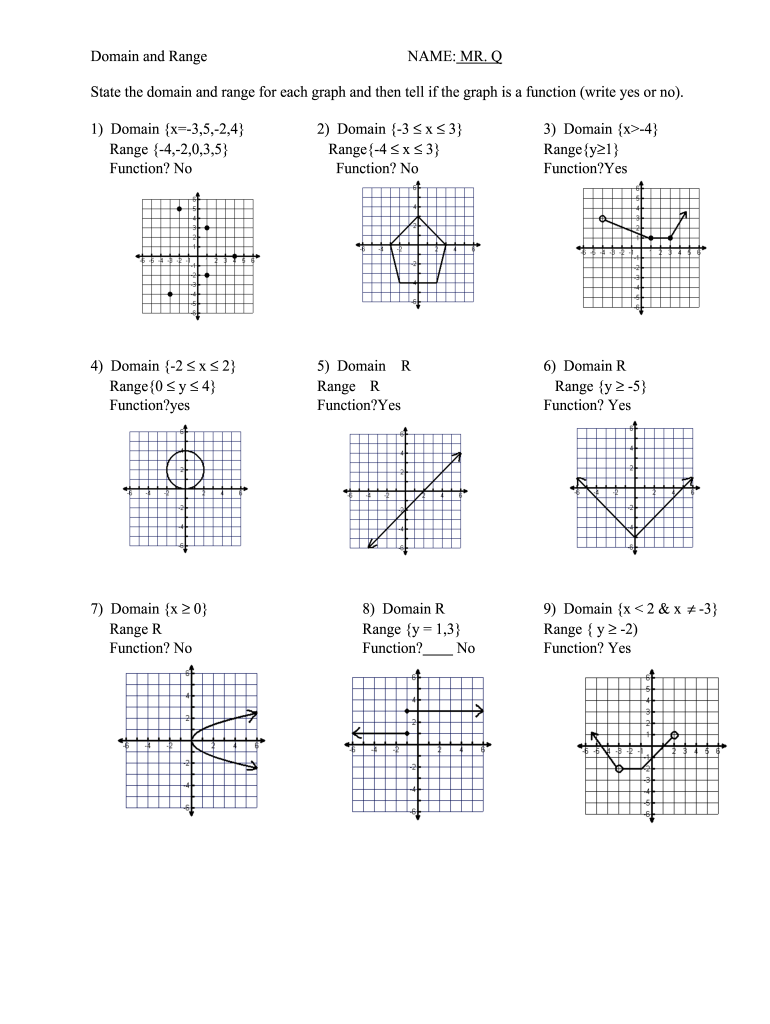
If you've ever sat in a math class and found yourself puzzled by the mysterious realm of domain and range, you're not alone. Many students and professionals struggle to grasp these fundamental concepts. In this post, we're going to delve into how you can master domain and range worksheets through five proven tips. These strategies will enhance your understanding and application of these crucial mathematical concepts, enabling you to confidently tackle any related problem.
1. Understand the Basics

Before diving into the complexity of domain and range, it’s essential to solidify your understanding of these terms:
- Domain: This is the set of all possible input values for which the function is defined. Think of it as what you can “feed” into your function.
- Range: This is the set of all the output values produced by the function from the domain. It’s what the function “spits out”.
Here are some visual aids:
Example:

Consider the function f(x) = x^2. The domain is all real numbers because any number can be squared. However, the range is all non-negative real numbers because a square always results in a positive or zero value.
2. Practice with Real-life Scenarios

One of the best ways to understand domain and range is to apply them to real-life situations. Here’s how you might think of it:
- In Physics: If you’re throwing a ball up into the air, the height of the ball (range) over time (domain) describes a quadratic function, showing how height changes with time.
- In Economics: Cost functions where the price of items (domain) could affect total cost (range) within a defined feasible region.
🔍 Note: Real-life examples help in visualizing how mathematical concepts like domain and range interact with real-world scenarios, making abstract ideas more tangible.
3. Use Visual Tools

Graphical representations are invaluable when dealing with domain and range:
- Create graphs of functions, highlighting vertical and horizontal lines to determine domains and ranges respectively.
- Use color coding or shading to represent restricted domains and ranges.
- Software tools like Desmos or Geogebra can dynamically plot functions, making it easier to experiment with different functions’ behavior.
4. Master Key Functions and their Properties
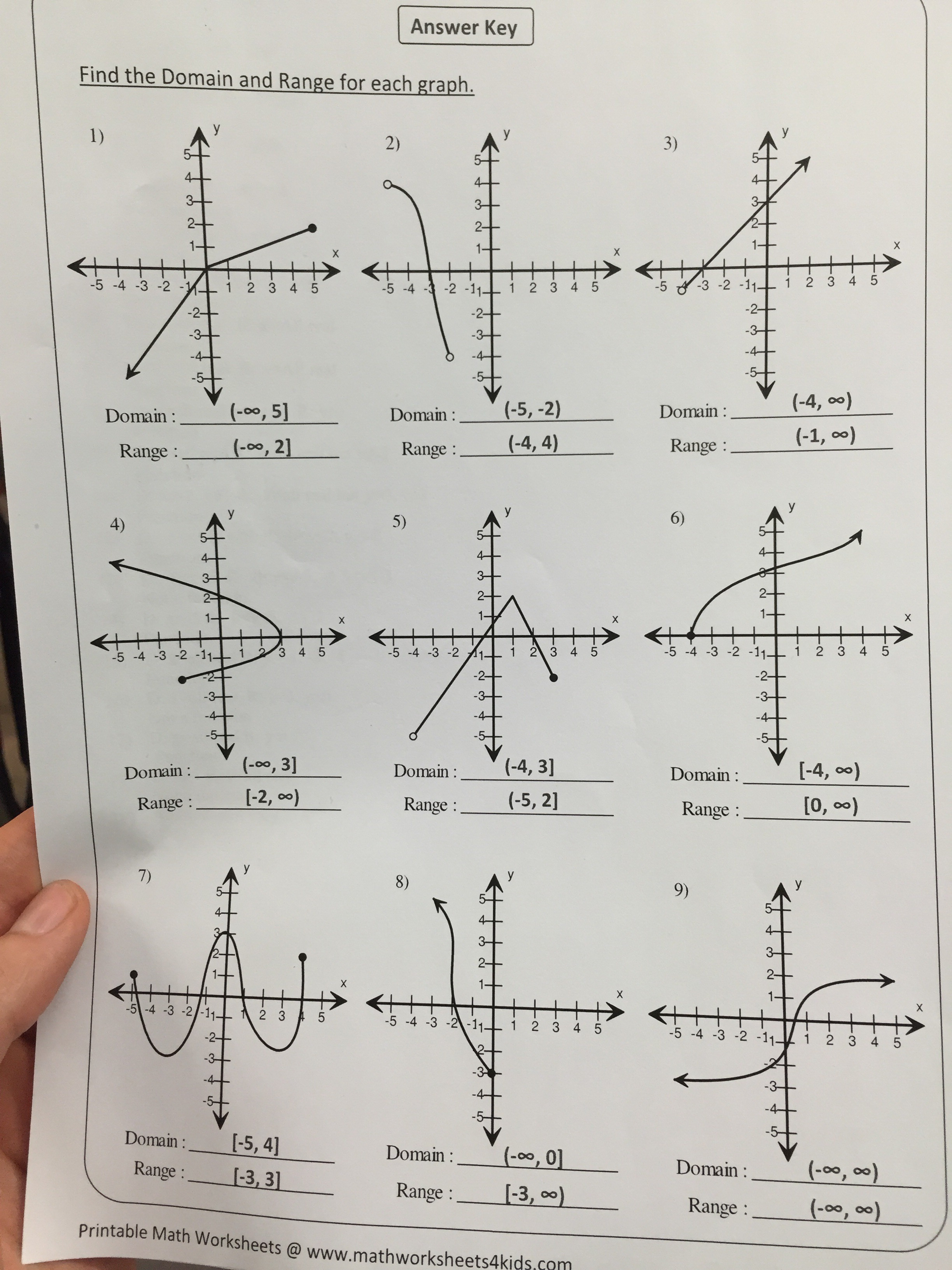
Knowing the standard forms of common functions and their behavior is key:
- Linear functions: Domain is all real numbers, range is also all real numbers.
- Quadratic functions: Domain all real numbers, range might be restricted depending on the direction of the parabola.
- Trigonometric functions: Their domains and ranges are cyclical and need understanding of their periodicity.
- Rational functions: They often have restricted domains where the denominator equals zero.
- Exponential functions: Domain is all real numbers, range depends on whether the base is greater or less than 1.
5. Solve Problems Systematically

Here’s how you can approach worksheet problems methodically:
- Read the problem carefully, understanding what is given and what needs to be found.
- Determine the function. Write it down if necessary.
- Evaluate the function’s domain by identifying any values that would make the function undefined (e.g., division by zero, square roots of negative numbers).
- Check the range by analyzing the function’s output for the domain values, often considering critical points like asymptotes, maximums, and minimums.
- Graph the function or use a graphing tool to visualize the results.
- Summarize your findings in terms of sets or intervals.
📝 Note: Always check for any potential implicit constraints or assumptions in the problem statement.
By internalizing these tips and consistently applying them, you'll find that working with domain and range becomes second nature. These skills not only enhance your ability to solve mathematical problems but also prepare you for more advanced mathematics and real-world applications where understanding the limits and outputs of functions is crucial. Whether you're calculating profit margins, optimizing algorithms, or studying physical phenomena, the foundational knowledge of domain and range will serve you well. The journey to mastering these concepts might seem daunting, but with practice and the right approach, you'll unlock doors to understanding complex mathematical relationships in an intuitive and insightful way.
What are some common mistakes when finding domain and range?

+
One of the most common mistakes is ignoring the square root or division by zero restrictions when determining the domain. Also, overlooking the fact that some functions like exponentials can approach but never reach certain values, thus impacting the range, is another frequent oversight.
Can domain and range be infinite?

+
Yes, for many functions like linear or polynomial functions, the domain and range can be all real numbers, which means they are infinite. However, even infinite ranges might have constraints, like being only positive or negative.
How do discontinuities affect the domain?

+
Discontinuities, particularly vertical asymptotes, create holes or jumps in the graph of a function, which means the function is undefined at these points, thus affecting the domain by excluding those values.



