Domain and Range Worksheet 1 Answer Key Free
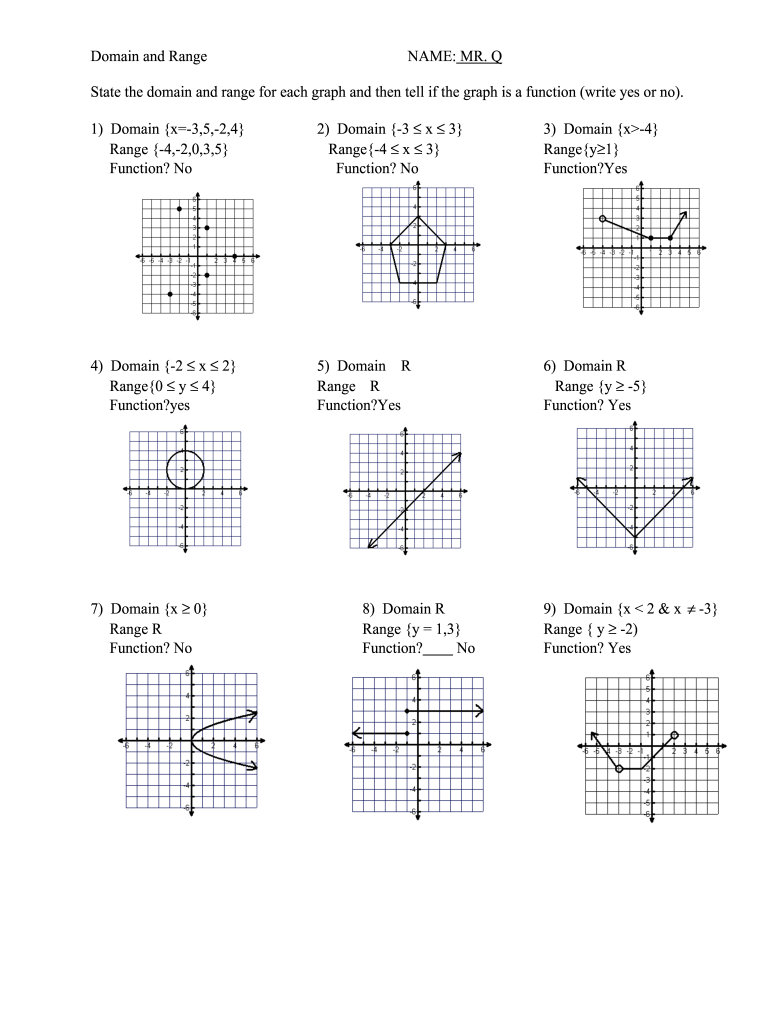
Understanding Domain and Range: A Comprehensive Guide

The domain and range of a function are essential concepts in mathematics, particularly in algebra and calculus. These concepts help us understand the behavior of functions and their limitations. In this article, we will delve into the world of domain and range, providing you with a comprehensive guide to these fundamental concepts.
What is Domain?

The domain of a function is the set of all possible input values for which the function is defined. In other words, it is the set of all values that can be plugged into the function without resulting in an undefined or imaginary output. The domain is often represented by the variable x.
What is Range?

The range of a function is the set of all possible output values that the function can produce. It is the set of all values that can be obtained by plugging in different input values into the function. The range is often represented by the variable y.
Types of Functions and Their Domain and Range

Different types of functions have different domain and range characteristics. Here are some common types of functions and their domain and range:
- Linear Functions: The domain of a linear function is all real numbers, while the range is also all real numbers.
- Quadratic Functions: The domain of a quadratic function is all real numbers, while the range depends on the vertex of the parabola.
- Polynomial Functions: The domain of a polynomial function is all real numbers, while the range depends on the degree of the polynomial.
- Rational Functions: The domain of a rational function is all real numbers except for the values that make the denominator zero, while the range depends on the numerator and denominator.
How to Find Domain and Range

Finding the domain and range of a function can be a straightforward process if you understand the function’s behavior. Here are some steps to help you find the domain and range:
- Domain:
- Identify any restrictions on the input values, such as division by zero or negative numbers under the square root.
- Look for any absolute value or square root functions, which may restrict the domain.
- Consider the type of function, such as linear, quadratic, or polynomial.
- Range:
- Identify any restrictions on the output values, such as the vertex of a parabola or the asymptotes of a rational function.
- Look for any maximum or minimum values that the function can produce.
- Consider the type of function, such as linear, quadratic, or polynomial.
Examples and Solutions
Here are some examples to help you understand how to find the domain and range of different functions:
- Example 1: Find the domain and range of the function f(x) = 1/x.
- Domain: The domain is all real numbers except for x = 0, since division by zero is undefined.
- Range: The range is all real numbers except for y = 0, since the function can never produce a zero output.
- Example 2: Find the domain and range of the function f(x) = x^2 + 2x + 1.
- Domain: The domain is all real numbers, since there are no restrictions on the input values.
- Range: The range is all real numbers greater than or equal to 1, since the function can produce a minimum output value of 1.
Conclusion

In conclusion, understanding the domain and range of a function is crucial in mathematics, particularly in algebra and calculus. By identifying the restrictions on the input and output values, you can determine the domain and range of a function. Practice solving different types of functions, and you will become proficient in finding the domain and range.
What is the difference between domain and range?

+
The domain is the set of all possible input values, while the range is the set of all possible output values.
How do I find the domain of a function?
+
Identify any restrictions on the input values, such as division by zero or negative numbers under the square root. Consider the type of function, such as linear, quadratic, or polynomial.
What is the range of a quadratic function?

+
The range of a quadratic function depends on the vertex of the parabola. If the parabola opens upward, the range is all real numbers greater than or equal to the y-coordinate of the vertex. If the parabola opens downward, the range is all real numbers less than or equal to the y-coordinate of the vertex.
Related Terms:
- Domain and Range Worksheet 2



