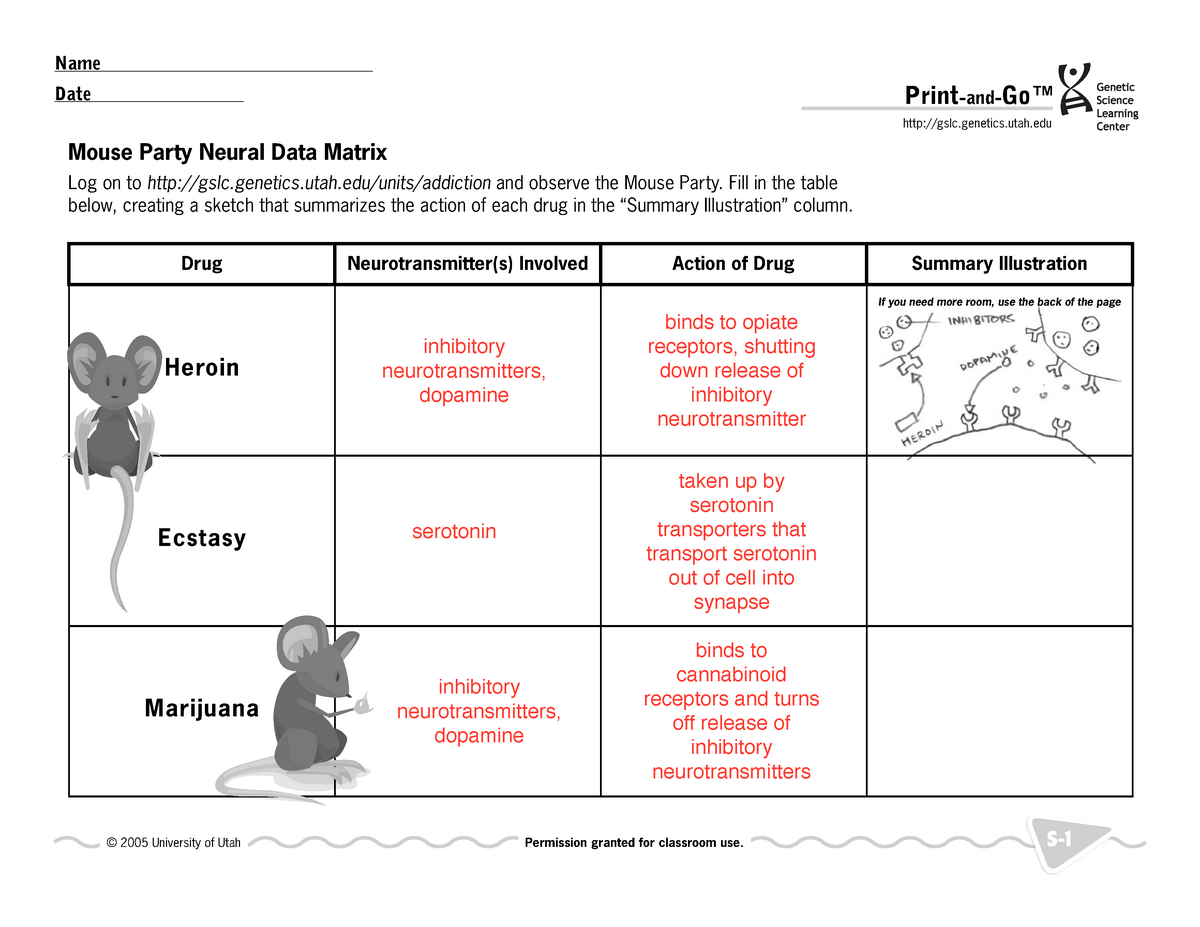
Domain And Range Worksheet #1 Answer

When it comes to understanding functions in mathematics, especially in algebra and precalculus, one of the foundational concepts you'll encounter is the domain and range of a function. This worksheet guide will explore how to determine the domain and range of various functions, focusing on quadratic, linear, exponential, and logarithmic functions, among others.
Understanding Domain
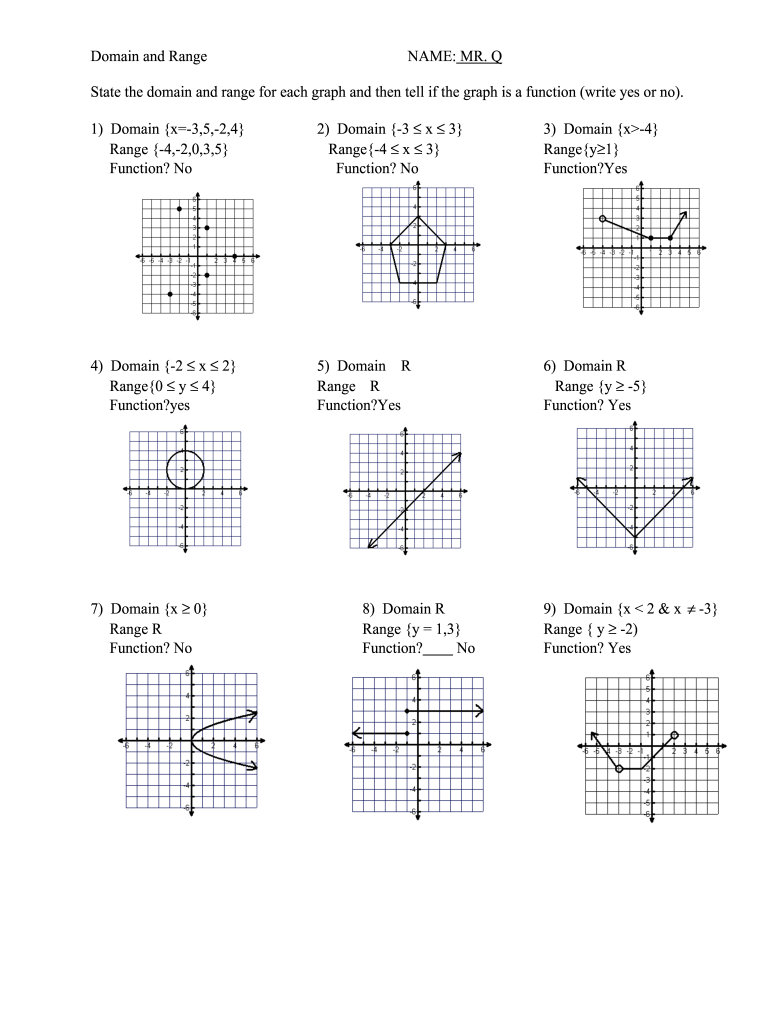
The domain of a function refers to all possible input values (x-values) for which the function is defined. Here are the key rules to determine the domain:
- No Division by Zero: Avoid any value that makes the denominator zero.
- No Square Root of Negative Number: If the function involves square roots, the expression under the root must be non-negative.
- Logarithm Domains: The argument of a logarithmic function must be positive.
Examples of Determining Domain

- For the function (f(x) = \frac{1}{x - 2}):
- The domain excludes (x = 2) because it would result in division by zero.
- Thus, the domain in interval notation is ((-\infty, 2) \cup (2, \infty)).
🔍 Note: In inequality notation, (x \neq 2) represents all real numbers except 2.
- For the function f(x) = \sqrt{x + 1}:
- The domain requires x + 1 \geq 0, so x \geq -1.
- Hence, the domain is [-1, \infty).
Understanding Range
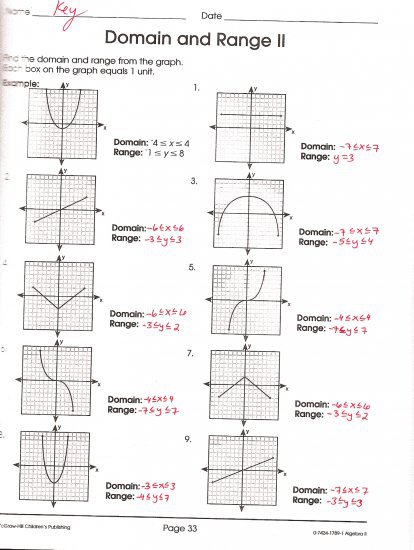
The range of a function refers to all possible output values (y-values) that the function can produce. Here’s how to determine it:
- Linear Functions: The range covers all real numbers unless restricted by a domain.
- Quadratic Functions: The range depends on whether the parabola opens upward or downward.
- Exponential and Logarithmic Functions: These have specific patterns for their ranges.
Examples of Determining Range
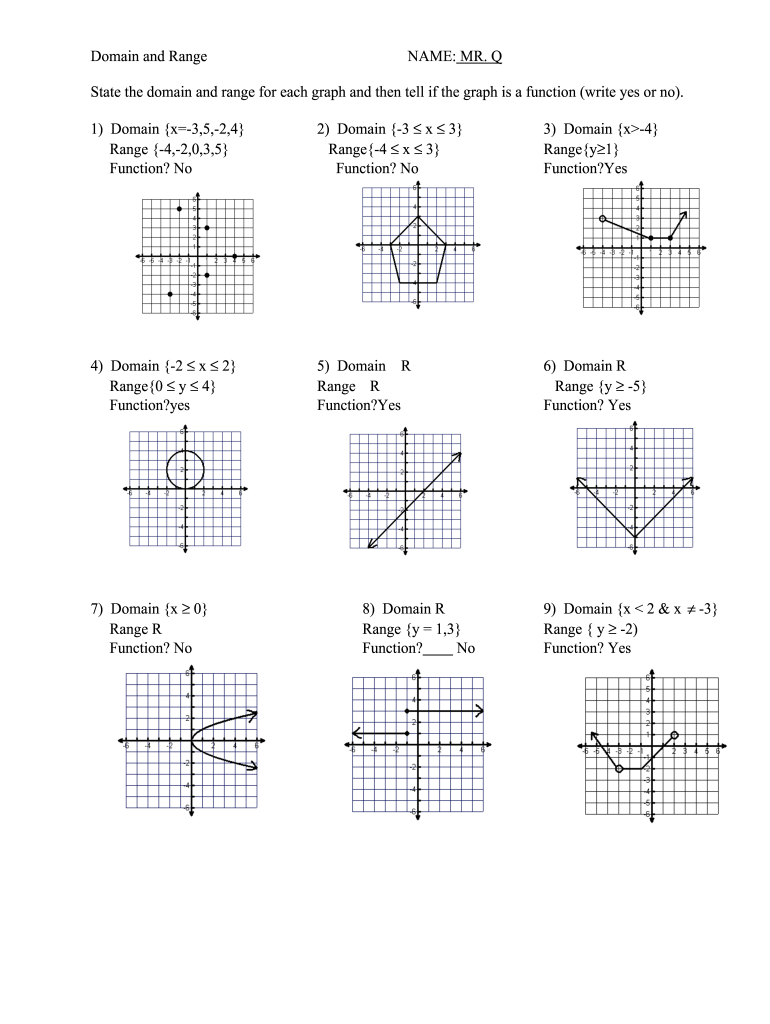
- For (f(x) = x^2 + 3):
- Since (x^2) is always non-negative, the smallest value (f(x)) can be is 3.
- Therefore, the range is ([3, \infty)).
- For f(x) = \frac{1}{x}:
- As x approaches infinity, f(x) approaches 0 from above.
- The range is (-\infty, 0) \cup (0, \infty).
Worksheet Exercises

Here are some exercises for you to practice:
| Function | Domain | Range |
|---|---|---|
| (f(x) = \frac{x}{x + 4}) | (x \neq -4) | ((-\infty, -1) \cup (-1, \infty)) |
| (g(x) = \sqrt[3]{x}) | All real numbers | All real numbers |
| (h(x) = \log_2(x - 5)) | (x > 5) | All real numbers |
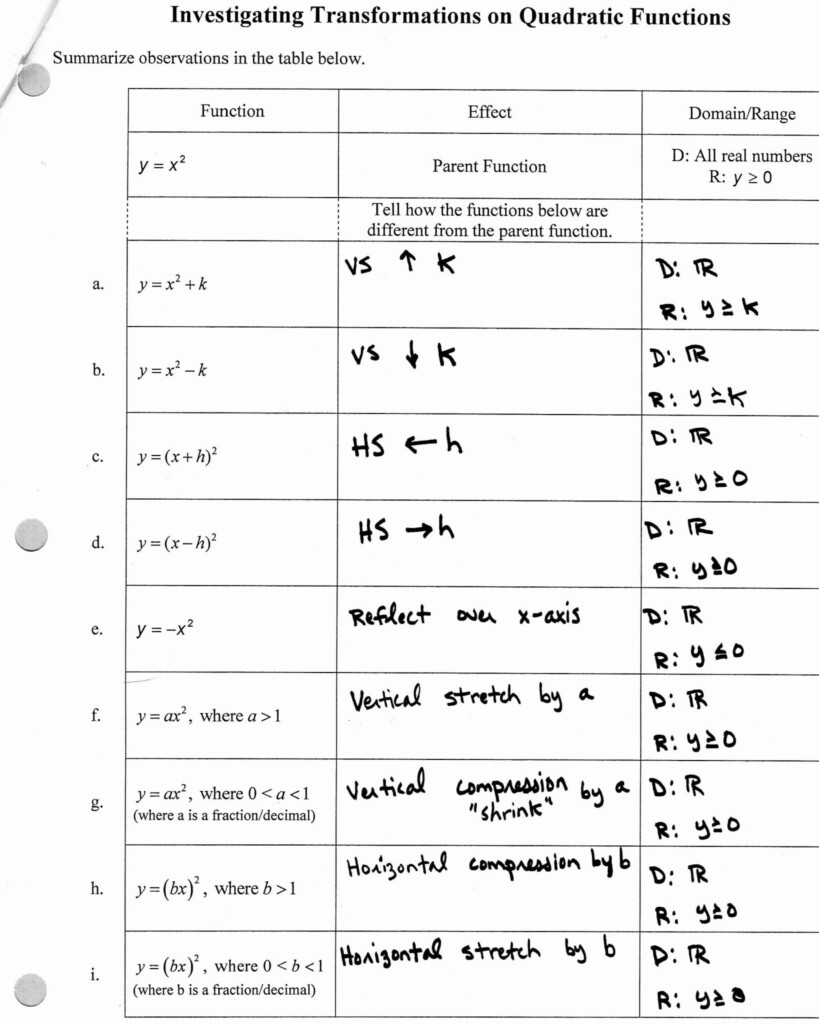
💡 Note: When dealing with functions, always check if the domain and range align with the function's natural behavior or if they are constrained by additional conditions.
To wrap up, understanding domain and range is crucial for graphing functions, solving equations, and interpreting real-world problems. By applying the rules for domain determination and recognizing the inherent properties of various functions, you can accurately describe their behavior. Remember, while some functions have domains that can be directly derived from the function rule, others might require additional mathematical manipulation to fully understand their domain and range. Keep practicing with different functions to master these concepts!
What happens if I can’t find the domain of a function?

+
If you’re struggling with finding the domain of a function, consider each operation in the function individually. Check for restrictions like division by zero, square roots of negative numbers, or logarithms with non-positive arguments. Also, look at the context or any given conditions that might restrict the domain further.
Can the range of a function be different from its domain?

+
Yes, the range and domain of a function can be entirely different sets of numbers. For example, the function (f(x) = x^2) has all real numbers as its domain, but its range is only the non-negative numbers, which is only half of its domain.
How do I know if a function is increasing or decreasing based on domain and range?

+
Domain and range alone do not indicate whether a function is increasing or decreasing. You need to look at the function’s derivative to determine this. A positive derivative suggests an increasing function, while a negative one indicates a decreasing function within certain intervals.