5 Essential Tips for Mastering Function Domains and Ranges

Understanding Function Domains and Ranges: A Comprehensive Guide

The mathematical concepts of function domains and ranges can often seem daunting. However, understanding these concepts is crucial for anyone diving into higher-level mathematics or science. Here are five essential tips to help you master these foundational principles:
1. Define What a Domain and Range Are
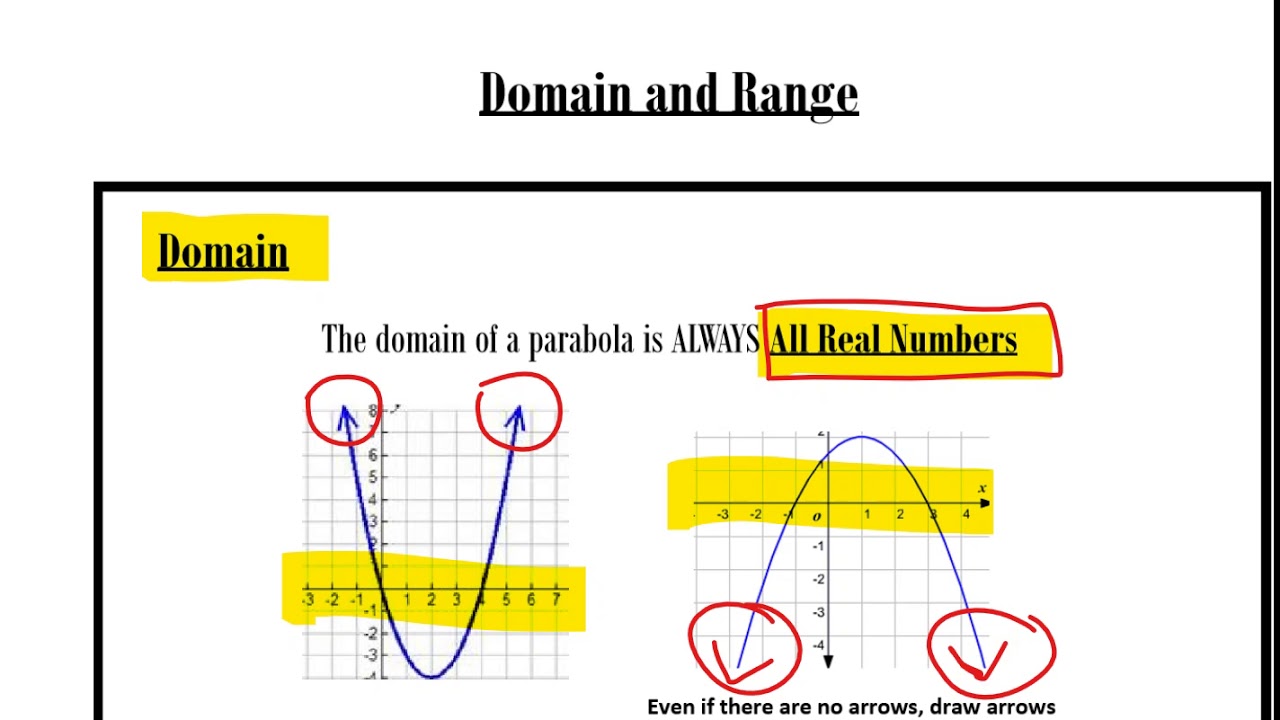
At the heart of functions in mathematics lies the domain, which is the set of all possible input values (x-values) for which the function produces a defined output, and the range, which consists of all possible output values (y-values). Understanding the definitions of these terms is the first step:
- Domain: This is the set of all real numbers for which the function is defined. Essentially, it's what you put into the function.
- Range: This is the set of all real numbers the function outputs when fed the domain values. It's what you get out of the function.
2. Identify Common Exclusions in Domains
Not all numbers can be used as inputs in every function. Here are some common reasons for excluding certain values from the domain:
- Denominator Can't be Zero: For functions with denominators, the domain cannot include any values that would make the denominator zero, as division by zero is undefined.
- Even Roots and Non-Negative Numbers: If a function involves even roots (like square roots or other even roots), the domain must be limited to non-negative numbers to avoid imaginary solutions.
- Logarithmic Functions: The argument inside a logarithm must be positive. Therefore, you'll find that the domain for functions like
log(x)excludes all non-positive numbers.
3. Visualize Functions with Graphing Techniques

Graphing a function can significantly aid in understanding its domain and range:
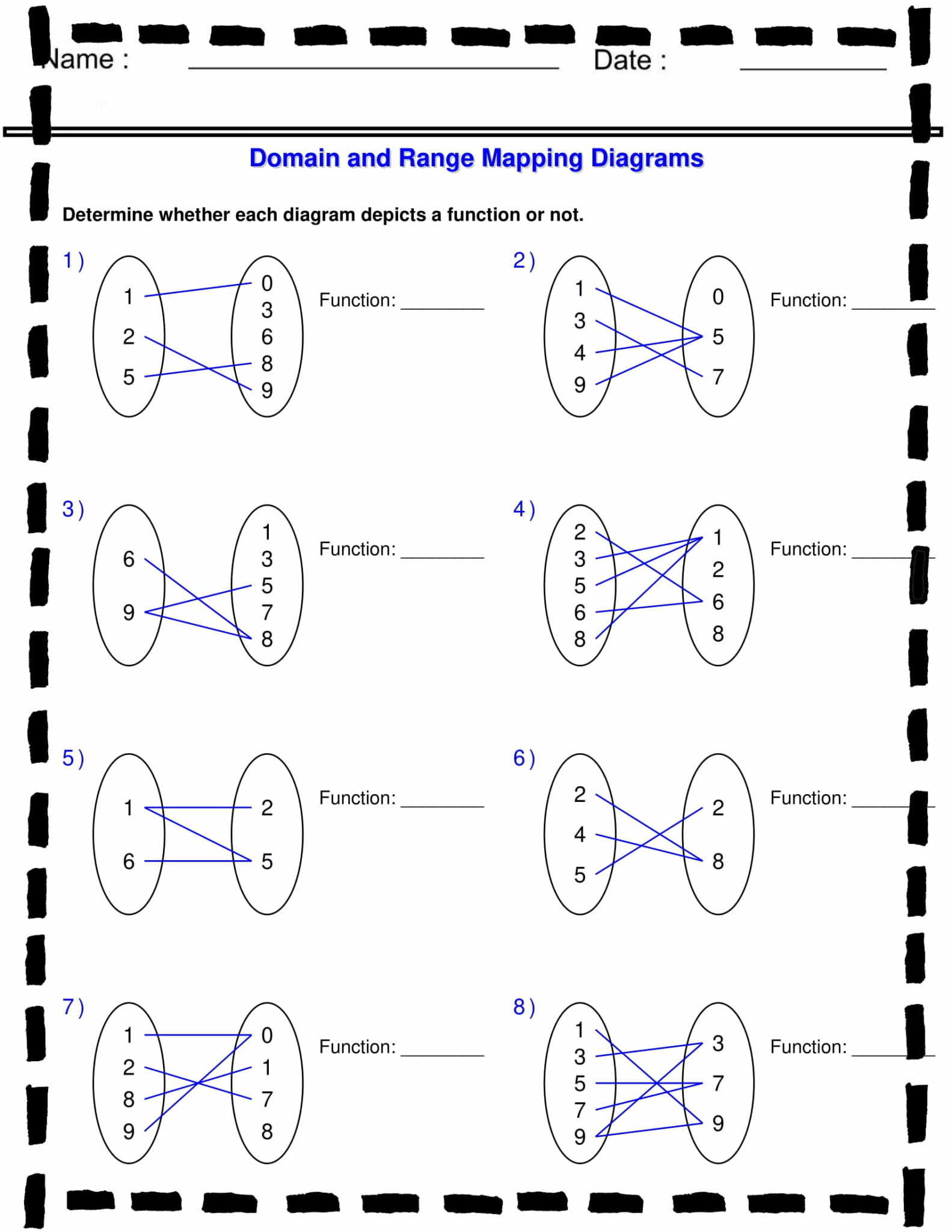
- Horizontal Line Test: Use this test to determine the one-to-one nature of the function. If any horizontal line intersects the graph of the function at most once, the function is one-to-one, meaning the range of the function covers all y-values in its domain of definition.
- Vertical Line Test: This test helps determine if a graph represents a function. If any vertical line intersects the graph more than once, then the relation isn't a function because it fails to pass the test for uniqueness of input to output mapping.
📌 Note: While graphing techniques are useful, they are not foolproof for all functions, particularly those that are piecewise or have discontinuities.
4. Practice Evaluating and Solving Functions

By engaging in exercises where you solve for domain and range, you not only sharpen your mathematical skills but also deepen your understanding:
| Function | Domain | Range |
|---|---|---|
| y = 1/x | all x ≠ 0 | all y ≠ 0 |
| y = √x | x ≥ 0 | y ≥ 0 |
| y = log(x) | x > 0 | all real numbers |
📝 Note: Remember, when finding the range, consider the behavior of the function as x approaches positive or negative infinity, if applicable.
5. Utilize Mathematical Software or Online Calculators

Even the most adept mathematicians can benefit from technological aids:
- Graphing Calculators: Tools like the TI-84 Plus or Desmos allow for immediate visualization and manipulation of functions.
- Symbolic Algebra Programs: Software like Mathematica or Maple can solve complex equations symbolically, providing insight into functions' behaviors.
Mastering function domains and ranges doesn't just involve memorization; it requires a conceptual understanding and practical application. The tips provided here are your stepping stones to a deeper appreciation of mathematical functions, paving the way for tackling more advanced topics with confidence.
By focusing on these fundamental aspects, you equip yourself with the tools to understand not only how functions behave but also how to manipulate and interpret them in real-world applications.
What is the difference between domain and range?

+
The domain is the set of all possible input values for a function, while the range is the set of all possible output values produced by those inputs. In simpler terms, the domain is what you give to the function, and the range is what you get out of it.
Can a function have the same domain and range?

+
Yes, a function can have the same domain and range. For example, consider the function y = x, where both the domain and range are all real numbers.
How do you find the domain of a function?
+
To find the domain of a function, you:
- Look for any restrictions like division by zero or non-negative square roots.
- Check if the function is defined for all real numbers or if certain values are excluded.
- Solve inequalities or equations to find the set of valid inputs for the function.