5 Tips for Mastering Domain and Range Diagrams
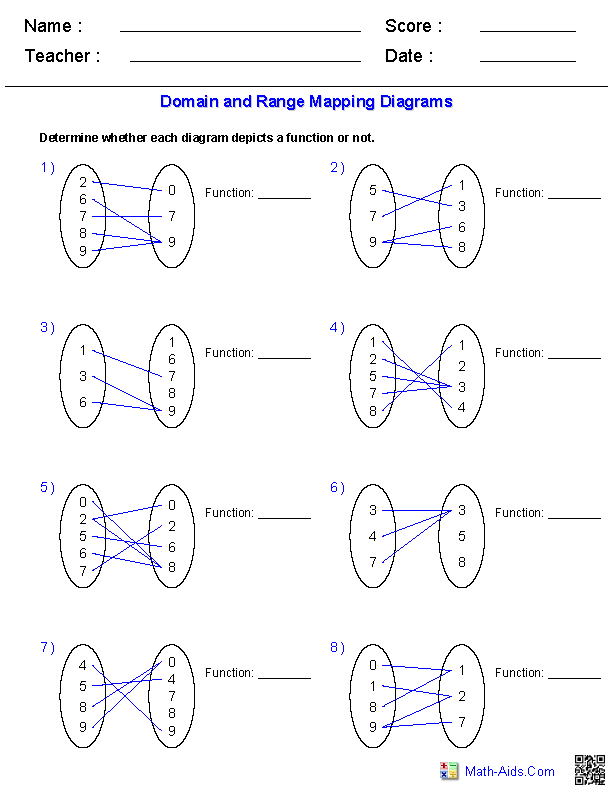
Understanding domain and range diagrams is essential for mastering functions in mathematics. Not only do these diagrams help visualize the inputs and outputs of functions, but they also assist in identifying key characteristics like continuity, intervals of increase or decrease, and symmetry. Here are five expert tips to enhance your grasp on domain and range diagrams:
Tip 1: Understand the Basics of Domain and Range
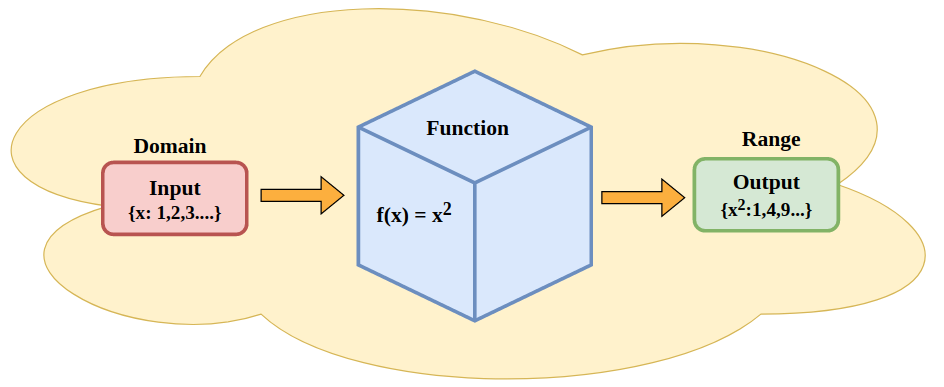
The domain of a function is the complete set of possible values for the independent variable (typically x). The range, on the other hand, consists of all possible values that the dependent variable (usually y) can take. Here's how to master these concepts:
- Define your variables: Before sketching or analyzing a function, determine what your independent and dependent variables represent.
- Identify constraints: Look for any restrictions on x or y, such as dividing by zero, square roots of negative numbers, or logarithm bases less than or equal to 1.
- Visualize the function: Draw or imagine the graph to understand the behavior of the function, which will help in identifying the domain and range.

📝 Note: Some functions, like rational functions, can have holes or vertical asymptotes affecting their domain, whereas trigonometric functions might have vertical asymptotes but no holes.
Tip 2: Use the Vertical Line Test

The vertical line test is a graphical way to determine if a curve represents a function. Here's how to apply it:
- Graph the function: Plot the function or equation on a coordinate plane.
- Draw vertical lines: Imagine or physically draw vertical lines across the graph.
- Count intersections: If any vertical line intersects the graph at more than one point, the relation is not a function.
📝 Note: This test is particularly useful for identifying discontinuities in piecewise functions or complex curves.
Tip 3: Focus on Key Points and Intervals

To thoroughly understand a function's domain and range, focus on:
- Critical Points: Points where the function changes direction or is undefined (like cusps, corners, or asymptotes).
- Intervals: Segments of the domain where the function behaves consistently (increasing, decreasing, or constant).
- Extremal Values: Maximum and minimum values of the function within its range.
These key points and intervals often guide you in sketching or interpreting the domain and range.
Tip 4: Employ Transformations

Transformations of functions can alter their domain and range. Here's how to handle them:
- Horizontal shifts: Shifting a function horizontally doesn't change its range but can affect its domain.
- Vertical shifts: These changes affect the range directly by moving the entire function up or down.
- Vertical Stretching and Compression: Altering the output in the function can stretch or compress the range.
- Reflections: Reflecting a function over the x-axis changes the sign of all range values; reflecting over the y-axis changes the domain.

Tip 5: Practice with Real-World Problems

Applying domain and range diagrams to real-world scenarios enhances understanding:
- Model physical phenomena: Like the speed of a falling object, where the domain represents time and the range represents velocity.
- Business scenarios: Such as profit functions, where the domain might be production volume and the range is profit or loss.
- Biological growth models: Where time as domain correlates with population or size as range.
📝 Note: Real-world applications often include constraints or conditions not visible in pure mathematical models.
In this comprehensive guide to mastering domain and range diagrams, we've explored key tips that should significantly improve your understanding. From grasping the basic definitions to applying practical problem-solving techniques, these tips can transform how you approach mathematical functions and their graphical representations. Remember, continuous practice and application are the keys to mastering these essential mathematical concepts.
What is the difference between domain and range?

+
The domain is the set of all possible input values for the independent variable (usually x). The range is the set of all possible output values or the set of the dependent variable (usually y).
How can I find the domain and range of a function?

+
To find the domain, look for restrictions on x like division by zero or square roots of negative numbers. For the range, analyze the function’s behavior as x changes or look at the graph’s vertical extent.
Can a function have a hole in its domain or range?

+
Yes, functions like rational functions can have holes in their domain due to factors that cancel out in both the numerator and denominator, causing a discontinuity at that point.
What are the effects of transformations on the domain and range of functions?
+
Horizontal shifts affect the domain, vertical shifts affect the range, stretches and compressions modify the range, and reflections over axes change either the domain or the range, depending on the axis of reflection.