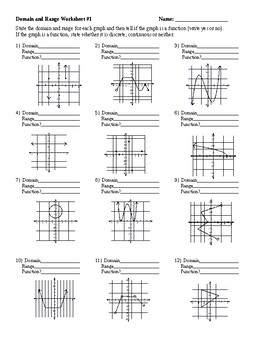
Master Domain and Range: Fun Worksheet Included

In the realm of mathematics, domain and range are fundamental concepts that often perplex students. They’re not just abstract ideas but tools that help in graphing functions and solving equations efficiently. Let’s dive deep into understanding what domain and range mean, how they interact, and why they matter, with a fun worksheet to solidify your knowledge.
What are Domain and Range?

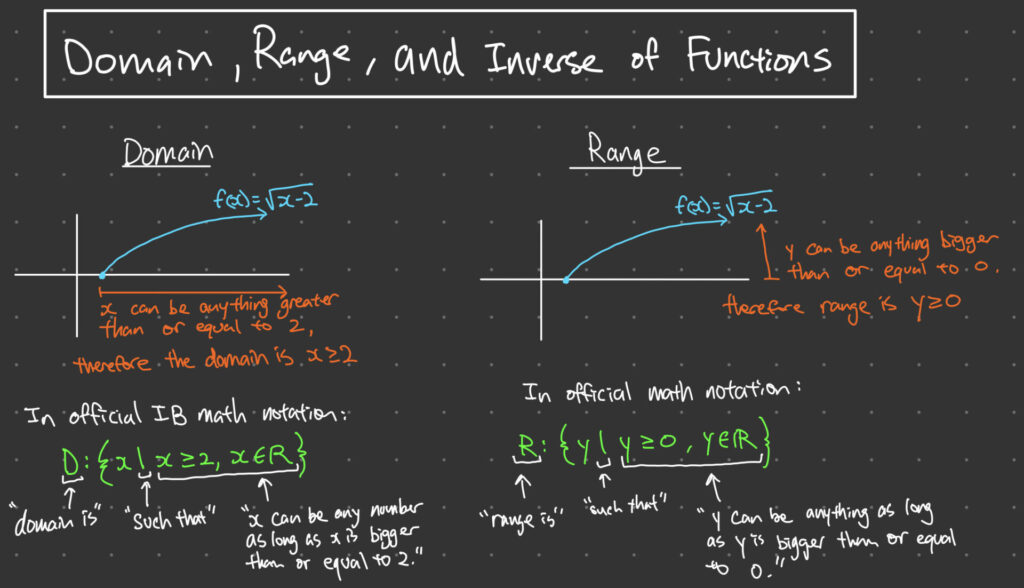
At the heart of every function lies the domain—the set of all possible input values (or x-values) for which the function is defined. The range is then the set of all possible output values (or y-values) that you can obtain from those inputs.
- Domain: This is all the possible inputs you can plug into your function.
- Range: This is all the possible outputs that the function will generate.
Why Do Domain and Range Matter?
Understanding domain and range isn’t just an academic exercise:
- Graphing: Knowing the domain and range helps in sketching the graph of a function accurately.
- Modeling: In real-world applications, understanding limitations on input (domain) and output (range) is essential to create realistic models.
- Solving Equations: Constraints on domain and range can simplify equation solving or can change the number of solutions.
Examples for Clarity

Consider the function f(x) = 1/x:
Domain: Here, x cannot be 0 because division by zero is undefined. Hence, the domain is all real numbers except 0.
Range: The output will never be zero because no real number when divided into 1 will yield zero. Therefore, the range is all real numbers except 0.
How to Find Domain and Range?
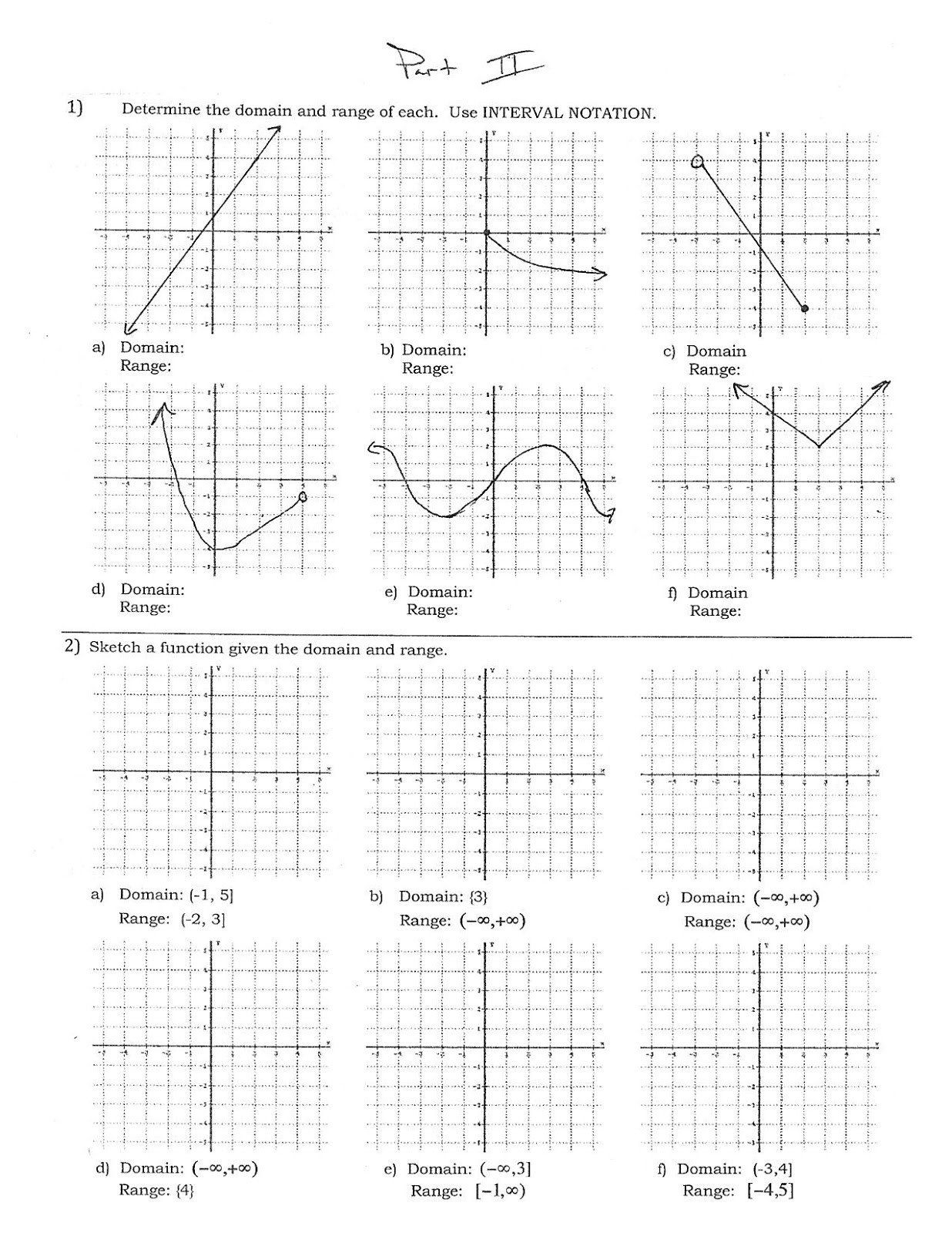
Finding the Domain:
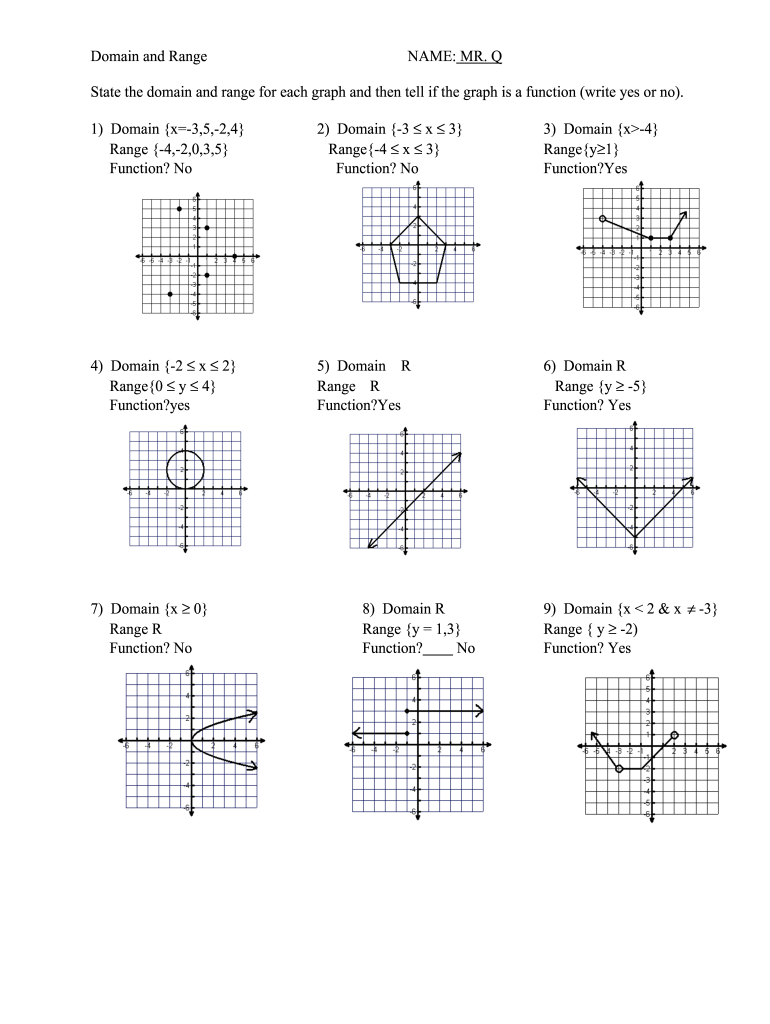
- Read the Function: First, understand what the function does.
- Avoid Undefined Values: Watch out for any operation that would make the function undefined, like division by zero, square roots of negative numbers, or logarithms of negative numbers or zero.
- Restrictions: Sometimes, there are explicit restrictions in the function’s definition or problem statement.
Finding the Range:

- Analyze Output: Consider what outputs are possible for the given function.
- Invert if Possible: In some cases, inverting the function can help visualize or calculate the range.
- Sketch or Analyze: Use graphing or algebraic methods to determine the span of outputs.
Tips for Complicated Functions:

- Graphing: A visual representation often clarifies where the function starts, stops, or has discontinuities.
- Algebra: Solve the function for y and analyze how x influences y.
Interactive Worksheet: Master Domain and Range

Here’s a fun worksheet to solidify your understanding:
| Function | Domain | Range |
|---|---|---|
| y = x² | Real Numbers | [0, ∞) |
| y = √(x) | [0, ∞) | Non-Negative Real Numbers |
| y = 1/x² | Real Numbers Except 0 | (0, ∞) |

📝 Note: Remember that for square roots to be defined, the argument must be non-negative.
Real-World Applications
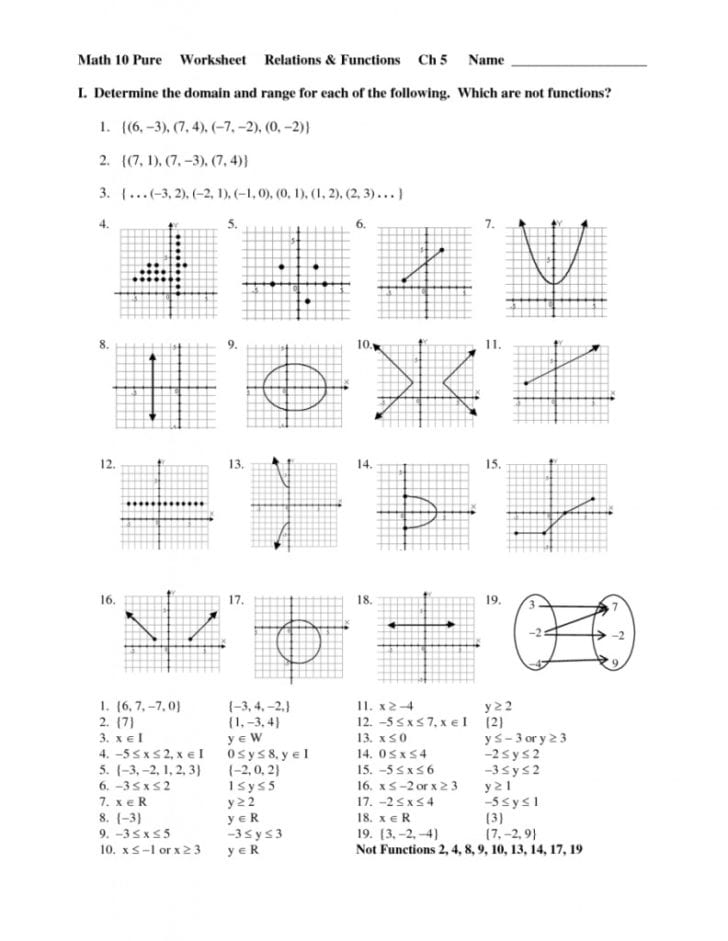
Understanding domain and range extends beyond the classroom:
- Physics: When calculating speed or velocity, constraints on time (domain) and possible speeds (range) are crucial.
- Economics: Models of supply and demand have limits on what prices can be (range) based on what quantities (domain) are supplied or demanded.
- Software Development: Algorithms must account for valid inputs (domain) to produce expected outputs (range).
In Conclusion
Domain and range are not just theoretical constructs; they are practical tools that guide us in modeling, solving, and understanding mathematical problems. By mastering these concepts, you’ll:
- Graph Functions Accurately: Knowing the limits of x and y helps in plotting functions correctly.
- Create More Robust Models: Whether in science, business, or engineering, understanding the bounds of your variables ensures your models make sense in the real world.
- Solve Equations Efficiently: Constraints provided by domain and range simplify equation solving or alter the solution set.
With this comprehensive guide, we’ve explored the essentials of domain and range, provided methods for finding them, and even touched on real-world applications. Use the worksheet as a stepping stone to practice, and remember, understanding these concepts will not only improve your grades but your problem-solving abilities across various fields.
What is the difference between domain and range?
+
The domain refers to all possible input values for a function, whereas the range is the set of all possible output values produced by those inputs.
How does understanding domain and range help in real-world applications?

+
In real-world scenarios, knowing the domain helps define the acceptable inputs for a model or equation, while understanding the range ensures the output is meaningful or feasible in the context of the problem, like in economic models, physics calculations, or software development.
What are some common restrictions on domain?

+
Common restrictions on domain include: - Avoiding division by zero, which excludes certain values from the domain. - Keeping square roots or even roots non-negative. - Logarithms must have positive arguments. - Real-world constraints like time, physical limitations, or economic thresholds.