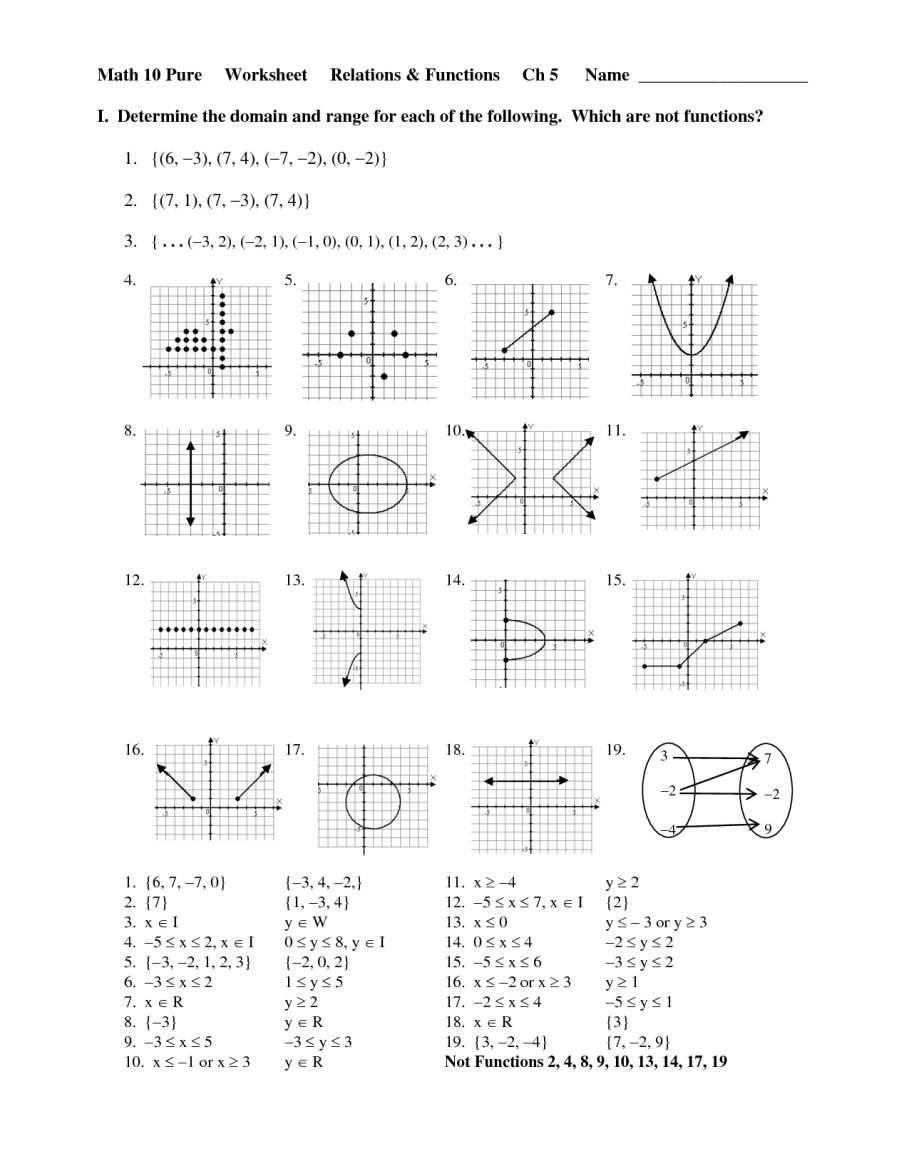
Mastering Domain and Range with Graph Worksheets
Understanding the concepts of domain and range in mathematics can be daunting for many students. However, with the right tools and approaches, these abstract ideas become more tangible. One effective method for mastering these concepts is through graph worksheets, which provide visual aids that help in understanding functions, their domains, and their ranges. This article will explore how you can use graph worksheets to enhance your knowledge of domain and range, provide step-by-step tutorials, and share important tips to simplify learning.
What Are Domain and Range?
Before diving into the practical aspects, let's quickly define what domain and range mean:
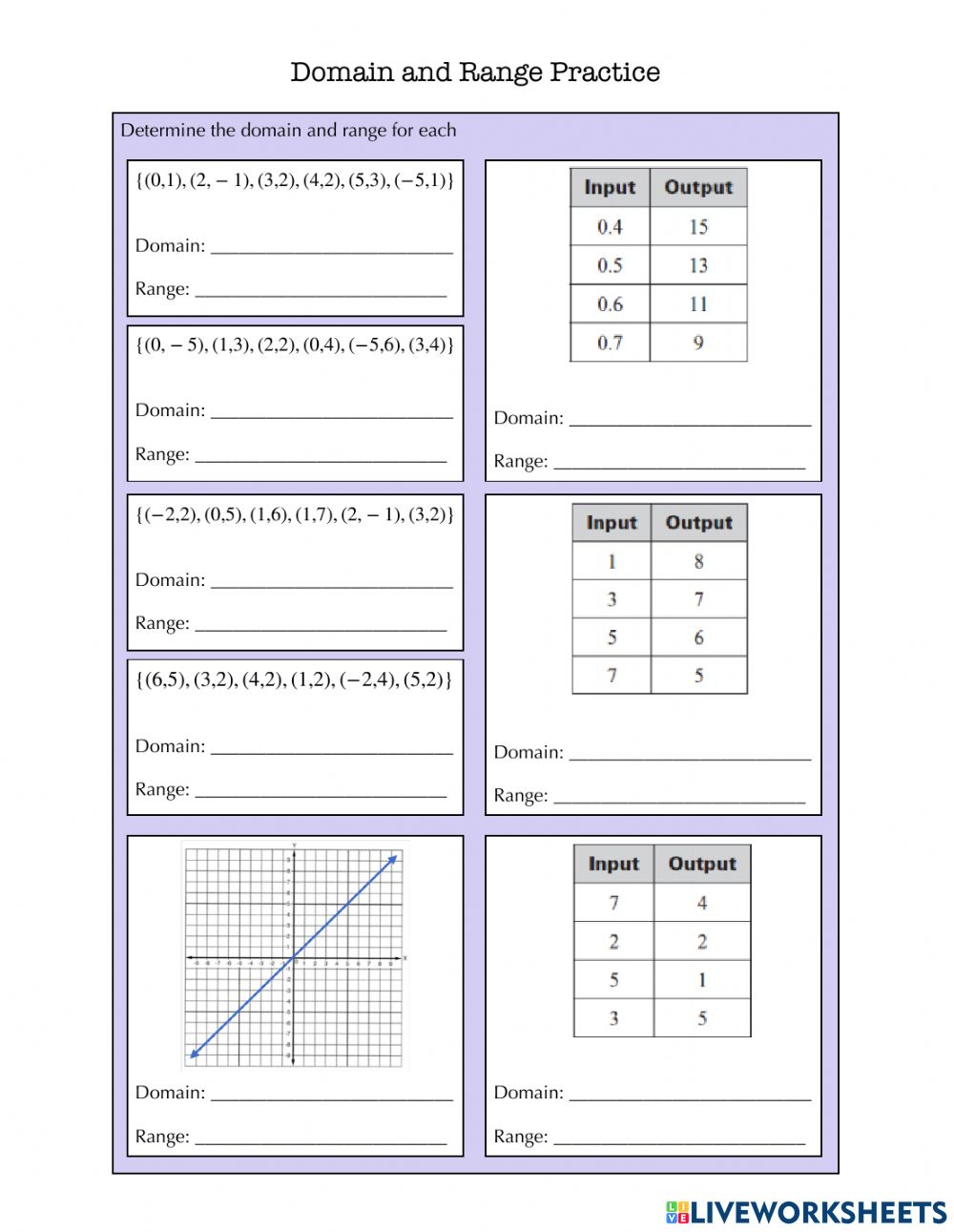
- Domain: The set of all possible input values (x-values) for which the function is defined.
- Range: The set of all possible output values (y-values) that the function can produce.
The Role of Graph Worksheets in Learning Domain and Range
Graph worksheets serve multiple purposes in mathematics education:
- Visual Learning: They offer a graphical representation, making abstract concepts more concrete.
- Practice: Repeated exposure through exercises on these worksheets helps reinforce learning.
- Skill Building: They encourage students to develop critical thinking and problem-solving skills.

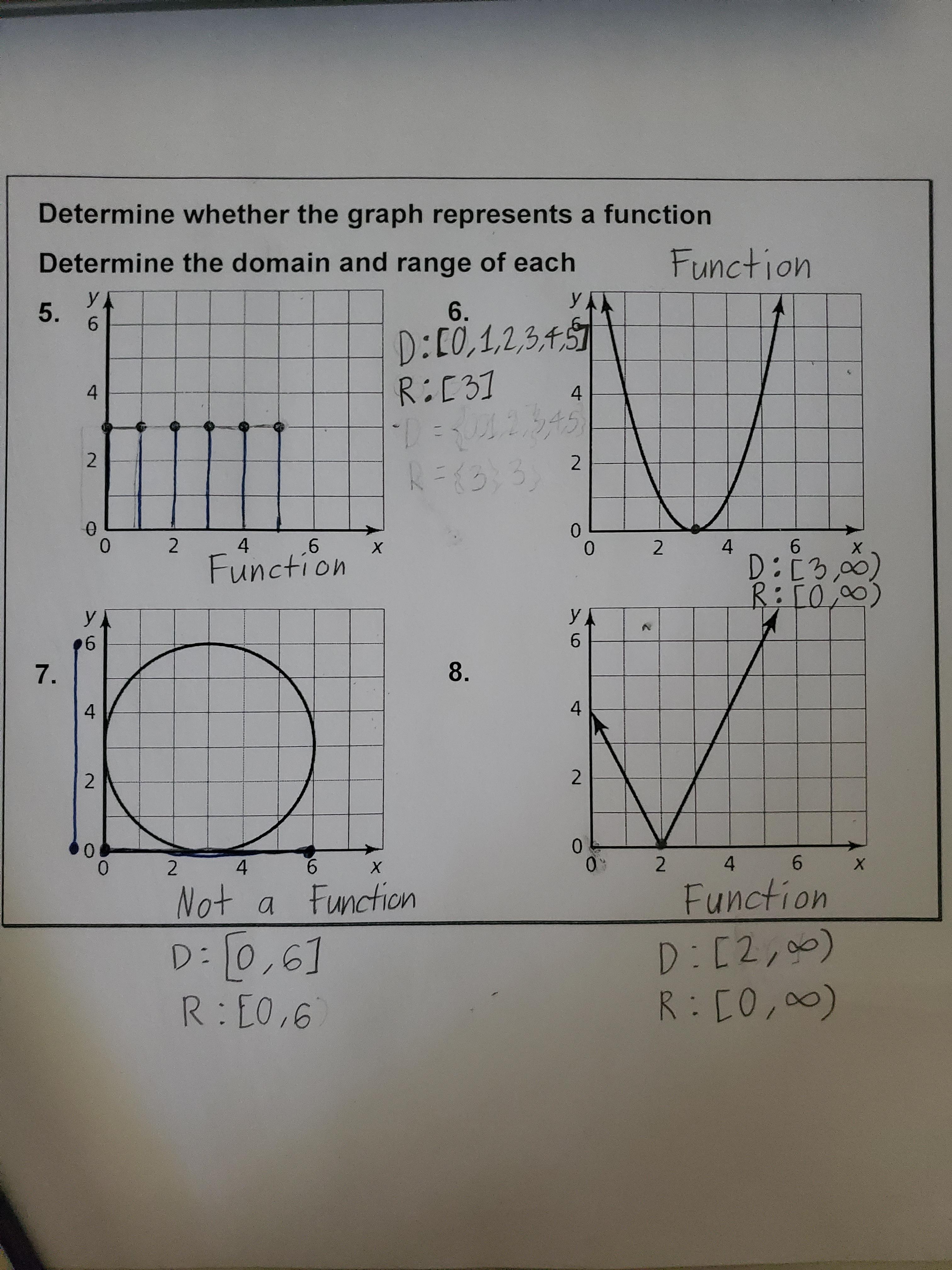
Steps to Master Domain and Range Using Graph Worksheets
Step 1: Understanding the Basics
Start by recalling the definitions:
- Domain is what x can be.
- Range is what f(x) can be.
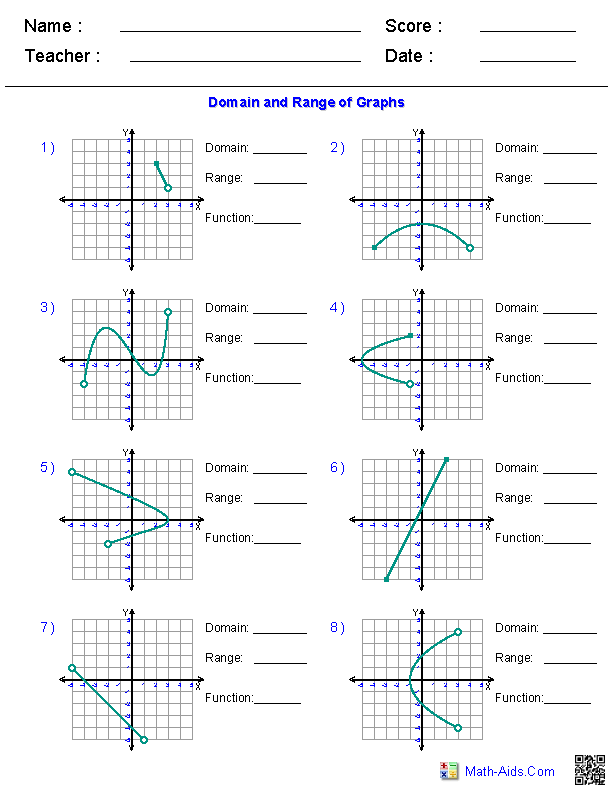
Step 2: Analyzing Graphs
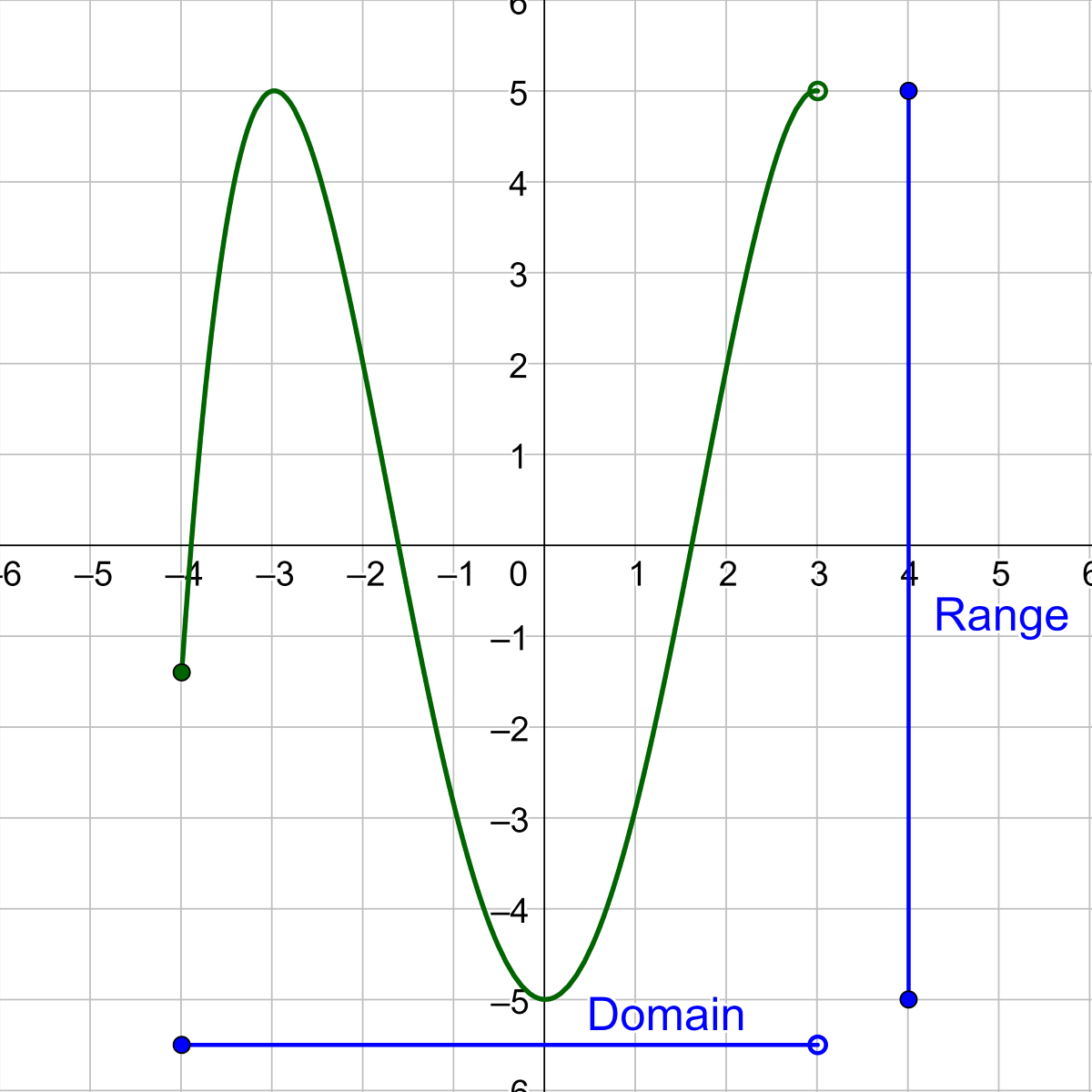
Here’s how to analyze a graph:
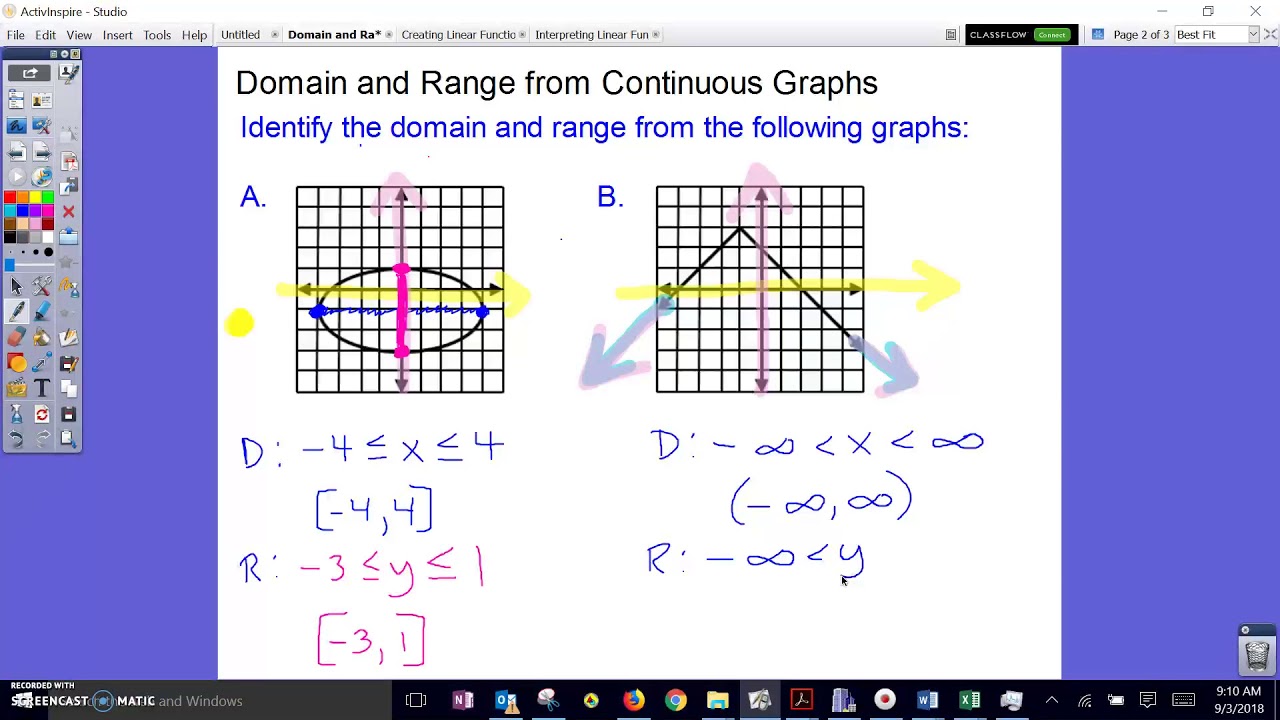
- Identify the x-axis: This represents the domain. Look at where the graph intersects or approaches this axis to determine possible x-values.
- Identify the y-axis: This indicates the range. Notice where the graph extends vertically to understand the output values.
- Check for Discontinuities: Any breaks or holes in the graph indicate values that are not part of the domain or range.
Step 3: Solving Domain and Range
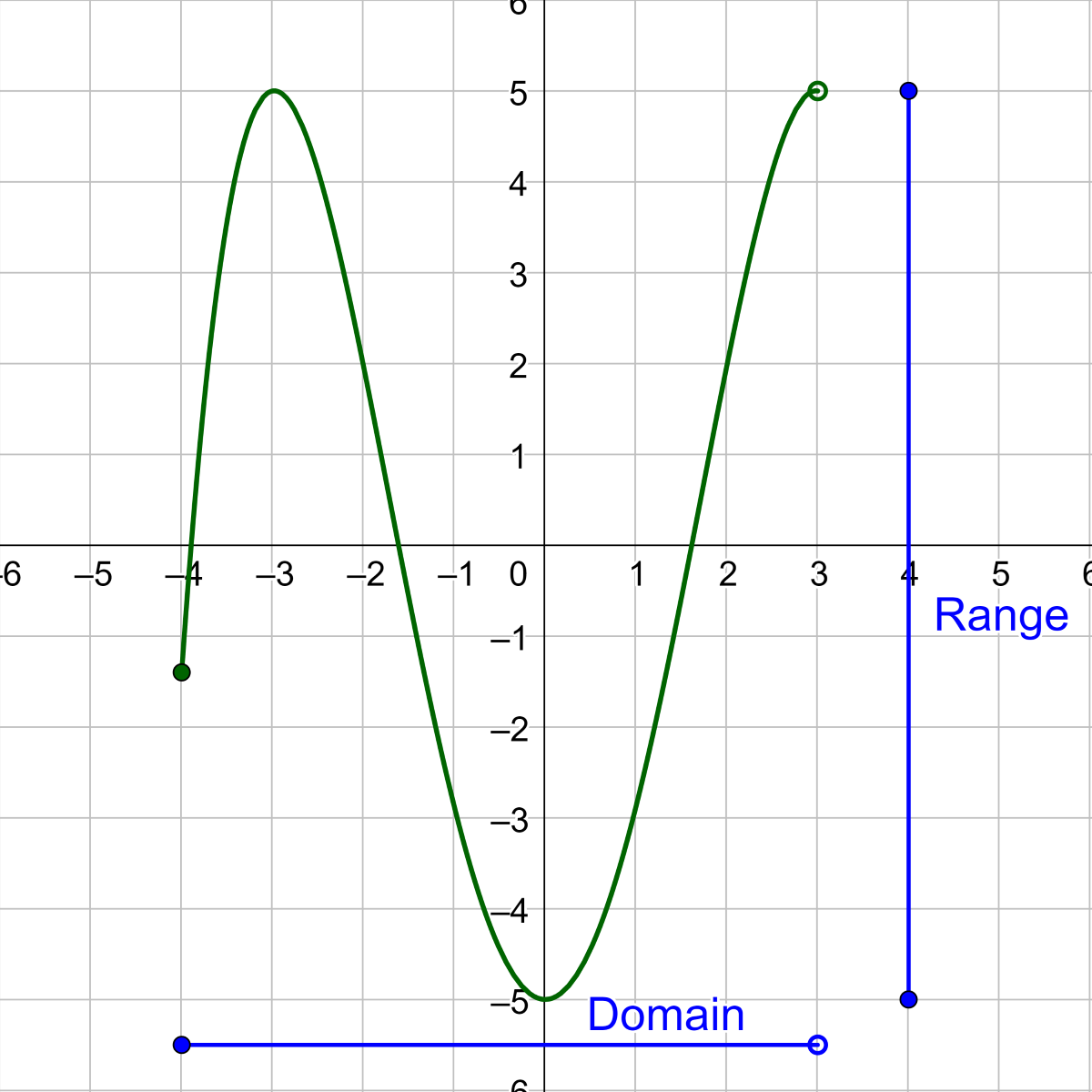
When you work with a graph, follow these steps:
- Examine where the graph begins and ends along the x-axis.
- Identify any vertical asymptotes or restrictions.
- Similarly, look at the vertical extent of the graph for the range.
Step 4: Practice with Examples
Let’s look at a simple example using a graph worksheet:
| Function | Domain | Range |
|---|---|---|
| f(x) = x² | All real numbers (-∞, ∞) | [0, ∞) |
| f(x) = √(x) | [0, ∞) | [0, ∞) |
| f(x) = 1/x | (-∞, 0) ∪ (0, ∞) | (-∞, 0) ∪ (0, ∞) |

⚠️ Note: Remember that the square root function does not accept negative values, affecting its domain.
Conclusion

Mastering domain and range through graph worksheets involves a combination of understanding basic definitions, analyzing graphs effectively, and practicing with various examples. By following the steps outlined above, you’ll find that these initially complex concepts become much clearer. Remember that visualization is a key component in mathematics education, and with repeated practice using graph worksheets, you’ll enhance your analytical skills, making domain and range second nature in your mathematical journey.
What if the graph has a hole or break?
+
A hole or break in the graph indicates that there is a value excluded from the domain or range due to division by zero or restrictions in the function’s definition.
How do asymptotes affect domain and range?
+
Vertical asymptotes define where the function’s domain is limited, and horizontal asymptotes indicate where the function’s range might end or approach infinity.
Can the domain and range be the same?
+
Yes, in functions like f(x) = x, where every x maps directly to y, the domain and range can be the same set of all real numbers.