Divisibility Rules Worksheet: Master Numbers Easily

In a world where numbers are the fundamental elements of mathematics, understanding their properties can not only make math more accessible but can also enhance your problem-solving skills. A divisibility rule is a shorthand method for determining whether a given integer is divisible by another integer without performing the division operation explicitly. Here, we'll embark on a journey through the intricacies of divisibility rules, why they matter, how you can master them, and how to integrate them into worksheets for learning and teaching purposes.
Understanding Divisibility Rules

Divisibility rules act as a set of guidelines that help you quickly determine if one number can divide another evenly. These rules are especially handy in mental arithmetic, mathematical games, or when solving math problems where calculators are not at hand. Here's how they help:
- Speed: They allow for quicker calculations, reducing the time spent on basic arithmetic operations.
- Error reduction: By using well-established rules, you minimize the chance of errors that could occur through long division.
- Practical application: They are useful in real-world scenarios, like when checking if a number of items can be divided evenly among people or groups.
- Mathematical insight: Understanding divisibility helps in grasping more complex mathematical concepts like factors, multiples, and prime factorization.
Divisibility Rules for Key Numbers
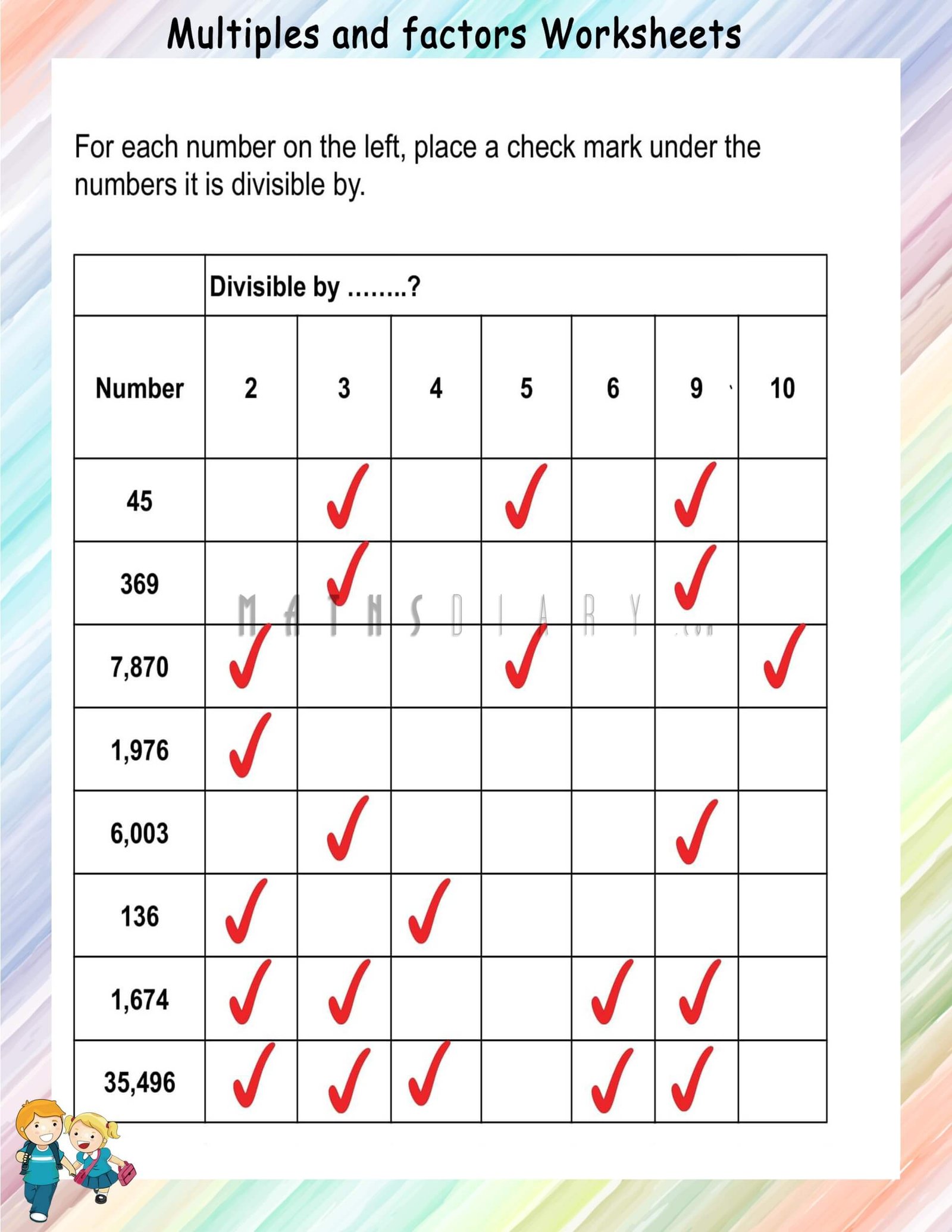
Let's delve into the rules for divisibility by common numbers:
| Divisor | Divisibility Rule |
|---|---|
| 2 | Number ends in 0, 2, 4, 6, or 8. |
| 3 | Sum of digits is divisible by 3. |
| 4 | Last two digits are divisible by 4. |
| 5 | Number ends in 0 or 5. |
| 6 | Divisible by both 2 and 3. |
| 8 | Last three digits are divisible by 8. |
| 9 | Sum of digits is divisible by 9. |
| 10 | Number ends in 0. |
| 11 | Alternating sum of digits is divisible by 11. |

❗ Note: For composite divisors like 6, 8, 9, and 12, divisibility by these numbers often relies on the rules of their prime factors.
Creating a Divisibility Rules Worksheet

To truly master divisibility rules, practicing with a worksheet can be highly effective. Here are some steps to create a comprehensive and engaging worksheet:
- Start with the basics: Include the rules for divisibility by 2, 5, and 10 as an introductory section, since these rules are simpler to understand.
- Build up complexity: Gradually introduce rules for divisibility by 3, 4, 8, 9, and 11.
- Use color coding: Make learning interactive by using different colors for different rules to help visual learning.
- Incorporate exercises: Provide examples where students can apply each rule directly.
- Mixed practice: Include sections where students must determine if a number is divisible by multiple divisors.
- Practical scenarios: Develop scenarios or word problems that reflect real-life situations.
🎓 Note: A worksheet should not just be about memorization but also understanding the underlying principles of divisibility.
Examples and Exercises

Let's explore some exercises that can be included in a worksheet:
- Determine if 210 is divisible by 3, 4, and 11.
- Sum of digits (2+1+0 = 3) is divisible by 3, so divisible by 3.
- Last two digits (10) are not divisible by 4, so not divisible by 4.
- Alternating sum (-1 + 1 + 0 = 0) is divisible by 11, so divisible by 11.
- Find the smallest number greater than 100 that's divisible by 2, 3, and 5.
- Create a number that is divisible by 9 but not by 3.
Utilizing Divisibility Rules in Problem Solving

Once students have mastered divisibility rules through worksheet exercises, they can apply this knowledge in various mathematical contexts:
- Finding LCM and GCD: Least Common Multiple (LCM) and Greatest Common Divisor (GCD) calculations can be made simpler with an understanding of divisibility.
- Prime Factorization: Knowing if numbers share common factors can lead to efficient factorization.
- Fraction Simplification: Easily reduce fractions by identifying and dividing by common factors.
- Modulo Operations: Recognize patterns in remainders when dealing with modulo arithmetic.
- Divisibility Tests for Larger Numbers: Expand the rules to check divisibility by larger composite numbers or powers of primes.
🔢 Note: These skills become increasingly valuable as students move to higher levels of mathematics.
Integrating Divisibility into Other Mathematical Concepts

Divisibility rules open up many doors in mathematics. Here are some areas where they can be further integrated:
- Number Patterns: Identifying patterns in sequences or series often relies on understanding divisibility.
- Algebra: Simplify expressions or solve equations by factoring out common divisors.
- Geometry: Use divisibility to deduce properties of shapes, like the perimeter or area of polygons.
- Cryptography: In modern cryptography, understanding modular arithmetic, which involves divisibility, is crucial for secure communication.
Summing It All Up

Divisibility rules are not merely shortcuts for calculation; they are gateways to deeper mathematical understanding. By mastering these rules, students unlock the ability to perform quick checks, simplify complex problems, and engage with math in a more confident and informed manner. A well-designed worksheet helps in reinforcing these concepts, but the real power lies in the application of these rules to varied mathematical contexts. Whether it's for classroom instruction or self-study, embracing the rules of divisibility can significantly enhance one's mathematical intuition, making numbers not just a series of digits but a world full of patterns and connections.
Why are divisibility rules important for students?

+
Divisibility rules provide a fast and error-resistant way to handle basic arithmetic, foster mathematical insight, and lay a strong foundation for algebra and number theory.
Can a number be divisible by two different rules?

+
Yes, numbers can be divisible by more than one divisor, often following the composite rules like being divisible by 6, which requires divisibility by both 2 and 3.
How can teachers use divisibility worksheets effectively?

+
Teachers should gradually build complexity, encourage mixed practice, use real-life scenarios, and ensure that understanding accompanies memorization.



