5 Easy Tips for Dividing Mixed Numbers and Fractions

Working with numbers can sometimes feel like a daunting task, especially when it comes to dividing mixed numbers and fractions. Whether you're tackling homework, preparing for a test, or simply refreshing your math skills, understanding how to handle these operations can simplify what might seem complex. Here are five easy tips for dividing mixed numbers and fractions, which will empower you to approach math with confidence and ease.
Understand the Basics of Fractions and Mixed Numbers

Before diving into division, it’s crucial to understand the foundational elements of fractions and mixed numbers:
- Fractions consist of a numerator (the number above the line) and a denominator (the number below the line).
- Mixed Numbers combine whole numbers with fractions, e.g., 2 3⁄4.
These concepts will serve as the building blocks for more complex operations like division.

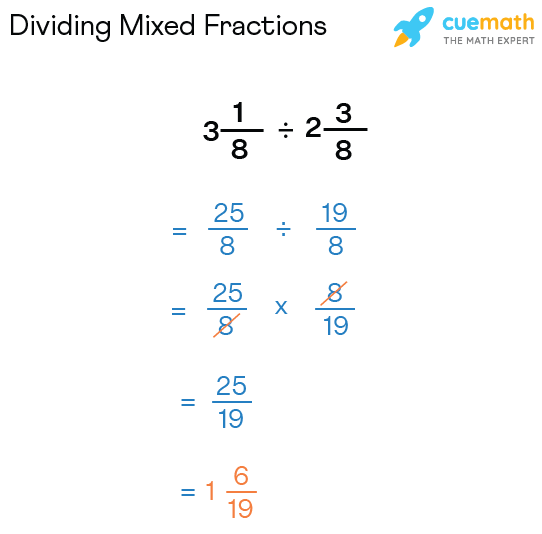
Convert Mixed Numbers to Improper Fractions

To divide mixed numbers, you must first convert them into improper fractions. Here’s how:
- Multiply the whole number by the denominator of the fraction.
- Add the result to the numerator.
- Place this sum over the original denominator.
For example, to convert 2 3⁄4 into an improper fraction:
- (2 * 4) + 3 = 8 + 3 = 11
- Place 11 over the original denominator (4) to get 11⁄4.
Now you can divide as if both numbers were improper fractions.
Use the Reciprocal for Division
Dividing fractions involves an often counterintuitive step: multiplying by the reciprocal:
- Identify the divisor (the number you’re dividing by).
- Take the reciprocal of the divisor. This means flipping the numerator and denominator.
- Multiply the dividend (the number being divided) by this reciprocal.
Here’s a simple example:
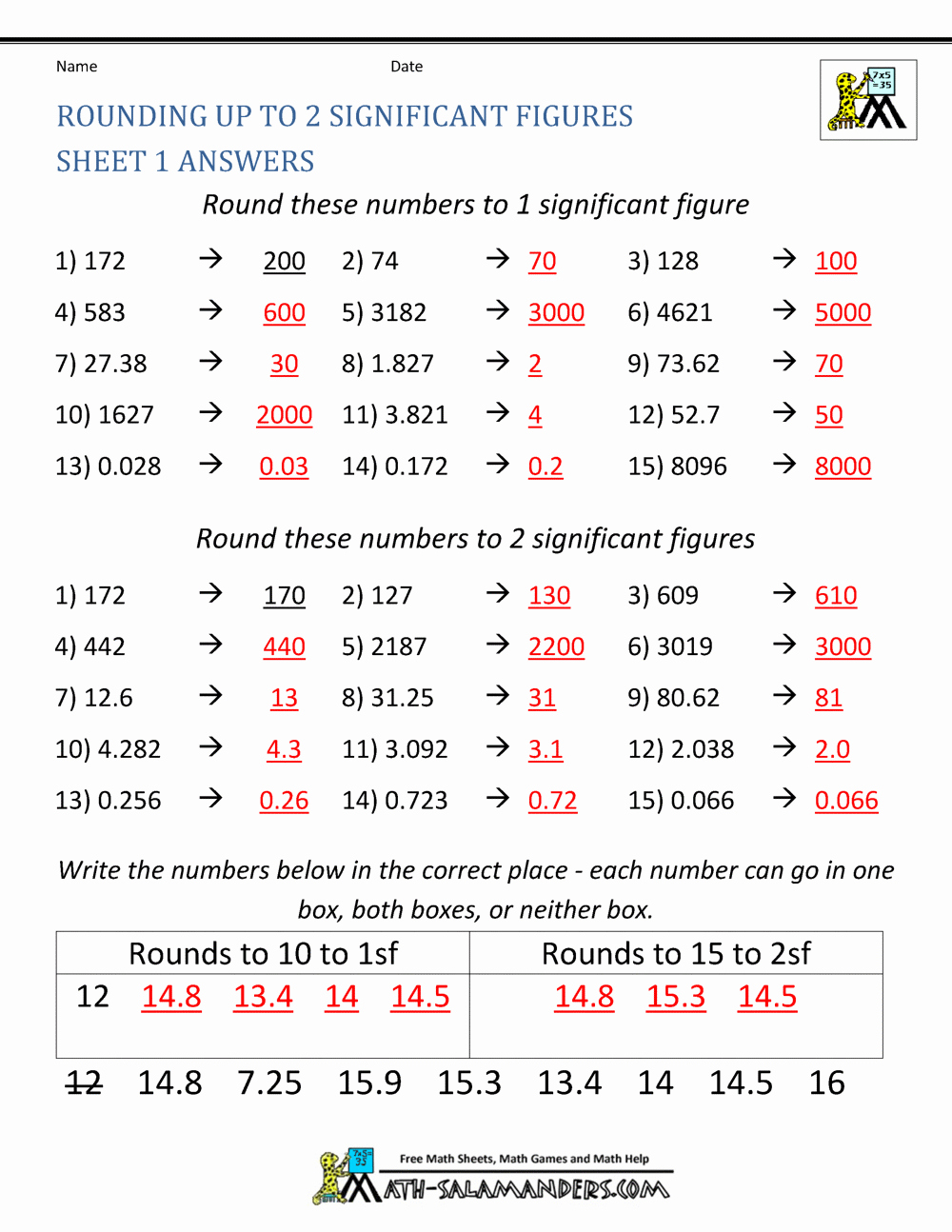
| Original Problem | Convert to Improper | Reciprocal | Multiply | Simplify if possible |
| 2 1⁄2 ÷ 1⁄4 | 5⁄2 ÷ 1⁄4 | 5⁄2 × 4⁄1 | 20⁄2 | 10 |

✅ Note: When multiplying, remember that the product of the numerators over the product of the denominators yields your result.
Reduce Fractions Whenever Possible
Simplification is your ally when working with fractions:
- After multiplication, look for the greatest common divisor (GCD) between the numerator and denominator.
- Divide both by this GCD to get your answer in its simplest form.
If you end up with a numerator larger than the denominator, you might need to convert it back to a mixed number for clarity.

Practice with Different Problems
There’s no better way to solidify these concepts than by engaging with various problems:
- Try division problems with mixed numbers, simple fractions, and combinations of both.
- Create scenarios where you might need to divide in everyday life: dividing pizza slices, measuring ingredients, etc.
- Use online resources or math apps that provide instant feedback for practice.
Each problem you solve strengthens your intuition and proficiency with these techniques.
Mastering the art of dividing mixed numbers and fractions isn't just about doing math correctly; it's about understanding the logic behind these operations. This knowledge not only makes everyday calculations easier but also paves the way for understanding more advanced mathematical concepts. So, keep practicing, keep simplifying, and you'll find that dealing with these numbers becomes intuitive and straightforward.
What’s the easiest way to convert a mixed number into an improper fraction?

+
The easiest way involves three steps: multiply the whole number by the fraction’s denominator, add this to the numerator, and then place this sum over the original denominator.
Why do we multiply by the reciprocal when dividing fractions?

+
Multiplying by the reciprocal changes division into multiplication, which is easier to compute and follow algebraically.
What if I get a fraction as my final answer after division?

+
If your final answer is a fraction, you can either leave it as is or convert it back to a mixed number, depending on the context of your problem or the form you need.
How can I simplify fractions quickly?

+
Look for the greatest common divisor (GCD) between the numerator and the denominator. Then divide both by this GCD to simplify.
Are there common mistakes to avoid when dividing mixed numbers?

+
Yes, avoid not converting mixed numbers to improper fractions first, forgetting to multiply by the reciprocal, and neglecting to simplify your final answer.