Dividing by Fractions: Easy Practice Worksheets

In the world of mathematics, dividing by fractions can seem daunting at first, but with the right approach and practice, it becomes a straightforward task. This blog post is designed to guide students, teachers, and math enthusiasts through the process of dividing by fractions, providing easy-to-understand instructions, examples, and practice worksheets. Whether you're just starting to learn about fractions or need a refresher, let's dive into the nuts and bolts of this essential math skill.
Understanding Division by Fractions

Before we jump into dividing by fractions, it’s crucial to understand what division really means in the context of fractions. Essentially, division by a fraction is the same as multiplying by its reciprocal. Here’s how you can conceptualize this:
- Inverse Operation: Dividing by a number is the inverse of multiplying by that number. Therefore, dividing by a fraction is akin to multiplying by the flip or reciprocal of that fraction.
- Reciprocal: The reciprocal of a fraction is found by swapping its numerator and denominator. For instance, the reciprocal of 3/4 is 4/3.
⚠️ Note: When you are dealing with division of fractions, you always look for the reciprocal because this turns the division into multiplication, which is much simpler to perform.
Example:

Let’s consider dividing 6 by 1⁄2. Instead of dividing, we:
- Flip 1⁄2 to get 2⁄1, which is its reciprocal.
- Multiply 6 by 2⁄1, resulting in 12⁄1 or simply 12.
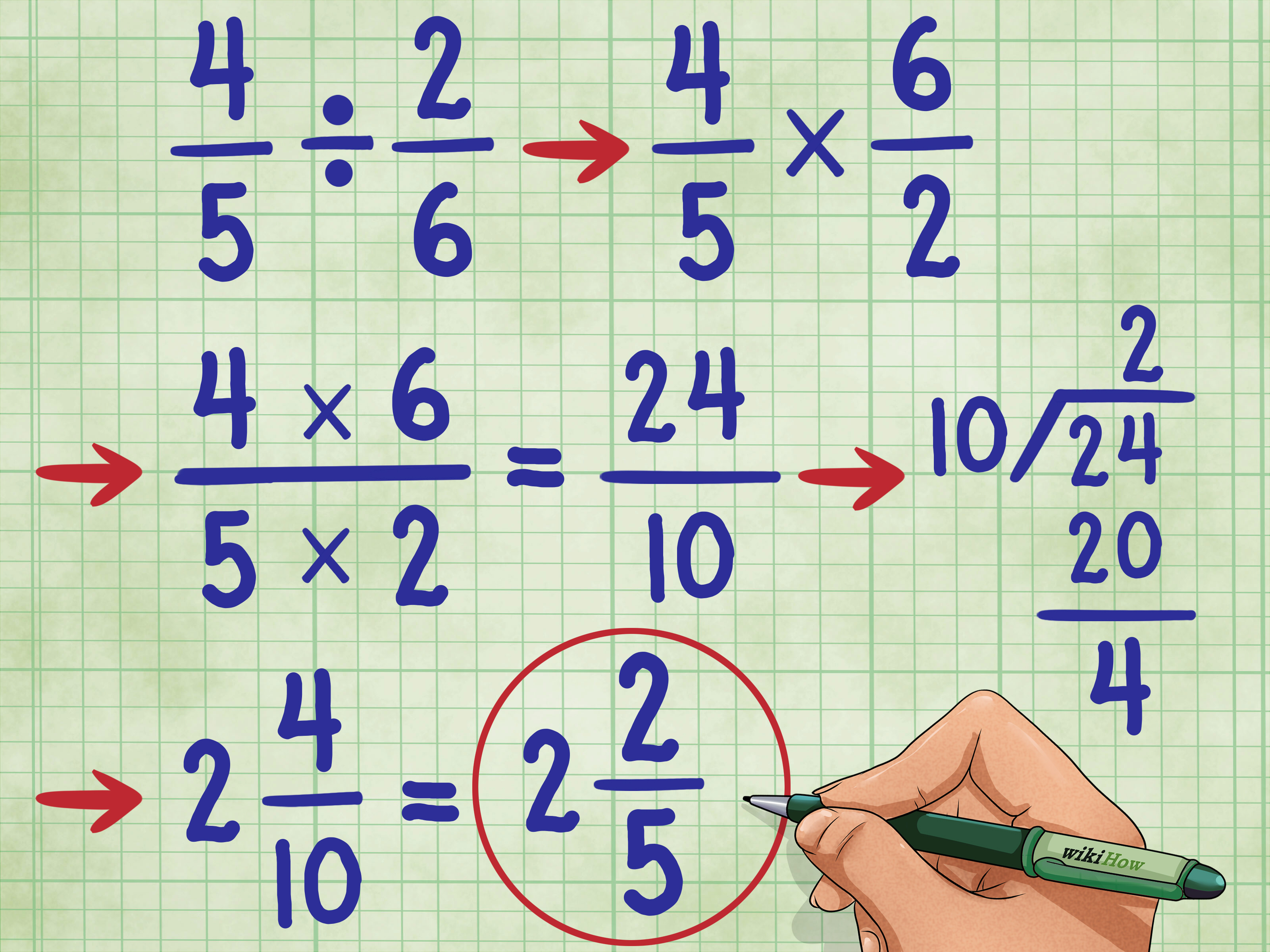
Steps to Divide by a Fraction

Here are the steps to successfully divide by any fraction:
- Find the Reciprocal: Swap the numerator and denominator of the fraction you’re dividing by.
- Multiply: Instead of dividing, multiply the dividend (the number you’re starting with) by the reciprocal of the divisor (the fraction you’re dividing by).
- Simplify if Possible: After multiplication, reduce the result to its simplest form if needed.
Practice Examples:

| Problem | Steps | Solution |
|---|---|---|
| 7 ÷ 1⁄3 |
|
21 |
| 4⁄5 ÷ 3⁄4 |
|
1 1⁄15 |
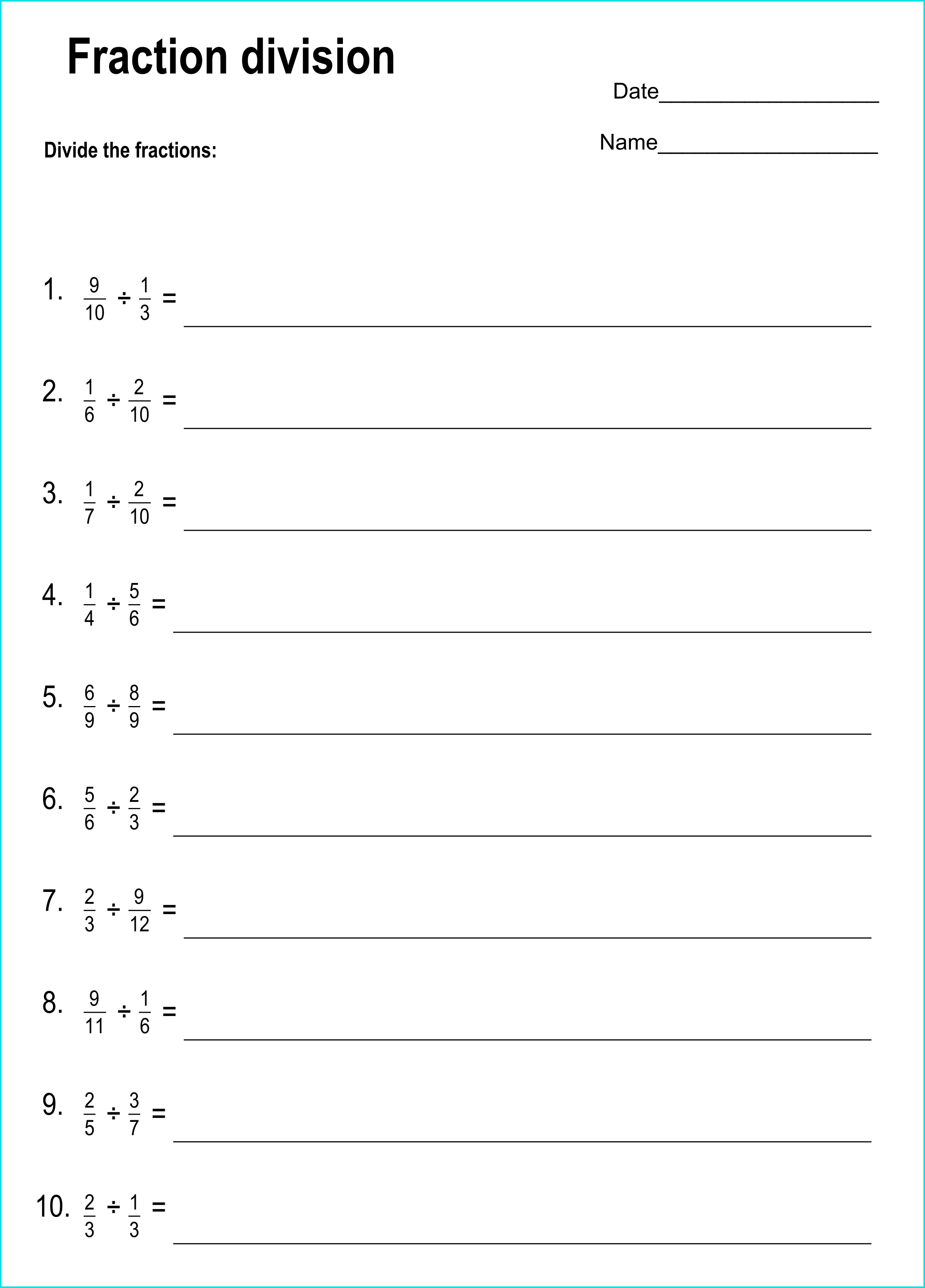
🔎 Note: When dividing mixed numbers, remember to convert them into improper fractions first before proceeding with the division process.
Why Practice is Important

Practice sheets are essential because:
- They help solidify understanding through repetition.
- They provide instant feedback on where mistakes might be occurring.
- They allow for pattern recognition which simplifies future problem solving.
Downloadable Worksheets

To facilitate practice, here are some downloadable worksheets designed for different skill levels:
- Beginner: Simple division of whole numbers by fractions.
- Intermediate: Includes mixed numbers and more complex fractions.
- Advanced: Word problems involving real-life situations where dividing by fractions is needed.
🖨️ Note: Ensure you have a PDF reader installed before downloading.
In conclusion, dividing by fractions is an essential skill that, with the right techniques and ample practice, can be mastered by anyone. Remember to always find the reciprocal, multiply, and simplify if necessary. This approach not only makes the process intuitive but also builds a strong foundation for further algebraic studies.
What is the reciprocal of a fraction?

+
The reciprocal of a fraction is obtained by interchanging the numerator and the denominator. For example, the reciprocal of 2⁄3 is 3⁄2.
Why do we multiply by the reciprocal when dividing fractions?

+
Multiplying by the reciprocal simplifies the operation from division to multiplication, which is generally easier to perform. It’s based on the principle that dividing by a number is the same as multiplying by its inverse.
Can you divide by zero in fractions?
+
No, it is mathematically undefined to divide by zero. If you encounter a fraction where the denominator is zero, it means the expression is undefined, and there is no solution.