Master Division of Polynomials: Free Worksheet Inside

In the vast landscape of algebra, one of the most essential skills to master is the division of polynomials. This process, while seemingly straightforward, can often trip up even the most diligent students due to its procedural complexity. This post will not only guide you through the steps necessary to divide polynomials effectively but also provide you with a free downloadable worksheet to practice your skills. Whether you are a student preparing for an exam or a teacher looking for resources to enrich your curriculum, this guide will demystify polynomial division for you.
The Basics of Polynomials

Before diving into the division of polynomials, it’s crucial to understand what polynomials are:
- A polynomial is an expression consisting of variables (often denoted by x) and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents of variables.
- Examples include x^3 - 5x^2 + 3x + 2 or 6x - 4.
💡 Note: Polynomials can vary in complexity, but they follow a consistent pattern for operations like division.
Understanding Polynomial Division

Polynomial division is analogous to long division of integers but involves variables. Here are the basic steps:
- Set up the division problem with the dividend (the polynomial being divided) inside the division box and the divisor (the polynomial you are dividing by) outside.
- Divide the highest degree term of the dividend by the highest degree term of the divisor to get the first term of the quotient.
- Multiply the entire divisor by this term and subtract from the dividend, bringing down the next term if available.
- Repeat the process until you can no longer divide or until you have a remainder whose degree is less than that of the divisor.
📝 Note: If the remainder is 0, the divisor evenly divides into the dividend, a condition often referred to as “polynomials are evenly divisible.”
Step-by-Step Example
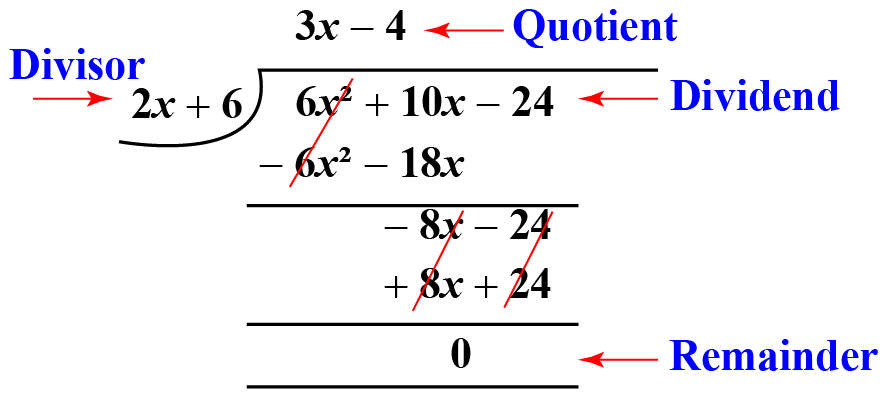
Let’s walk through an example to illustrate:
5x^3 - 3x^2 + 2x - 4 ÷ x + 2
Here’s how we proceed:
- The highest degree term of the dividend is 5x^3, and that of the divisor is x, yielding a quotient of 5x^2.
- Multiply 5x^2 by x + 2 to get 5x^3 + 10x^2, which we subtract from the original polynomial, resulting in:
- Now, divide -13x^2 by x to get -13x.
- Multiply -13x by x + 2, subtract, and repeat. Here’s the full long division:
5x^3 - 3x^2 + 2x - 4 - (5x^3 + 10x^2) = -13x^2 + 2x - 4
| Step | Operation | Result |
|---|---|---|
| 1 | 5x^3 ÷ x = 5x^2 | -13x^2 + 2x - 4 |
| 2 | -13x^2 ÷ x = -13x | 2x - 4 |
| 3 | 2x ÷ x = 2 | -8 |

Thus, the quotient is 5x^2 - 13x + 2, and the remainder is -8. The final expression can be written as:
(5x^3 - 3x^2 + 2x - 4) ÷ (x + 2) = 5x^2 - 13x + 2 - 8/(x + 2)
📚 Note: Practicing with examples is key to understanding polynomial division better.
Advanced Techniques

For complex polynomials or when simplifying results, advanced techniques can be useful:
- Synthetic Division: A shorthand method for dividing by a linear polynomial of the form x - c.
- Remainder Theorem: Useful when you only need the remainder of a division, not the quotient.
- Factoring: Sometimes, factoring can simplify the process by breaking down polynomials into simpler forms.
🎓 Note: These techniques not only expedite the division process but also deepen your algebraic understanding.
Having explored the intricacies of polynomial division, it’s time to put this knowledge into practice. Below, we’ve included a free downloadable worksheet containing problems ranging from basic to advanced polynomial division. Use it to sharpen your skills, and remember:
- Go through the step-by-step process for each problem.
- Check your answers to understand your errors.
- Try using different techniques for the same problem to see which is most efficient for you.
What is the importance of synthetic division in polynomial division?

+
Synthetic division simplifies the process when dividing by a linear divisor, making it faster and less prone to errors, especially for larger polynomials.
How do you handle negative terms in polynomial division?

+
Negative terms are treated the same as positive terms in division. They just involve changing the signs when performing the subtraction steps. It’s crucial to keep track of these changes to maintain accuracy.
Can polynomials always be divided evenly?

+
No, not all polynomials divide evenly. When they don’t, you’ll have a non-zero remainder, which can sometimes be expressed as a fraction.



