5 Simple Steps to Divide Fractions Easily

Mastering the art of dividing fractions can seem intimidating, but with the right approach, it's not only manageable but also quite straightforward. This guide aims to walk you through the process with clear steps, making you proficient in dividing fractions in no time.
1. Understanding the Basics of Fraction Division


Before diving into the steps, it’s crucial to understand what fraction division actually means. When you divide one fraction by another, you are essentially asking how many times one fraction fits into the other. It’s the same as:
- Multiplying the first fraction by the reciprocal of the second fraction.
- This turns the division into a multiplication problem, which is much easier to handle.
2. Find the Reciprocal of the Divisor

To find the reciprocal of a fraction, you need to invert the fraction:
- Turn the fraction numerator into the denominator and vice versa.
- For example, the reciprocal of 3⁄4 is 4⁄3.
3. Multiply the Numerators and Denominators
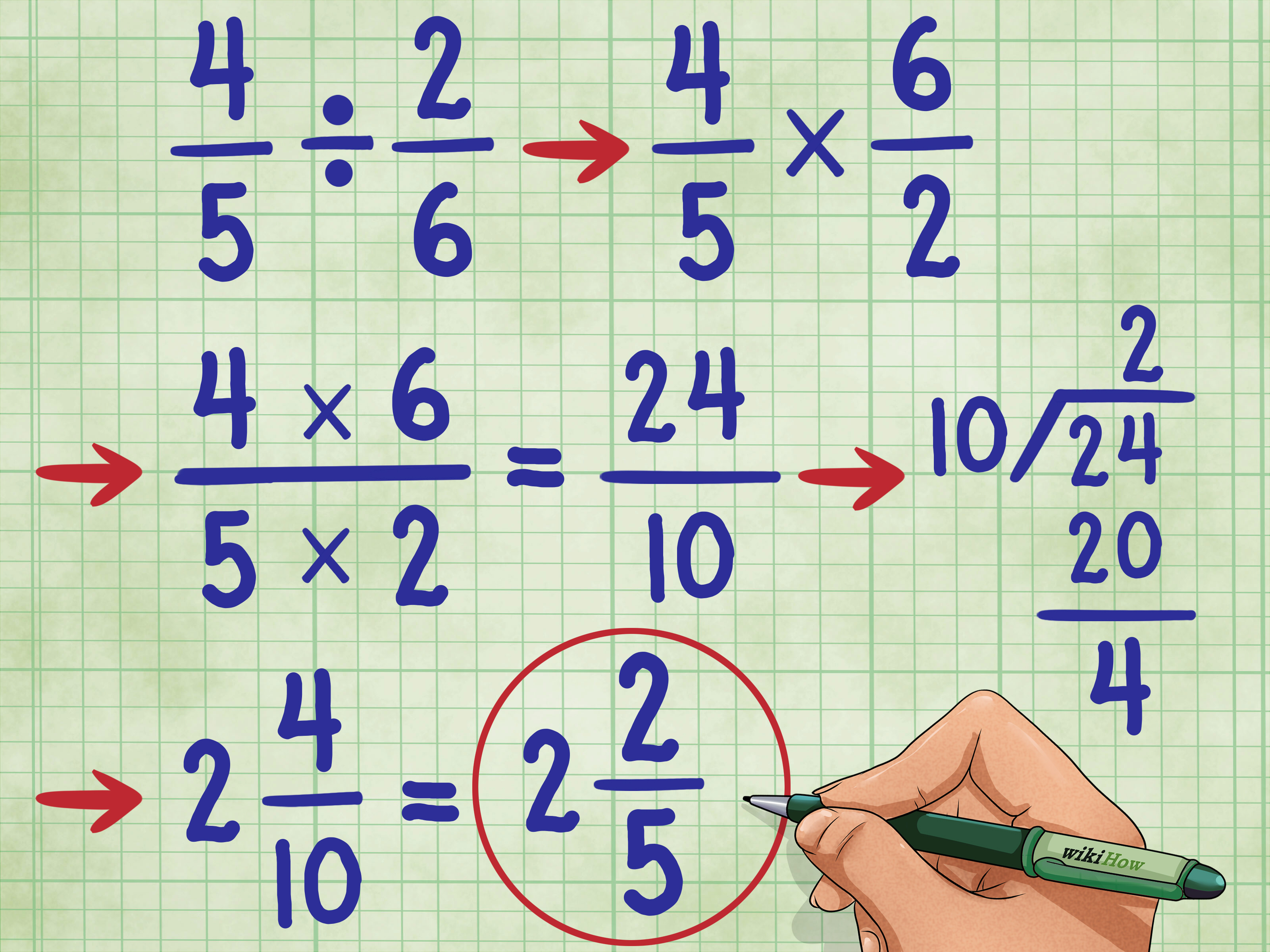
Now, with the second fraction flipped, proceed to multiply:
- Multiply the numerator of the first fraction by the numerator of the reciprocal.
- Multiply the denominator of the first fraction by the denominator of the reciprocal.
- This gives us a new fraction: (1⁄2) * (3⁄4) = (1 * 3) / (2 * 4) = 3⁄8.
4. Simplify the Fraction if Possible

After performing the multiplication, the next step is to simplify your fraction. Here’s how:
- Look for the greatest common divisor (GCD) of both the numerator and the denominator.
- Divide both parts of the fraction by this GCD.
- If no simplification is possible, your answer is already in its simplest form.
5. Practice Makes Perfect

To ensure you’ve grasped the concept, practice is key:
- Work through several examples on your own.
- Start with simple fractions and gradually increase the complexity.
- Check your answers with a calculator or online tools to ensure accuracy.
📘 Note: Practice with both whole numbers and mixed numbers to become proficient in all scenarios.
By following these steps, you've learned how to divide fractions in a methodical and easy-to-understand manner. Remember, it's about converting the problem into multiplication and then simplifying. With practice, you'll find dividing fractions to be an intuitive part of your mathematical toolkit.
Having walked through these steps, you should now feel confident in dividing fractions. Whether you're working on homework, preparing for exams, or simply engaging with mathematical concepts, the ability to divide fractions with ease will serve you well.
Why do we multiply by the reciprocal?

+
Multiplying by the reciprocal converts the division of fractions into a multiplication problem, which is simpler to solve.
How can I check if my answer is correct?

+
You can use a calculator or an online fraction calculator to verify your results.
What if the fractions cannot be simplified?

+
If the fractions have no common divisors other than 1, then your fraction is already in its simplest form.



