7 Tips for Mastering Distance on Coordinate Plane

Understanding the concept of distance on a coordinate plane is fundamental for anyone diving into geometry, navigation, or any field where spatial analysis is key. The coordinate plane, a two-dimensional space where every point is described by its x and y coordinates, offers a simple yet powerful framework for calculating distances. Here are 7 tips to master calculating distance on this plane:
1. Grasp the Distance Formula
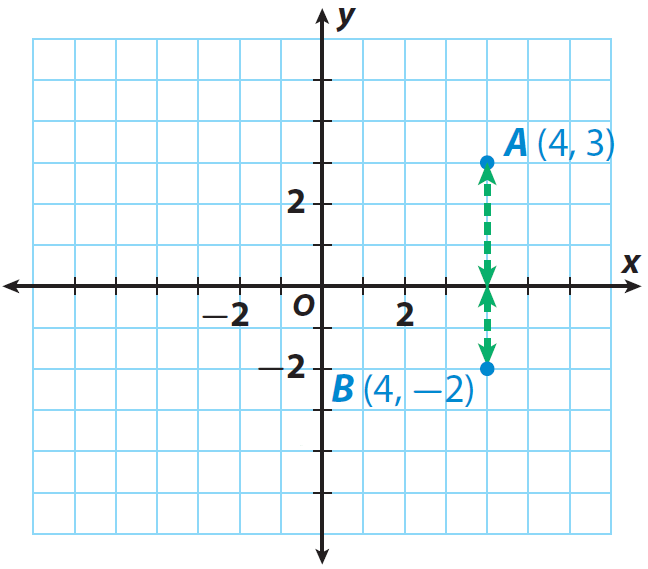

The cornerstone of measuring distances on a coordinate plane is the distance formula:
[ \text{Distance} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} ]
- x1 and y1 represent the coordinates of the first point.
- x2 and y2 are the coordinates of the second point.
Memorize this formula as it will become your go-to tool for all distance calculations.
2. Identify Coordinates Correctly

Correctly identifying the coordinates of the points on a graph or plot can prevent many errors:
- Ensure you read x-coordinate first, followed by y-coordinate.
- Double-check the signs of the coordinates to avoid mistakes with negative values.
3. Calculate Absolute Differences

Instead of subtracting x1 from x2 directly, compute the absolute difference between the coordinates. This approach helps prevent mistakes due to negative values:
[ \text{Difference in x} = |x_2 - x_1| ] [ \text{Difference in y} = |y_2 - y_1| ]
4. Utilize the Pythagorean Theorem

The distance formula is essentially an application of the Pythagorean theorem in a 2D space. Here’s how it works:
- Identify the vertical distance (|y2 - y1|).
- Identify the horizontal distance (|x2 - x1|).
- These form the legs of a right triangle, with the straight-line distance between the points being the hypotenuse.
5. Simplify the Process
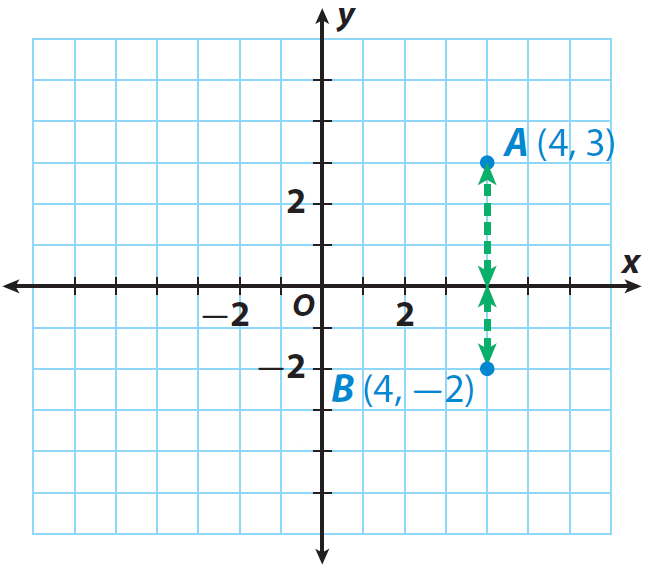
For simplicity, especially in mental calculations, consider:
- Squaring the differences in x and y directly before summing them up.
- Using a calculator or a computer application for more complex or precise calculations.
6. Visualize the Problem

Visualization can significantly enhance your understanding and calculation accuracy:
- Sketch the points on a coordinate plane if it’s not already provided.
- Draw the right triangle formed by the horizontal and vertical lines from each point.
7. Practice with Real-World Examples

| Example | Description |
|---|---|
| Traffic Navigation | Calculating the shortest path between two locations using coordinates can help avoid traffic or plan routes. |
| Surveying | Surveyors use distance calculations to map and determine land boundaries or changes in elevation. |
| Video Game Design | Developers need to calculate distances for character movements, animations, and interactions within the game environment. |

These tips should serve as a solid foundation for mastering distance on a coordinate plane. Whether you're a student, professional, or simply an enthusiast of geometry, the ability to quickly and accurately calculate distances is invaluable:
📏 Note: Always verify your calculations by plotting points or visualizing the problem to ensure accuracy.
In summary, mastering distance on a coordinate plane involves understanding the basic formula, correctly identifying coordinates, and leveraging visual aids to simplify calculations. By practicing these techniques with real-world examples, you'll find that calculating distances becomes intuitive and significantly faster, enhancing both your analytical and practical geometric skills.
What if the distance formula gives a negative result?

+
Distance in a coordinate plane is always positive. If your calculation results in a negative value, there’s likely an error in your coordinate input or calculations. The absolute value of the squared differences ensures a positive result.
Can the distance formula be used in 3D space?
+
Yes, the distance formula can be extended to three dimensions. You would calculate the distance between points by adding another term for the z-coordinates: ( \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} ).
Is it possible to calculate distances without using the distance formula?

+
Yes, you can use the Pythagorean theorem if you can draw a right triangle between the points. However, the distance formula simplifies this process by directly computing the straight-line distance without the need for constructing triangles.