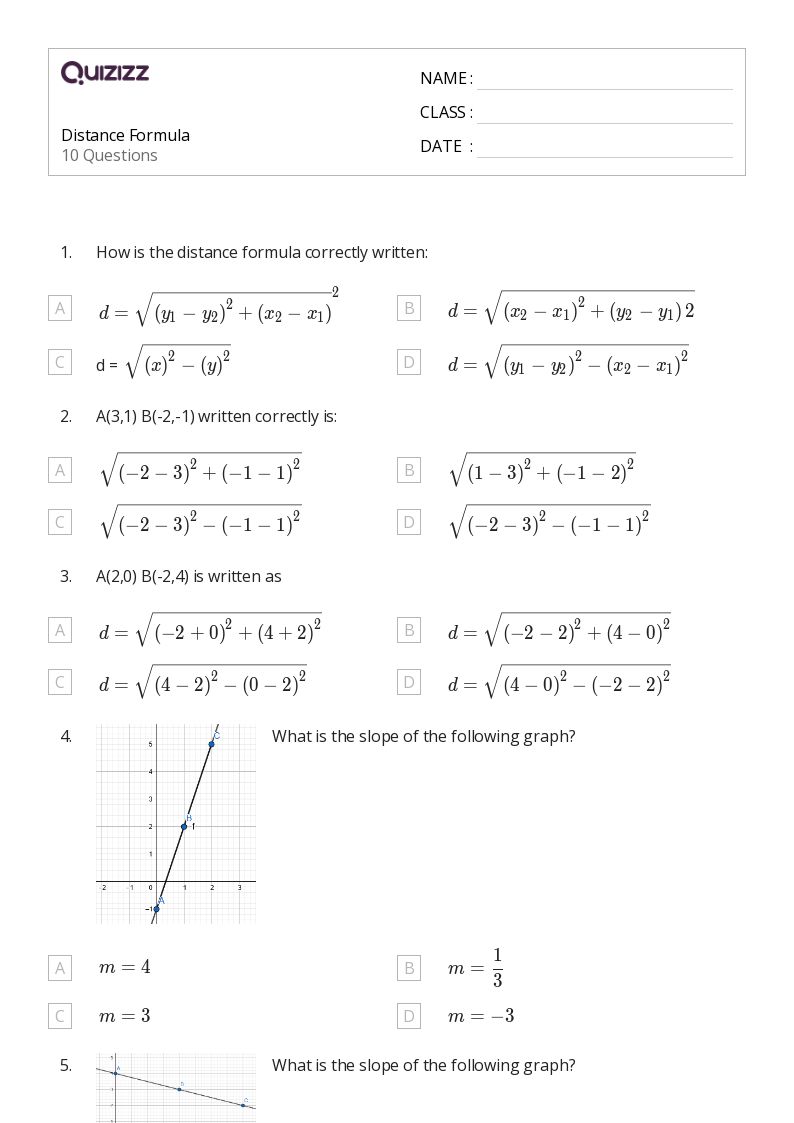
Distance Formula Worksheet Answers: Master the Equation Now

How to Master the Distance Formula: Understanding the Basics

The Distance Formula is an essential mathematical tool used to determine the distance between two points in a plane. Before we delve into its practical applications, let’s first understand its fundamental components.
What is the Distance Formula?

The distance formula is derived from the Pythagorean theorem, which states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. Here’s how it translates into the distance formula:
- Formulate: If you have two points, (A(x_1, y_1)) and (B(x_2, y_2)), the distance (d) between these two points is given by:
[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} ]
💡 Note: The formula assumes a Euclidean space, where the straight line distance between points is measured.
Steps to Solve Distance Problems
Here are the steps to use the distance formula effectively:
Identify Coordinates: Determine the coordinates of the two points you want to measure between. Label these points as (A(x_1, y_1)) and (B(x_2, y_2)).
Subtract Coordinates: Calculate the differences in the x-coordinates ((x_2 - x_1)) and y-coordinates ((y_2 - y_1)).
Square the Differences: Square both differences to remove the sign.
Add the Squares: Sum the squared differences.
Take the Square Root: Finally, apply the square root to get the actual distance.
- Example 1: Find the distance between points (3,4) and (6,8).
- Subtract coordinates: x_2 - x_1 = 6 - 3 = 3, y_2 - y_1 = 8 - 4 = 4
- Square the differences: 3^2 + 4^2 = 9 + 16 = 25
- Take the square root: \sqrt{25} = 5
Mastering Distance Formula with Examples

Now, let’s work through several examples to solidify your understanding.
Example 2: Distance in the Four Quadrants

Consider points A(-1, 3) and B(4, -5). Here’s how we can find the distance:
- Calculate (x_2 - x_1 = 4 - (-1) = 5)
- Calculate (y_2 - y_1 = -5 - 3 = -8)
- Square the differences: (5^2 + (-8)^2 = 25 + 64 = 89)
- Take the square root: (\sqrt{89} \approx 9.43)
Example 3: Non-Quadrant Points

For points like A(-7, 2) and B(5, -4):
- (x_2 - x_1 = 5 - (-7) = 12)
- (y_2 - y_1 = -4 - 2 = -6)
- Square the differences: (12^2 + (-6)^2 = 144 + 36 = 180)
- Square root of 180: (\sqrt{180} \approx 13.42)
🌟 Note: Remember to take the absolute value when calculating differences to ensure positive results.
Practical Applications of the Distance Formula

In Physics

- Trajectory Analysis: The distance formula can help in calculating the shortest path an object will travel, which is crucial in physics problems involving motion and projectile trajectories.
In Mapping and Navigation

- GPS and Location-based Services: Determining the distance between two points is vital in navigation apps for guiding users from one place to another, or for calculating distances in map-based services.
In Sports

- Field Measurements: Sports like soccer or football often require calculating distances for field strategy, player positioning, and more.
Advanced Concepts and Variations

Understanding the distance formula opens doors to more complex geometric and algebraic concepts:
- Midpoint Formula: Once you’ve found the distance, you can also find the midpoint between two points, which is given by:
[ M = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right) ]
Geometric Transformations: Knowledge of distances is essential when studying rotations, reflections, and translations.
3D Space: The distance formula extends to three dimensions, where the formula becomes:
[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} ]
Recap and Mastery

The distance formula is not just a tool for academics but a practical equation used in various real-life scenarios. Here’s a quick recap:
- Distance Formula: ( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} )
- Application: From simple geometric problems to advanced physics calculations.
- Variations: Extends to three-dimensional space, helps with midpoints, and more.
Understanding and mastering this formula allows you to navigate through more complex mathematical problems, improve your analytical skills, and apply mathematics to everyday situations effectively.
What is the importance of the distance formula in real-world applications?

+
The distance formula is crucial for navigation, engineering, physics, and even computer graphics, where the calculation of distances is necessary for determining positions, trajectories, or simulating real-world scenarios.
Can the distance formula work for negative coordinates?

+
Yes, the distance formula works with any coordinates, including negative ones. The key is to take the absolute value of the differences to ensure the result is positive.
How does the distance formula relate to the Pythagorean theorem?
+
The distance formula is derived directly from the Pythagorean theorem by imagining a right triangle where the legs are the differences in x and y coordinates, and the hypotenuse is the straight line distance between the points.