5 Must-Know Answers for Distance and Displacement Worksheet

Distance and displacement are fundamental concepts in physics, often confused by students due to their similarity in definitions yet distinct meanings. Understanding these terms is essential for grasping more complex concepts in mechanics and kinematics. In this post, we delve deep into what makes distance and displacement different, how to calculate them, and what worksheets can teach us about these two measurements.
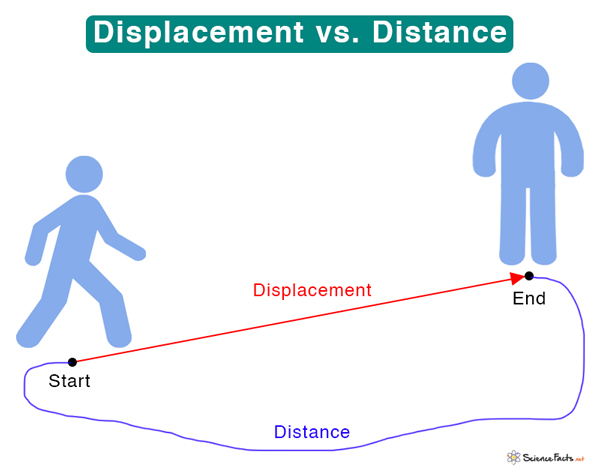
Defining Distance and Displacement

Distance refers to the total path length covered by a moving object, regardless of the direction. It is a scalar quantity, meaning it has magnitude but no direction. Conversely, displacement measures the change in position of an object, specifically the straight-line distance from the start point to the end point. Displacement is a vector quantity; it has both magnitude and direction.
How to Measure Distance

- Use an odometer for vehicular travel.
- Step counter or pedometer for human walking.
- Surveying equipment or GPS for long distances on land.
Note that the path can be curved or straight, and the only thing that matters is the total length traveled.
Calculating Displacement

- Identify the initial position and the final position of the object.
- Use vector algebra to find the displacement by considering the magnitude and direction from the initial to the final point.
📌 Note: In one-dimensional motion, displacement is simply the difference between the final and initial positions. For multi-dimensional cases, you’ll need to consider vector properties.
Worksheet Exercises for Distance and Displacement

To understand these concepts better, worksheets are invaluable tools. Here are five must-know answers to common worksheet problems:
Worksheet Problem 1

Jane walks 2 km north, then turns east and walks another 3 km. What are her total distance traveled and displacement?
- Distance: Jane traveled a total of 5 km (2 km + 3 km).
- Displacement: Using the Pythagorean Theorem, her displacement is the straight-line distance from her starting point, which is √(2² + 3²) = √13 km, or about 3.6 km northeast.
Worksheet Problem 2

A cyclist rides 10 km west and then returns half the distance to the east. What is his total distance and displacement?
- Distance: The cyclist covers 15 km in total (10 km + 5 km).
- Displacement: Since he comes back half the way, he ends up 5 km west of his starting point. The displacement is 5 km west.
Worksheet Problem 3

A hiker starts at point A, walks 3 km east to point B, then 4 km north to point C. What is her displacement from A to C?
- Displacement: The displacement here is the straight-line distance from A to C. Using the Pythagorean Theorem again, it’s 5 km northeast.
Worksheet Problem 4

If a car travels 2 km north, then 6 km west, and finally 2 km south, what is its displacement?
- Displacement: Drawing this on a graph, the displacement from the start to the end point would be 6 km west.
Worksheet Problem 5

Create a table comparing the distance traveled and displacement for various scenarios:
| Scenario | Distance (km) | Displacement (km) |
|---|---|---|
| Walk 3 km north, 3 km east | 6 | √18 ≈ 4.24 (Northeast) |
| Walk 4 km south, then 2 km north | 6 | 2 (South) |
| Walk in a circle of radius 2 km | 2π ≈ 6.28 | 0 |

In wrapping up this exploration of distance and displacement, it's clear that while both concepts are simple at their core, their application can present some fascinating challenges. The distinction between the scalar nature of distance and the vector nature of displacement often brings depth to our understanding of motion. Worksheets and practical examples like the ones discussed help solidify these concepts, allowing students to differentiate between total path length and net change in position. This not only aids in mastering mechanics but also sets a foundation for more advanced physics topics.
What’s the difference between distance and displacement?

+
Distance is the total path length traveled by an object, whereas displacement is the straight-line distance from the initial to the final position of an object. Distance is a scalar quantity with no direction, while displacement is a vector quantity with both magnitude and direction.
Why is displacement considered a vector?
+
Displacement is a vector because it measures how far and in which direction an object has moved from its starting point. It’s not just about how much ground is covered, but also about the direction in which this occurs, which is a fundamental property of vectors.
Can displacement be zero?

+
Yes, displacement can be zero if an object returns to its starting position. In such cases, the object has covered some distance, but its overall position relative to the start point remains unchanged.