5 Essential Tips for Mastering Dilation Worksheets
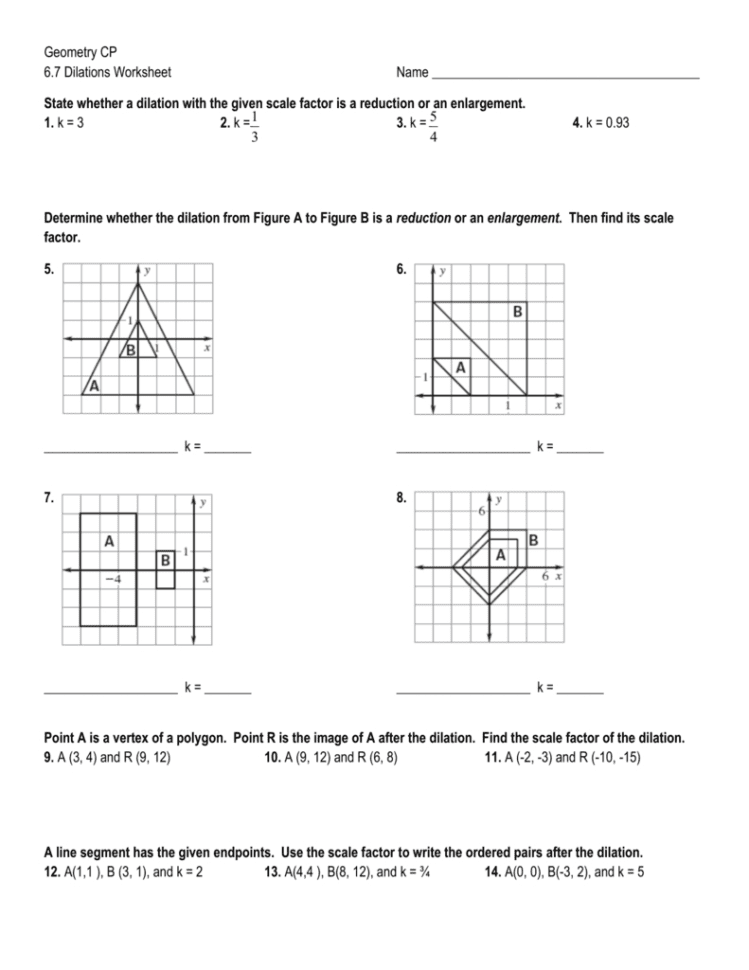
When it comes to mastering dilation worksheets in geometry, the key is understanding not just how to perform the calculations but also grasping the underlying principles that govern dilation transformations. These worksheets often come up in middle and high school curriculums, challenging students to manipulate figures in two dimensions. Here are five essential tips to help you excel at dilation worksheets:
Understand the Basics of Dilation

Before you dive into the worksheets, you must have a firm grasp of what dilation is. Dilation is a transformation that changes the size of a figure while maintaining its shape:
- Center of Dilation: This is the fixed point from which the dilation occurs. All points in the shape are moved further away from or closer to this point.
- Scale Factor: This number dictates how much larger or smaller the image will be relative to the original shape. A scale factor greater than 1 enlarges the figure, while a factor less than 1 reduces it.

🧠 Note: Dilation does not alter the shape of the figure, only its size. This is crucial for understanding your worksheets.
Use the Correct Formula

The formula for dilating a point (x, y) from a center point (a, b) with a scale factor k is:
New Point: (a + k(x - a), b + k(y - b))
When working on dilation worksheets, follow these steps:
- Identify the center of dilation and the scale factor.
- Apply the formula to each vertex of the shape to find the new coordinates.
- Connect the new points to create the dilated figure.
| Original Point | New Point (Scale Factor k = 2) |
|---|---|
| (1, 1) | (3, 3) |
| (2, 1) | (4, 3) |
| (1, 2) | (3, 4) |
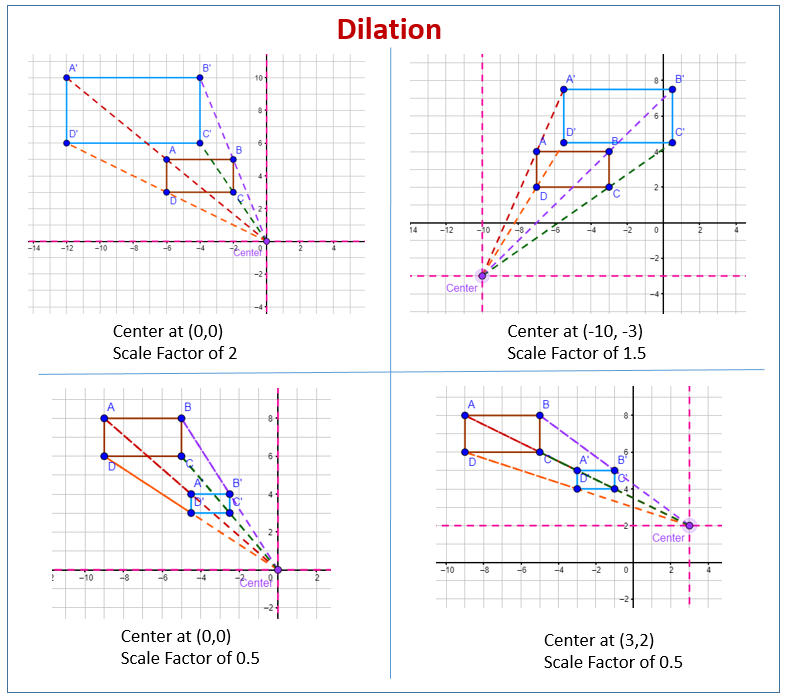
Visualize the Process

Drawing diagrams is crucial for visualizing how dilation affects a shape. Here’s how you can benefit from visualization:
- Use a pencil and grid paper or graphing software for accuracy.
- Plot the original shape and then dilate each point, connecting them to form the new image.
- Make sure the center of dilation is clearly marked, as all dilation lines will originate from this point.
💡 Note: Visualization aids understanding. Always draw out the process, even if not required by the worksheet.
Practice Dilating Different Shapes

Worksheets might include various shapes like rectangles, triangles, or even irregular polygons:
- Each shape presents unique challenges and opportunities to understand dilation better.
- Make sure to practice dilating different figures to understand how the scale factor and center of dilation affect their size and position.
👷 Note: The more varied your practice, the more adaptable you’ll become with dilation techniques.
Understand the Effects of Negative Scale Factors

Although not always covered in standard geometry classes, it’s beneficial to know:
- A negative scale factor flips the shape over the center of dilation, which can lead to unexpected but informative results.
- Understand that a negative scale factor still enlarges or reduces the shape but also reflects it through the center of dilation.
❗ Note: Negative scale factors can confuse students, so make sure you understand this concept thoroughly.
In summary, mastering dilation worksheets involves understanding the fundamentals of dilation, applying the correct formula, visualizing the process, practicing with different shapes, and exploring the effects of negative scale factors. By focusing on these key areas, you’ll develop a strong grasp of dilation transformations, enhancing your overall geometric prowess.
What is the center of dilation?

+
The center of dilation is the fixed point from which all dilation transformations occur. It remains unchanged during the transformation, and all points on the shape are either moved closer to or further away from this center.
How do I find the scale factor?

+
The scale factor can be determined by comparing the size of the dilated image to the original shape. If a side of the original shape measures 4 units and after dilation it measures 8 units, the scale factor is 2 (8 divided by 4).
Does dilation change the shape of the figure?

+
No, dilation only changes the size of the figure, not its shape. The angle measures and parallel lines remain unchanged; only the distances between points are altered.
Can the scale factor be negative?

+
Yes, a negative scale factor will still change the size of the figure but also reflect it across the center of dilation, effectively flipping the shape.
How can visualization help with dilation?

+
Visualizing helps you see the effect of dilation in real-time, allowing you to track how each point on the original figure corresponds to its new position in the dilated figure, enhancing your conceptual understanding.