5 Essential Tips for Inverse Trig Derivatives Worksheet
The world of calculus often seems daunting, filled with complex formulas and abstract concepts that can make even the most ardent math enthusiasts pause. One particularly challenging area for students is the mastery of inverse trigonometric derivatives. Understanding and applying these can greatly enhance your mathematical prowess and open doors to solving higher-level calculus problems. This article aims to break down the complexity of inverse trig derivatives, offering practical and essential tips that will guide you through worksheets and beyond.
Understanding Inverse Trig Functions

Before delving into derivatives, let’s revisit what inverse trigonometric functions are. These functions, commonly known as Arcus Functions or Anti-Trigonometric Functions, allow us to find angles based on the ratio of sides in a right-angled triangle:
- Arcsine (sin⁻¹) - Finds the angle whose sine equals the given value.
- Arccosine (cos⁻¹) - Finds the angle whose cosine equals the given value.
- Arctangent (tan⁻¹) - Finds the angle whose tangent equals the given value.
- Arccotangent (cot⁻¹) - Finds the angle whose cotangent equals the given value.
- Arcsecant (sec⁻¹) - Finds the angle whose secant equals the given value.
- Arccosecant (csc⁻¹) - Finds the angle whose cosecant equals the given value.
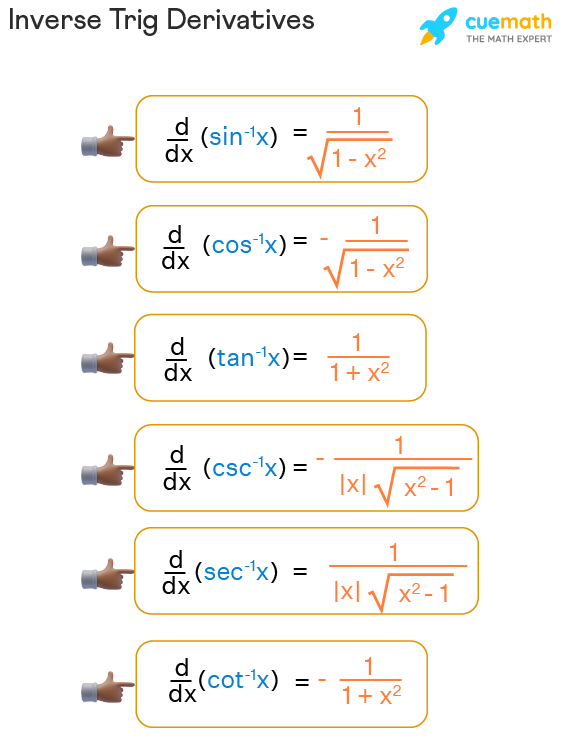
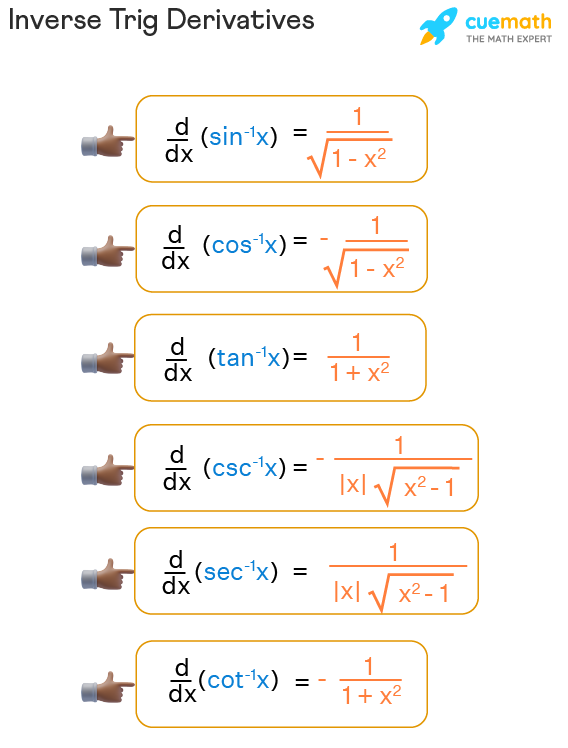
Formulas for Inverse Trig Derivatives

Once you have a grasp on what these functions represent, here are the derivatives for the main inverse trigonometric functions:
| Function | Derivative |
|---|---|
| sin⁻¹(u) | \frac{1}{\sqrt{1 - u^2}} |
| cos⁻¹(u) | -\frac{1}{\sqrt{1 - u^2}} |
| tan⁻¹(u) | \frac{1}{1 + u^2} |
| cot⁻¹(u) | -\frac{1}{1 + u^2} |
| sec⁻¹(u) | \frac{1}{u \sqrt{u^2 - 1}} |
| csc⁻¹(u) | -\frac{1}{u \sqrt{u^2 - 1}} |

Tip 1: Know the Domain and Range

Understanding the domain and range for each inverse trig function is crucial. Here’s how they differ:
- sin⁻¹(x): Domain [-1, 1], Range [-π/2, π/2]
- cos⁻¹(x): Domain [-1, 1], Range [0, π]
- tan⁻¹(x): Domain (∞, ∞), Range (-π/2, π/2)
This knowledge helps in knowing where these functions can be differentiated.
Tip 2: Transform and Manipulate

Mastery of algebra can significantly aid in manipulating derivatives of inverse trig functions:
- For composite functions like sin⁻¹(f(x)), use the chain rule: \frac{d}{dx}[sin⁻¹(f(x))] = \frac{1}{\sqrt{1 - [f(x)]^2}} \cdot f’(x)
🔔 Note: Keep in mind that algebraic manipulation can simplify complex expressions, especially when dealing with derivatives of composite functions.
Tip 3: Simplify with Substitutions

Using substitutions can simplify complex expressions:
- Set u = f(x) in the formula \frac{d}{dx}[sin⁻¹(u)] = \frac{1}{\sqrt{1 - u^2}}
🔔 Note: Substitution can be particularly effective when working with expressions involving multiple trigonometric functions.
Tip 4: Differentiation Properties

Remember these properties to simplify differentiation:
- Product Rule: [f(x) \cdot g(x)]’ = f’(x)g(x) + f(x)g’(x)
- Quotient Rule: [\frac{f(x)}{g(x)}]’ = \frac{f’(x)g(x) - f(x)g’(x)}{[g(x)]^2}
- Chain Rule: [f(g(x))]’ = f’(g(x)) \cdot g’(x)
Tip 5: Practice, Practice, Practice
Finally, the best way to understand these derivatives is through practice. Here are some suggested problems:
- Find the derivative of cos⁻¹(3x)
- Differentiate arcsin(2x + 1) with respect to x
- Calculate the derivative of tan⁻¹(x^2)
By following these tips and practicing regularly, you'll find that working with inverse trig derivatives becomes less daunting and more intuitive. Remember to keep an eye on the domains and ranges, use algebraic manipulation to your advantage, and apply the right differentiation rules to simplify and solve problems efficiently. The more you practice, the more these principles will become second nature, allowing you to tackle even the most complex calculus problems with confidence and ease.
What are the common mistakes students make with inverse trig derivatives?

+
Common mistakes include forgetting to apply the chain rule, overlooking the sign changes in derivatives like arc-cos or arc-cot, or misinterpreting the domain and range restrictions.
Why are inverse trigonometric functions important in calculus?
+
Inverse trigonometric functions are vital for solving equations involving trigonometric identities, integrating trigonometric functions, and for understanding calculus concepts like arc length and surface area of rotation.
How do inverse trigonometric functions relate to derivatives of other functions?

+
They play a crucial role in applying the chain rule, especially when you need to differentiate functions involving both trigonometric and inverse trigonometric elements. This is common in parametric equations, implicit differentiation, and related rates problems.
Can you differentiate all functions involving inverse trigonometry?

+
Not all functions involving inverse trigonometry can be differentiated everywhere due to domain restrictions. However, within their valid domains, these functions can indeed be differentiated.