Master Geometry with Deductive Reasoning Worksheets

Geometry: A Logical Approach

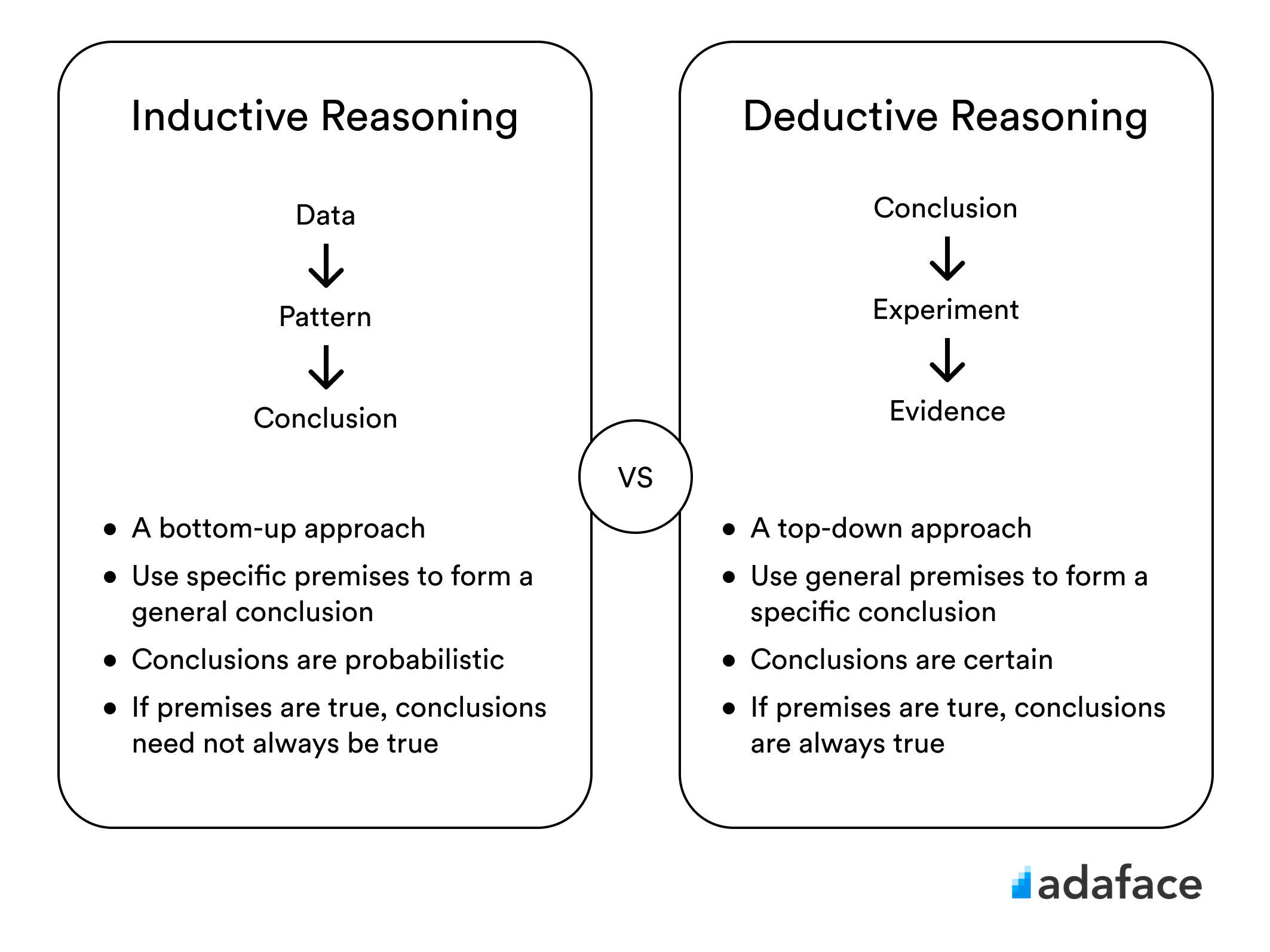
Geometry, as a branch of mathematics, isn't just about shapes and angles; it's also about logical reasoning. Deductive reasoning is a fundamental part of geometry, enabling students to make sound arguments and arrive at valid conclusions based on a set of premises. By integrating deductive reasoning worksheets into the learning process, educators can help students develop critical thinking skills while mastering the principles of geometry.

What is Deductive Reasoning in Geometry?

At its core, deductive reasoning in geometry is about drawing specific conclusions from general principles. Here are key aspects:
- General Statements or axioms act as the foundation, truths universally accepted within the field of geometry.
- Using these truths, one can deduce logical, specific conclusions by applying rules and theorems.
Benefits of Deductive Reasoning Worksheets

Worksheets designed to enhance deductive reasoning offer several benefits:
- Improved Logical Thinking: Students learn to reason from given premises to reach a conclusion, enhancing their logical thought process.
- Problem Solving: Encourages students to approach problems methodically, breaking them down into smaller, manageable parts.
- Enhanced Understanding: By working through examples, students better comprehend geometric properties and relationships.
- Precision: Students must be meticulous with their reasoning, ensuring that each step is logically sound, teaching precision in thought and expression.
How to Implement Deductive Reasoning Worksheets

Here is a step-by-step guide to effectively integrating these worksheets into geometry lessons:
1. Introduce Key Concepts

Before diving into the worksheets:
- Define deductive reasoning.
- Introduce axioms, theorems, and proofs.
- Explain the differences between inductive and deductive reasoning.
📚 Note: Ensure that students understand the basics of deductive reasoning before proceeding with complex geometric proofs.
2. Select Appropriate Worksheets

Choosing worksheets that match student's skill levels:
- Start with simpler problems for beginners.
- Gradually introduce more challenging ones involving multiple steps and properties.
3. Present Real-Life Examples

Relating geometric concepts to real-world situations helps in:
- Making the subject more engaging.
- Helping students see the practical application of geometry.
| Real-Life Example | Geometric Concept |
|---|---|
| Designing a building | Understanding of lines, angles, and shapes |
| Plotting a garden | Area, perimeter, and symmetry |

🔍 Note: Use interactive media or field trips to illustrate how geometry applies in architecture, art, and engineering.
4. Guide Students through Exercises

When working through the worksheets:
- Encourage students to write down their reasoning step-by-step.
- Promote peer review to discuss and critique each other's proofs.
5. Review and Feedback

After completing worksheets, provide:
- Immediate feedback to guide students' understanding.
- Group discussions to review common mistakes and correct misconceptions.
✅ Note: Regular review sessions can help solidify geometric concepts and reasoning skills.
Creating Your Own Deductive Reasoning Worksheets

If you prefer making your own worksheets:
- Start with simple problems and gradually increase complexity.
- Include diagrams to visualize the problem.
- Leave space for students to write their proofs.
- Incorporate a mix of multiple-choice, fill-in-the-blank, and open-ended questions.
Conclusion
In summary, deductive reasoning in geometry not only helps students to understand shapes and their properties but also cultivates a mindset geared towards logical argumentation and problem-solving. By integrating these worksheets into your curriculum, you're not just teaching geometry; you're teaching critical life skills that will serve students well beyond the classroom.
What makes a proof in geometry logically sound?

+
A proof in geometry is logically sound when it follows from universally accepted axioms or previously proven theorems, using only the rules of logical inference. Each step must be justified and directly related to the conclusion.
Can students use deductive reasoning in other subjects?

+
Absolutely! Deductive reasoning skills can be applied in science, logic, computer programming, and even in critical writing. It’s a fundamental thinking skill useful in various disciplines.
How can I motivate students who struggle with geometric proofs?

+
Relate the problems to real-life situations or use visual aids to help them understand the concepts better. Encourage them by providing easy-to-follow examples, breaking complex proofs into smaller steps, and celebrating their progress.