Cross Section Worksheets for Mastering 3D Shapes

Understanding and visualizing three-dimensional (3D) shapes can be a challenging task for many students. Whether it's in math class, architecture, or engineering, the ability to interpret 3D shapes through their two-dimensional (2D) cross-sections is a fundamental skill. This blog post delves into the importance of cross-section worksheets in education, providing insights on how they aid in mastering 3D shapes comprehension.
Why Cross Sections Matter

When we talk about 3D shapes, we often encounter terms like volume, surface area, and perimeter, but one aspect that significantly enhances understanding is the concept of cross-sections. Here’s why:
- Visualizing Interior Structure: Cross-sections provide a window into the internal structure of a 3D object, making it easier to understand complex forms.
- Intersecting Planes: They help students visualize how a 3D object interacts with an intersecting plane, revealing different shapes and dimensions.
- Problem Solving: Knowledge of cross-sections is critical for solving problems related to cutting materials, volumes, and designing structures.
Understanding Cross Section Worksheets

Cross section worksheets are designed to:
- Help students predict the shape that results from slicing a 3D figure in various directions.
- Enhance spatial reasoning skills.
- Prepare students for more advanced geometric problems in higher education.
Key Benefits of Using Cross Section Worksheets

Here are the key advantages of incorporating cross-section worksheets into the curriculum:
- Interactive Learning: Students actively participate in the learning process by drawing and analyzing cross-sections.
- Development of Problem-Solving Skills: Worksheets often present scenarios where students must figure out the appropriate cross-section.
- Application in Real Life: These exercises simulate real-world problems like slicing bread or cutting through 3D printed models.
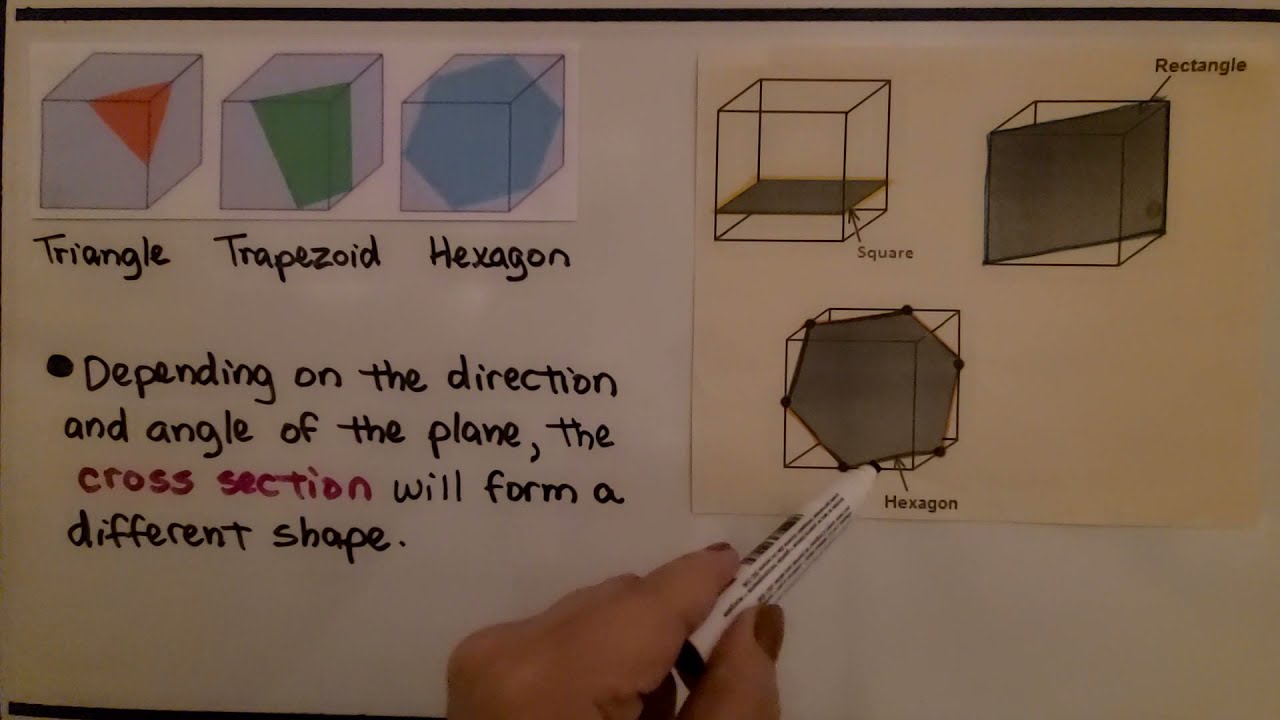
Types of Cross Sections

Let’s explore the common types of cross-sections students will encounter:
- Vertical Cross Sections: Cutting a 3D shape along a vertical plane.
- Horizontal Cross Sections: Cutting through the shape parallel to its base.
- Oblique Cross Sections: When the plane of the cut is neither vertical nor horizontal, but at an angle.
How to Approach Cross Section Problems
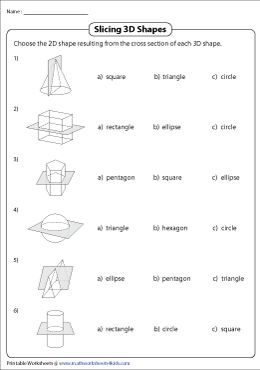
When solving cross-section problems:
- Identify the orientation of the plane (vertical, horizontal, or oblique).
- Visualize the intersection of this plane with the 3D shape.
- Sketch the resulting 2D shape.
- Calculate any necessary dimensions or properties of this shape.
💡 Note: Always start with a mental or sketched visualization to avoid confusion.
Examples and Exercises

Here are some exercises to help understand different cross-sections:
- Cube: Consider a vertical slice through the middle of a cube. The resulting shape would be a rectangle with dimensions equal to the length and width of the cube’s face.
- Cylinder: A horizontal slice through the middle would yield a circle with a diameter equal to the cylinder’s base.
Let’s visualize this through a table:
| Shape | Vertical Cross Section | Horizontal Cross Section |
|---|---|---|
| Cube | Rectangle | Square |
| Sphere | Circle | Circle |
| Cylinder | Rectangle | Circle |

Applications of Cross Sections in Various Fields

Understanding cross-sections isn’t just an academic exercise; it has numerous real-world applications:
- Architecture: Architects use cross-sections to understand building layouts and design elements like staircases and facades.
- Engineering: Engineers apply cross-section analysis when designing and analyzing structures, such as determining load-bearing capacities.
- Medicine: MRI and CT scans produce cross-sectional images to diagnose internal health issues.
- Geology: Geologists map out rock layers and understand geological structures through cross-sectional views.
🔍 Note: Different fields might emphasize different aspects of cross-sectional analysis.
Wrapping Up
In conclusion, cross-section worksheets are indispensable tools for learning and mastering 3D shapes. They bridge the gap between theoretical geometry and practical application, fostering skills that are relevant not only in education but also in various professional fields. By engaging with these exercises, students can enhance their spatial visualization, problem-solving capabilities, and critical thinking, all of which are vital for success in STEM-related disciplines.
What are the most common shapes students learn to analyze through cross sections?

+
The most common shapes include cubes, spheres, cylinders, cones, and prisms.
Can cross-section worksheets help with understanding volume?

+
Yes, by understanding the cross-section, students can better visualize how the shape changes with height, contributing to volume calculation.
How do cross-section problems relate to real-world applications?

+
Cross-section problems mirror real-world scenarios like designing structures, planning landscape, and even in medical imaging to understand interior structures.