Cross Section Of A Sphere
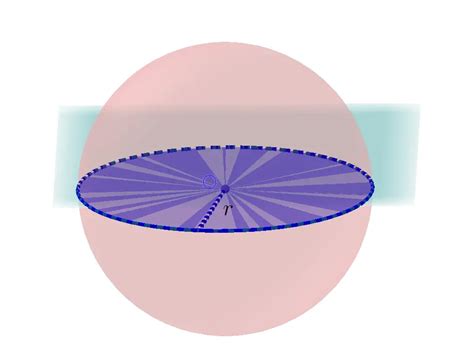
Understanding the Cross Section of a Sphere

A sphere is a three-dimensional shape that is perfectly symmetrical about its center. When a sphere is cut by a plane, the resulting intersection is called a cross section. The cross section of a sphere can take many forms, depending on the orientation and position of the cutting plane. In this article, we will explore the different types of cross sections that can be obtained from a sphere and their properties.
Types of Cross Sections
There are several types of cross sections that can be obtained from a sphere, including:
- Circular cross sections: These are obtained when the cutting plane is parallel to the diameter of the sphere. The resulting cross section is a circle, with the radius of the circle being equal to the radius of the sphere.
- Elliptical cross sections: These are obtained when the cutting plane is not parallel to the diameter of the sphere, but is still perpendicular to the axis of symmetry of the sphere. The resulting cross section is an ellipse, with the major axis of the ellipse being equal to the diameter of the sphere.
- Parabolic cross sections: These are obtained when the cutting plane is not perpendicular to the axis of symmetry of the sphere. The resulting cross section is a parabola, with the focus of the parabola being equal to the center of the sphere.
Properties of Cross Sections
The cross sections of a sphere have several important properties, including:
- Symmetry: All cross sections of a sphere are symmetrical about the center of the sphere.
- Constant curvature: All cross sections of a sphere have constant curvature, meaning that the curvature is the same at all points on the cross section.
- Perpendicularity: The cross section of a sphere is always perpendicular to the axis of symmetry of the sphere.
Applications of Cross Sections

Cross sections of spheres have many practical applications, including:
- Architecture: Cross sections of spheres are used in the design of domes and other curved structures.
- Engineering: Cross sections of spheres are used in the design of pipes and other curved pipes.
- Computer graphics: Cross sections of spheres are used in computer graphics to create realistic models of curved surfaces.
📝 Note: The cross section of a sphere can be used to create a variety of shapes and curves, making it a useful tool in many fields.
Calculating Cross Sections

The cross section of a sphere can be calculated using the following formula:
A = πr^2
Where:
Ais the area of the cross sectionris the radius of the sphere
This formula can be used to calculate the area of any cross section of a sphere, regardless of its shape or size.
Real-World Examples

Cross sections of spheres can be seen in many real-world examples, including:
- The Earth: The Earth is approximately a sphere, and its cross sections can be seen in the form of circular horizons and elliptical shadows.
- Balls: Balls, such as soccer balls and basketballs, are spheres with circular cross sections.
- Globes: Globes, such as the globe of the Earth, are spheres with circular cross sections.
Conclusion

In conclusion, the cross section of a sphere is a powerful tool that can be used to create a variety of shapes and curves. With its many practical applications and real-world examples, the cross section of a sphere is an important concept to understand in many fields.
What is a cross section of a sphere?

+
A cross section of a sphere is the intersection of a sphere with a plane. It can take many forms, including circular, elliptical, and parabolic shapes.
What are some practical applications of cross sections of spheres?
+
Cross sections of spheres have many practical applications, including architecture, engineering, and computer graphics.
How can I calculate the area of a cross section of a sphere?

+
The area of a cross section of a sphere can be calculated using the formula A = πr^2, where A is the area of the cross section and r is the radius of the sphere.
Related Terms:
- Cross section of cylinder
- Cross section of a cone
- Volume of a sphere
- Area of sphere