Cross Multiply Worksheet: Your Ultimate Math Practice Guide
In the vast and intriguing world of mathematics, techniques for solving equations stand as some of the most fundamental skills students can acquire. Among these, cross multiplication emerges as a powerful tool for swiftly solving proportions and systems of linear equations. This guide is crafted to provide you with a comprehensive Cross Multiply Worksheet to not only practice but also master this essential technique. Here, we delve into the mechanics of cross multiplication, explore real-world applications, and provide step-by-step tutorials to ensure your mathematical proficiency.
Understanding Cross Multiplication
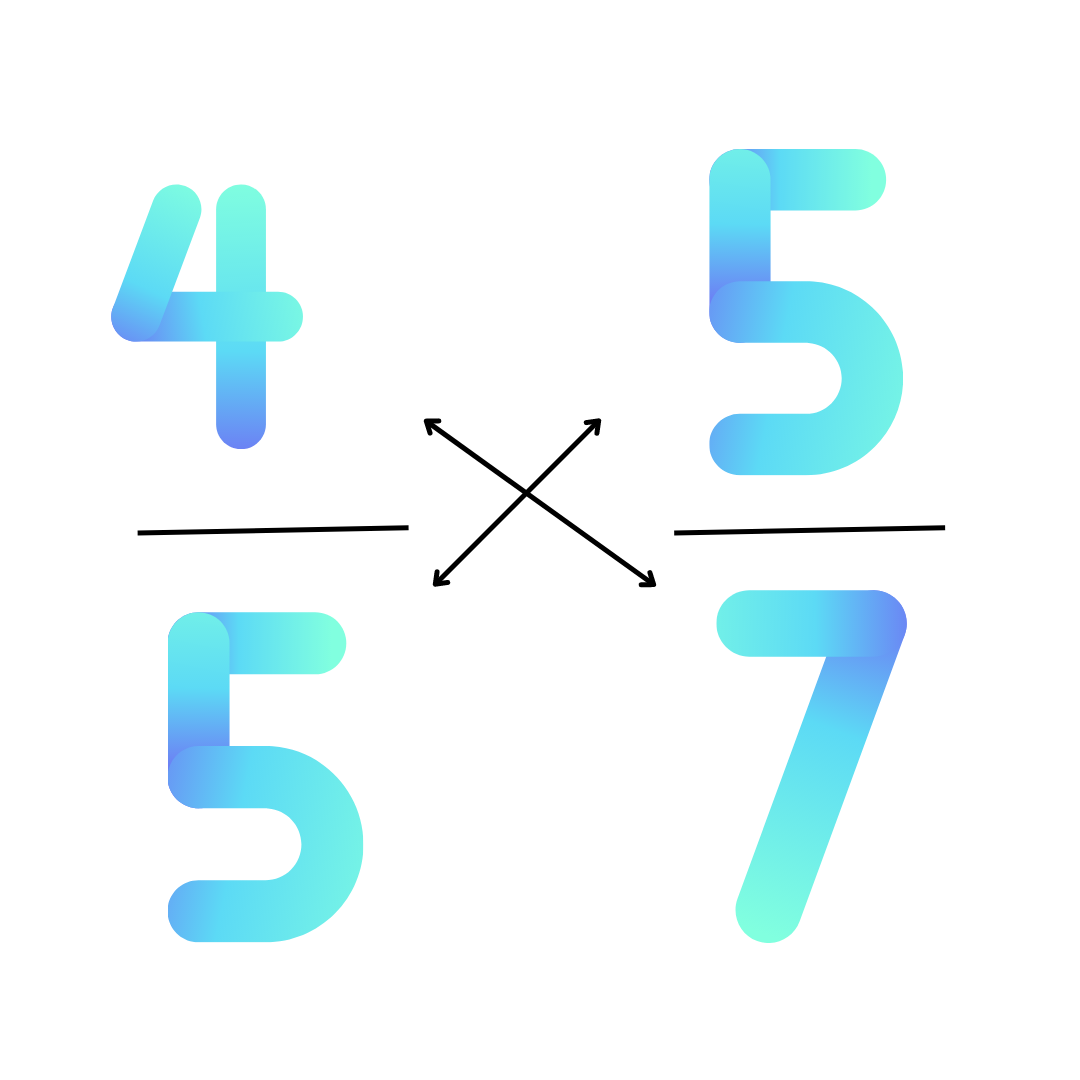
Cross multiplication is a method for solving equations with fractions or proportions. Essentially, it involves multiplying the numerator of one fraction by the denominator of the other fraction diagonally and setting the products equal to each other. Here is the basic setup:
| Setup | Process |
|---|---|
| \frac{a}{b} = \frac{c}{d} | ad = bc |

Why Use Cross Multiplication?
- Simplifies problem-solving for proportions and equations with fractions.
- Provides a clear, logical, and direct path to the solution.
- It’s versatile, applicable in algebra, geometry, and more.
Step-by-Step Guide to Cross Multiplication

Let’s break down how to apply cross multiplication effectively:
- Identify the fractions: Start with your given equation or proportion. For instance, \frac{2}{x} = \frac{3}{6}.
- Set up the cross multiplication: Multiply the numerator of the first fraction by the denominator of the second fraction and vice versa. So, 2 \times 6 = 12x.
- Solve the resulting equation: In this case, solve for x by isolating it on one side. 12x = 12, thus x = 1.
- Check your answer: Ensure your solution aligns with the original setup. Here, \frac{2}{1} = \frac{3}{6} is true.
💡 Note: Always verify the correctness of your solution to avoid any mathematical errors.
Examples in Real-World Scenarios

- Scale Model Building: When converting measurements from the model to the real-world object.
- Recipe Adjustments: Scaling up or down recipes to match serving needs.
- Finance: Calculating interest rates, exchange rates, or even investment proportions.
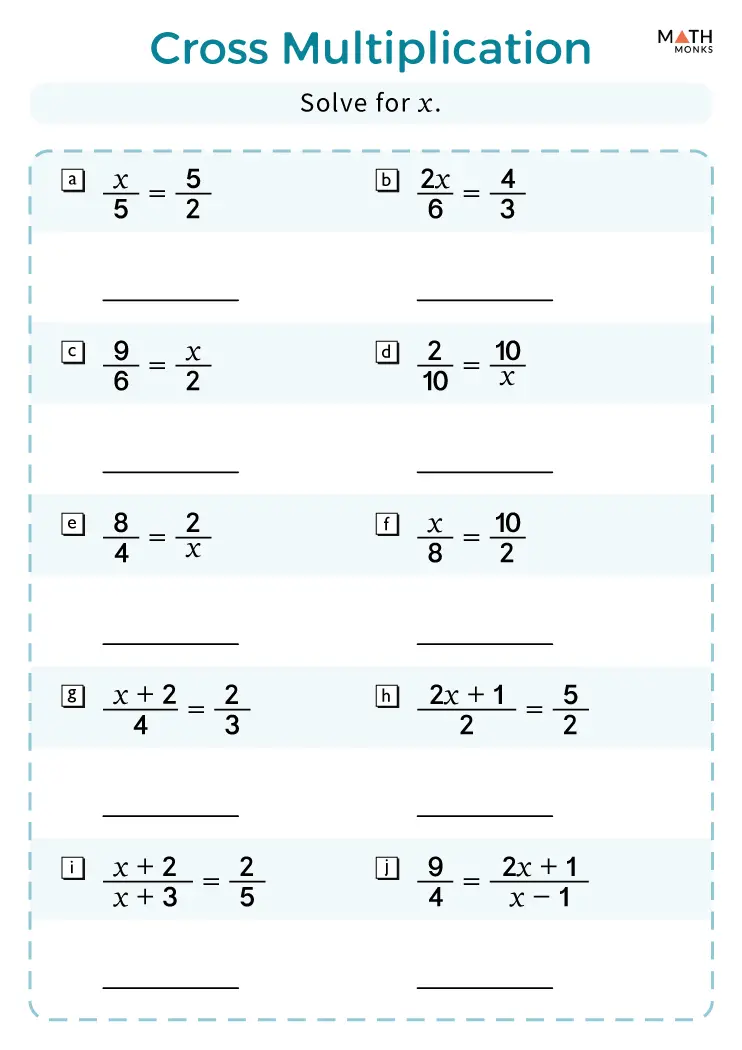
Cross Multiplication Worksheet

Below are some practice problems to help you hone your cross multiplication skills:
- \frac{4}{x} = \frac{12}{6}
- \frac{8}{3} = \frac{24}{y}
- \frac{a}{7} = \frac{16}{14}
- \frac{5}{6} = \frac{x}{12}
✅ Note: Ensure to check your work against provided solutions or even better, derive your own solutions for comparison.
Applications Beyond Basic Proportions

Cross multiplication isn’t just for simple proportions. Here are some advanced applications:
- Similar Triangles: To find missing sides in geometrically similar triangles.
- Electrical Engineering: For solving voltage dividers or determining resistance in electrical circuits.
- Economic Modeling: Calculating cost-benefit ratios or proportionality in economic models.
Final Thoughts
This guide has explored cross multiplication, from its basic mechanics to its application in everyday scenarios and beyond. Through the provided examples and practice problems, you’ve gained a comprehensive understanding of how cross multiplication functions as an essential problem-solving tool in mathematics. Whether you’re adjusting a recipe, comparing costs, or solving complex geometric problems, cross multiplication remains a steadfast ally in your mathematical toolkit. As you practice with the Cross Multiply Worksheet, remember that proficiency in this method not only boosts your speed and accuracy but also instills a deeper understanding of mathematical proportionality.
What are the common mistakes to avoid when using cross multiplication?

+
Some common mistakes include forgetting to swap the numerators and denominators correctly, confusing the operation with division, or not checking if the original proportion holds true after solving.
Can cross multiplication be applied to algebraic fractions?

+
Yes, cross multiplication can be used with algebraic fractions. The key is to multiply terms carefully and keep track of variables.
Is there a software tool to practice cross multiplication?

+
While this guide does not provide specific tools, many educational software platforms offer interactive sessions on cross multiplication, often with automated checking for immediate feedback.
Related Terms:
- Cross multiply worksheet pdf
- Free cross multiply worksheet
- Cross multiply worksheet with answers
- Cross multiply Fractions Worksheet
- Solving Equations cross multiplication corbettmaths
- Cross multiply Proportions worksheet