CPCTC Worksheet Answers Key - Simplify Geometry Proofs
Proving geometric properties often involves a series of logical steps, and CPCTC (Corresponding Parts of Congruent Triangles are Congruent) is a pivotal theorem in simplifying these proofs. This blog post dives into the details of CPCTC, offers a structured worksheet, and provides answers to common problems, helping you to master the art of simplifying geometry proofs.
Understanding CPCTC

CPCTC is a principle used after establishing the congruence of two triangles. It states that if two triangles are congruent, then their corresponding parts (angles and sides) are congruent as well. Here’s how you can effectively use CPCTC:
- Identify Congruent Triangles: First, prove that two triangles are congruent using one of the triangle congruence postulates or theorems (SSS, SAS, ASA, AAS, or HL).
- Apply CPCTC: Once congruence is established, use CPCTC to assert that corresponding parts of these triangles are equal.
The CPCTC Worksheet: A Practical Approach

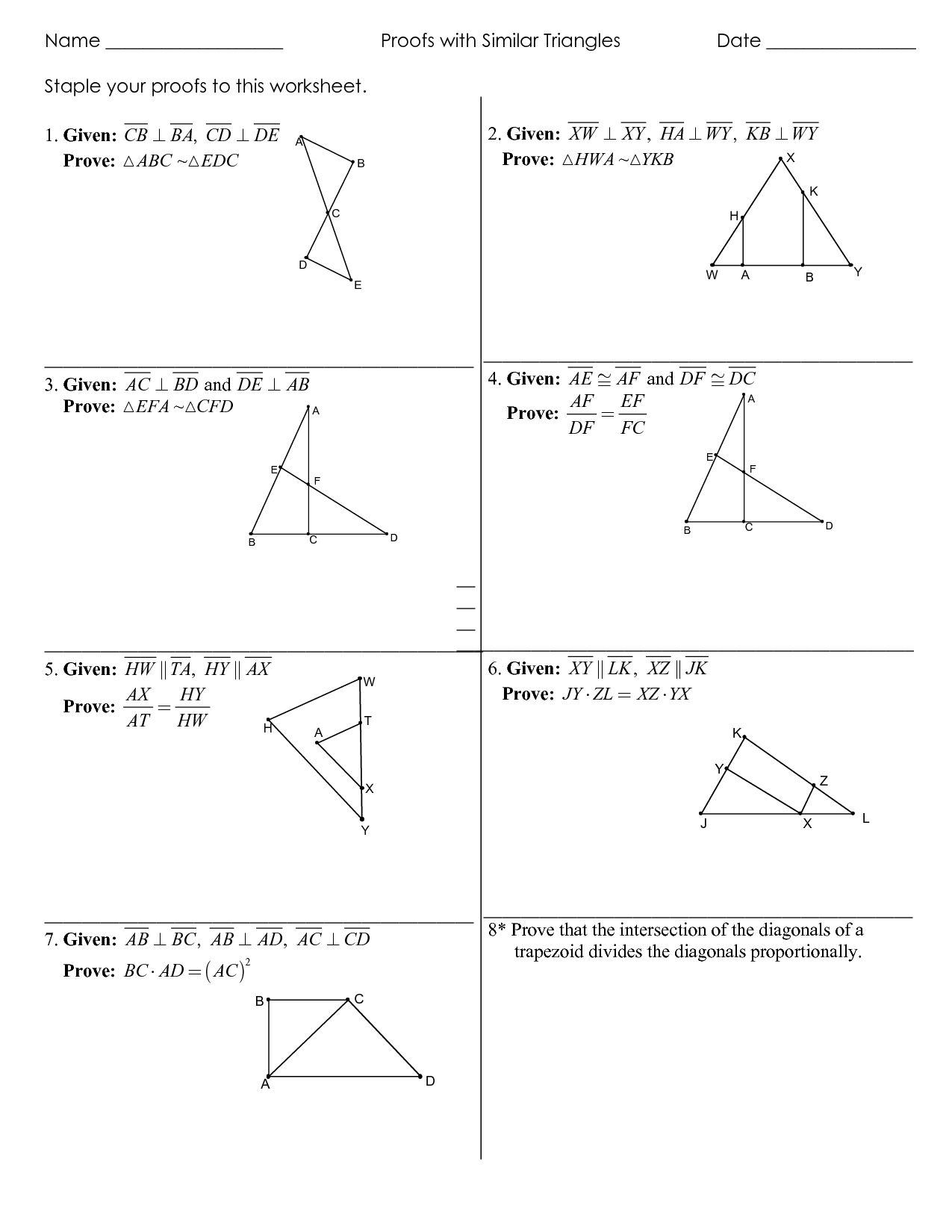
Below is a worksheet designed to enhance your understanding and application of CPCTC in geometry proofs:
| Problem | Solution |
|---|---|
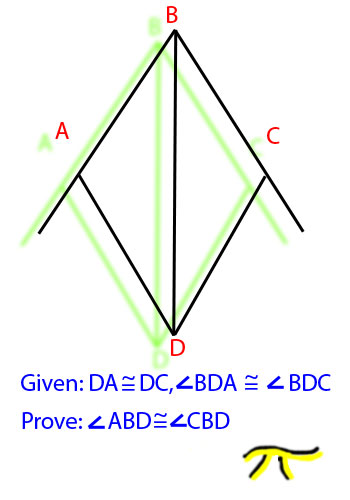
| Given: AB ≅ CD, AD ≅ BC Prove: ∠A ≅ ∠C |
Proof Steps:
|
| Given: △ABC ≅ △DEF, BC ≅ EF Prove: ∠A ≅ ∠D |
Proof Steps:
|

🔍 Note: Always make sure to clearly state which congruence postulate or theorem you use when proving triangles are congruent before applying CPCTC.
CPCTC in Real-Life Geometry Problems

CPCTC isn't just an abstract theorem; it has practical applications in real-world geometry problems. Here are some examples:
- Bridge Design: Engineers use geometric proofs to ensure that bridge structures are symmetrical and structurally sound.
- Construction: Accurate measurement and congruence of parts are crucial in building precise structures like frameworks or supports.
Key Takeaways
To maximize the benefits of CPCTC:
- Remember that CPCTC is only used once triangles are proven congruent.
- CPCTC can be used to prove congruence of angles, sides, or even to establish isometry in figures beyond triangles.
- Mastering CPCTC will significantly simplify many geometry proofs, making them more straightforward and easier to understand.
With this knowledge, the journey through geometry becomes less daunting, turning complex proofs into manageable steps through the power of CPCTC.
Why can’t CPCTC be used as a reason to prove triangle congruence?

+
CPCTC is a consequence of triangle congruence, not a method to prove it. It’s used after you’ve already established that two triangles are congruent using one of the triangle congruence postulates or theorems.
Can CPCTC be used in proofs involving more than two triangles?

+
Yes, CPCTC can be extended to prove the congruence of parts in multiple triangles if each pair of triangles is shown to be congruent first.
What are common mistakes students make when using CPCTC?

+
Common mistakes include:
- Using CPCTC without first proving triangle congruence.
- Confusing which corresponding parts are congruent.
- Failing to label diagrams correctly, leading to confusion in proof steps.