5 Proven Methods for Mastering CPCTC Proofs Easily

Geometry, often considered an intricate field of mathematics, can be demystified through strategic learning techniques. A particularly challenging area for many students is the proofing method known as CPCTC or Corresponding Parts of Congruent Triangles are Congruent. This method, while fundamental to understanding geometric congruence, requires a thorough understanding and careful application of several key principles. In this comprehensive guide, we'll explore five proven methods that can significantly simplify the process of mastering CPCTC proofs.
Understanding CPCTC

Before diving into the methods, let’s clarify what CPCTC entails. CPCTC is a theorem used in geometry to show that if two triangles are congruent, then their corresponding parts (angles or sides) are also congruent. Here’s a quick breakdown:
- Two triangles are congruent if all corresponding sides and angles are equal.
- Once congruence is established, CPCTC allows us to claim that any pair of corresponding parts are equal.
- The statement follows the format: “Since Triangle ABC is congruent to Triangle DEF, then AB = DE, BC = EF, CA = FD, angle A = angle D, angle B = angle E, and angle C = angle F.”
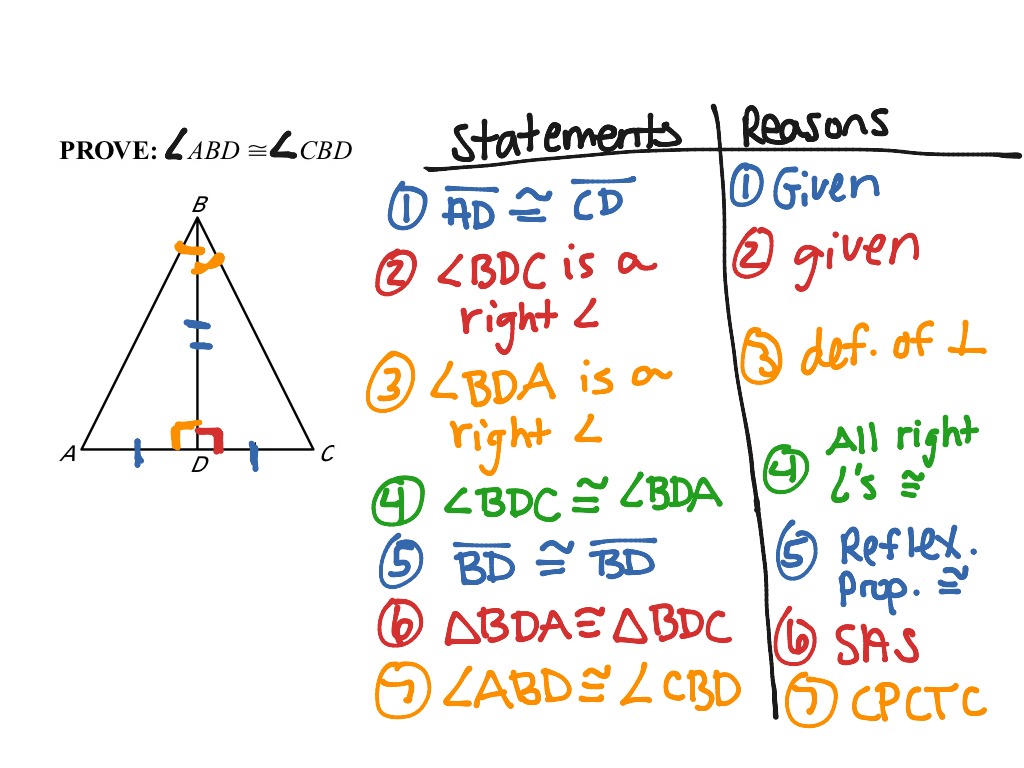
Method 1: Diagramming Your Thoughts

Visual aids can dramatically reduce the complexity of geometric proofs.
- Draw Accurate Diagrams: Always begin with a clear, accurate diagram of the given information. Use a ruler, compass, or geometry software to ensure precision.
- Label Everything: Mark all given information, including sides and angles, on the diagram. This visual representation helps in seeing the congruence more easily.
- Use Dotted Lines: If there are potential auxiliary lines or segments that can help in proving congruence, draw these with dotted lines to keep the diagram organized but informative.
💡 Note: Even if a diagram isn’t given in the problem, drawing one can clarify relationships between elements that might not be immediately obvious in the text.

Method 2: Focused Postulate Review

Understanding and memorizing the postulates that lead to triangle congruence is crucial:
- SSS (Side-Side-Side): Three sides of one triangle are equal to three sides of the other triangle.
- SAS (Side-Angle-Side): Two sides and the included angle of one triangle are congruent to two sides and the included angle of the other.
- ASA (Angle-Side-Angle): Two angles and the included side of one triangle are congruent to two angles and the included side of another.
- AAS (Angle-Angle-Side): This is equivalent to ASA, but one of the angles is not included between the sides.
- HL (Hypotenuse-Leg) for right triangles: If the hypotenuse and one leg of one right triangle are congruent to the hypotenuse and one leg of another right triangle.
Regularly practicing these postulates will sharpen your ability to quickly identify the path to proving triangles congruent.
Method 3: Flowchart Proofs

Flowchart proofs provide a visual roadmap for proofing, which is especially helpful with CPCTC:
| Statement | Reason |
|---|---|
| AB = DE, BC = EF, AC = DF | Given |
| Triangle ABC is congruent to Triangle DEF | SSS |
| angle BAC = angle EDF, angle ABC = angle DEF, angle ACB = angle DFE | CPCTC |

The flowchart allows you to:
- See the logical progression of your proof.
- Backtrack if needed, ensuring no steps are missed or wrongly stated.
- Understand the interconnections between statements and postulates.
Method 4: Use Auxiliary Elements

Sometimes, adding auxiliary lines or points can reveal congruence that is not immediately apparent:
- Draw perpendiculars to non-parallel sides to find congruent segments.
- Extend sides or draw auxiliary triangles to meet congruence conditions.
- Use midpoints to create congruent triangles through the midpoint theorem.
✅ Note: The addition of auxiliary elements should always be justified by geometric principles, not mere convenience.
Method 5: Rehearse with Real-world Scenarios

Geometry, like any math subject, benefits from real-world application:
- Use blueprints or architectural plans to identify CPCTC proofs in building structures.
- Practice with landscaping and surveying where exact dimensions must be congruent.
- Examine mechanical parts of machinery where parts must be precisely cut or manufactured to fit.
These scenarios help in:
- Understanding the practical significance of CPCTC.
- Enhancing spatial reasoning, which is integral to geometric proofs.
- Recognizing patterns and congruence in real life, making abstract concepts more concrete.
In conclusion, mastering CPCTC proofs involves understanding the underlying principles, practicing with various methods, and applying them in real-world contexts. By employing these five proven strategies—diagramming your thoughts, reviewing postulates, using flowchart proofs, adding auxiliary elements, and practicing with real-life scenarios—you can make the complex task of proving triangle congruence simpler and more intuitive. The process of learning and applying CPCTC not only enriches your geometric knowledge but also enhances your logical and spatial reasoning skills, crucial for mathematical problem-solving at any level.
How often should I practice CPCTC proofs to master them?
+
Consistency is key. Practicing at least once or twice a week with varied problems will help solidify your understanding. However, daily practice, even if brief, is even better.
Can CPCTC be applied to non-triangular shapes?

+
CPCTC is specifically for triangles since the theorem is about congruent triangles. For other polygons, similar principles exist, but different congruency postulates are applied.
What’s the difference between CPCTC and the Congruence Postulates?

+
Congruence postulates (like SSS, SAS, ASA, etc.) establish that triangles are congruent. CPCTC is used after the triangles are proven congruent to assert that their corresponding parts are equal.