Coulomb's Law Worksheet Answer Key Revealed: Master Physics Now

Coulomb's Law is a fundamental principle in physics that deals with the electric force between charges. Understanding Coulomb's Law is crucial for students of physics, as it not only helps in grasping basic electrostatic interactions but also serves as a foundation for deeper explorations into electromagnetism. This blog post will delve into an answer key for a worksheet on Coulomb's Law, providing insights and explanations to help you master this essential physical law.
What is Coulomb's Law?

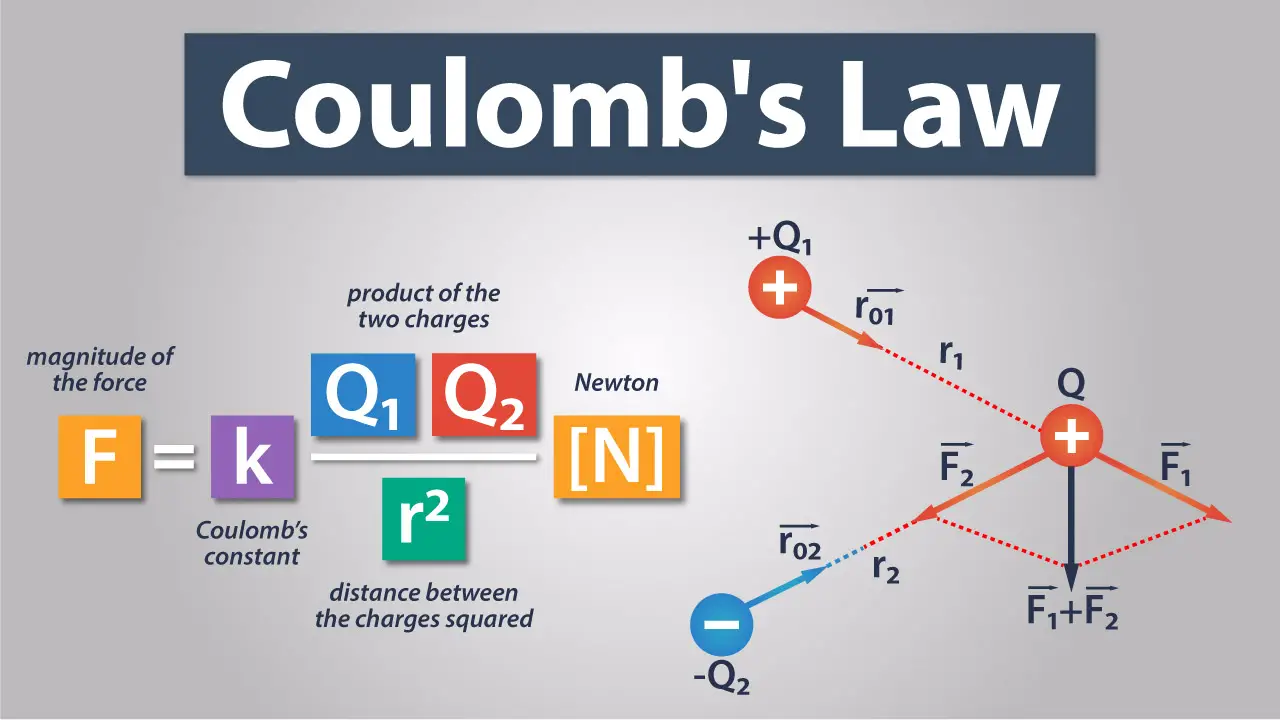
Coulomb's Law expresses the force between two point charges:
- Force (F): This is the electric force between the charges.
- Charge 1 (q1) and Charge 2 (q2): These are the two point charges interacting.
- Distance (r): The distance between the centers of the charges.
- Coulomb's Constant (k): This is a proportionality factor given by k = 8.99 \times 10^9 \, N \cdot m^2/C^2 .
The law can be mathematically represented as:
\[ F = k \frac{|q_1 q_2|}{r^2} \]
⚡ Note: The force direction is determined by the charges' signs, where like charges repel and unlike charges attract.
Analyzing Coulomb's Law Worksheet Problems

Problem 1: Force Calculation

Calculate the force between two charges of 3 \, \mu C and -5 \, \mu C when placed 2 meters apart.
| Charge 1 (q1) | Charge 2 (q2) | Distance (r) | Force (F) |
| 3 μC | -5 μC | 2 m | 1.67 × 10-2 N |
To solve:
- Use the equation F = k \frac{|q_1 q_2|}{r^2}
- Plug in the values: \[ F = (8.99 \times 10^9 \, N \cdot m^2/C^2) \frac{3 \times 10^{-6} \, C \times 5 \times 10^{-6} \, C}{2^2} \] \[ F = 1.67 \times 10^{-2} \, N \]
Problem 2: Distance Calculation

Determine the distance at which two charges of 1 \, \mu C would exert a force of 1 \, N on each other.
| Charge 1 (q1) | Charge 2 (q2) | Force (F) | Distance (r) |
| 1 μC | 1 μC | 1 N | 8.99 × 10-2 m |
Solution:
- Rearrange the formula: \[ r = \sqrt{\frac{k \cdot q_1 \cdot q_2}{F}} \]
- Plug in the values: \[ r = \sqrt{\frac{(8.99 \times 10^9 \, N \cdot m^2/C^2) \times 1 \times 10^{-6} \, C \times 1 \times 10^{-6} \, C}{1 \, N}} \] \[ r \approx 8.99 \times 10^{-2} \, m \]
Problem 3: Change in Charge Magnitude

How does the electric force change if the magnitudes of the charges are doubled?
The force increases by a factor of 4 .
Explanation:
- The force depends on the product of the charges: F \propto |q_1 q_2| .
- When both charges are doubled: F' = k \frac{(2q_1)(2q_2)}{r^2} = 4 k \frac{q_1 q_2}{r^2} = 4F .
Problem 4: Inverse Square Law

If the distance between two charges is halved, what happens to the force?
The force increases by a factor of 4 .
Explanation:
- The force varies inversely with the square of the distance: F \propto \frac{1}{r^2} .
- When distance is halved: F' = k \frac{|q_1 q_2|}{(r/2)^2} = k \frac{|q_1 q_2|}{\frac{r^2}{4}} = 4k \frac{|q_1 q_2|}{r^2} = 4F .
Mastering Coulomb's Law

Through this detailed examination of Coulomb's Law worksheet problems, we've covered several key aspects:
- Calculation of the electric force between charges.
- Determining how changes in charges or distances affect this force.
- Understanding the mathematical relationships involved in Coulomb's Law.
By practicing these types of problems, you will develop a deeper understanding of how charges interact, which is vital not just for academic success but also for practical applications in electrical engineering, materials science, and more. Keep in mind the inverse square law and how force magnitude changes with charge variations. This knowledge will serve as a robust foundation for tackling more complex electromagnetic phenomena in the future.
What units should I use for Coulomb’s Law calculations?

+
For Coulomb’s Law, use charges in coulombs ©, distances in meters (m), and the force will be calculated in Newtons (N).
Why is Coulomb’s Law important?

+
Coulomb’s Law is fundamental in understanding the interactions between charged particles, which underpins electromagnetism, one of the four fundamental forces in nature.
How do I remember the direction of force in Coulomb’s Law?

+
Remember that like charges (both positive or both negative) repel each other, and unlike charges (one positive, one negative) attract each other.