5 Tips for Mastering Coordinate Planes Quickly
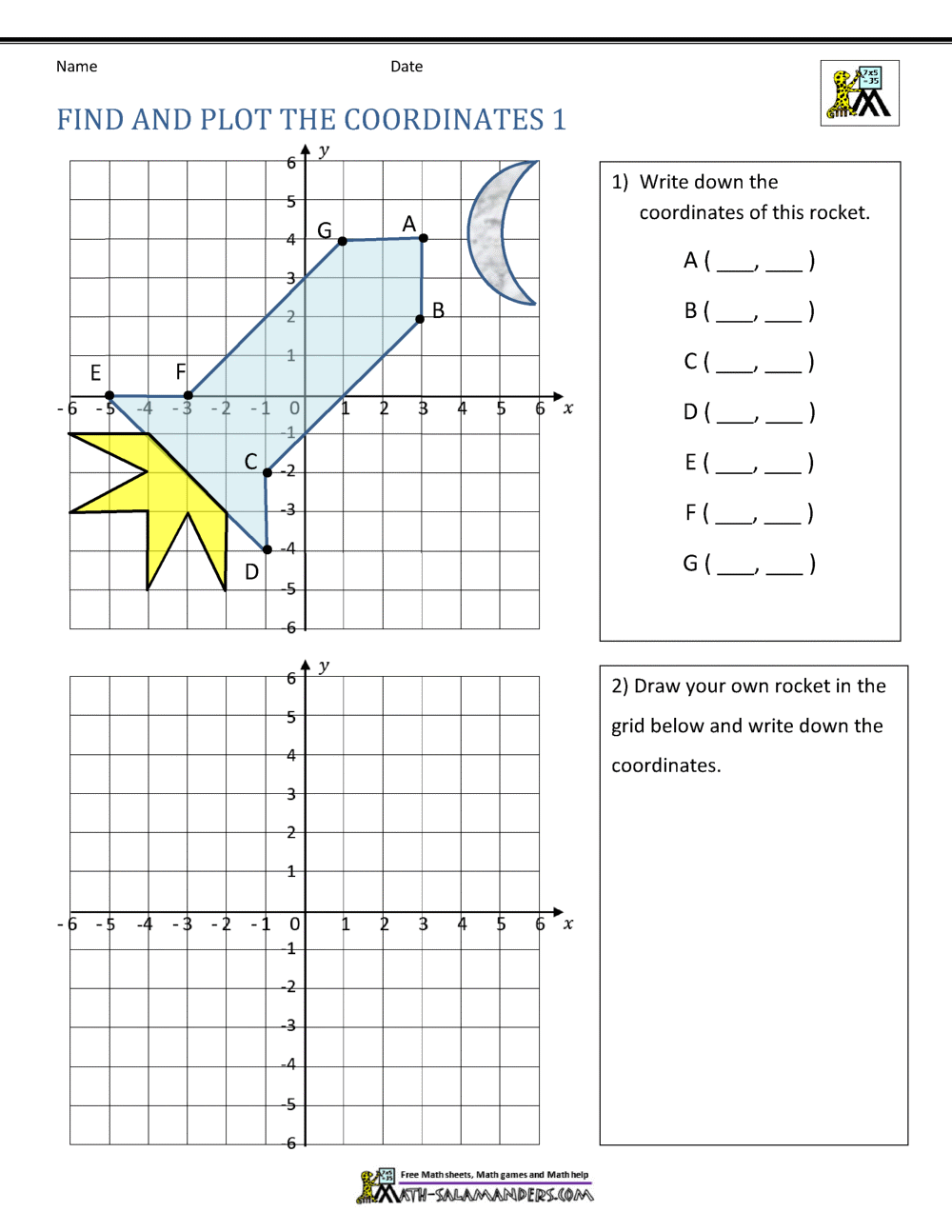
Understanding and mastering the coordinate plane is crucial for a range of applications, from basic mathematics and engineering to advanced areas like computer graphics and navigation systems. Here are five expert tips to help you swiftly become adept at navigating and utilizing the coordinate plane effectively.
Visualize Axes and Key Points

One of the first steps to mastering the coordinate plane is to visualize its fundamental components:
- The horizontal line or the x-axis where y=0.
- The vertical line or the y-axis where x=0.
- The origin, the intersection point of both axes where x=0 and y=0.
Spend time visualizing these basic elements. Imagine or sketch out the grid with increasing and decreasing values along both axes. Understand that every point on this plane has two numbers associated with it - the x-coordinate and the y-coordinate.
💡 Note: This visualization will help in understanding directions (like moving right or left on x, up or down on y), distances, and relative positions of points.
Master the Art of Plotting Points

Plotting points on a coordinate plane is more than just marking a point:
- Start from the origin.
- Move along the x-axis to find the x-coordinate.
- Then, move up or down along the y-axis to find the y-coordinate.
- Mark the point where these two movements intersect.
Here is an example:
| Coordinate | Steps to Plot |
|---|---|
| (3, 4) | Move 3 units right, then 4 units up from the origin. |
| (-2, 0) | Move 2 units left along the x-axis, staying on the x-axis since y=0. |

Practice this until it becomes second nature.
Understand Quadrants and Their Signs

The coordinate plane is divided into four quadrants, each with unique characteristics:
- Quadrant I - Both x and y are positive. Coordinates like (2, 3) belong here.
- Quadrant II - x is negative, y is positive. Coordinates like (-1, 4).
- Quadrant III - Both x and y are negative. Coordinates like (-2, -3).
- Quadrant IV - x is positive, y is negative. Coordinates like (3, -2).
Knowing which quadrant a point is in instantly tells you the sign of its coordinates, speeding up calculations and plotting.
Use Geometric Formulas
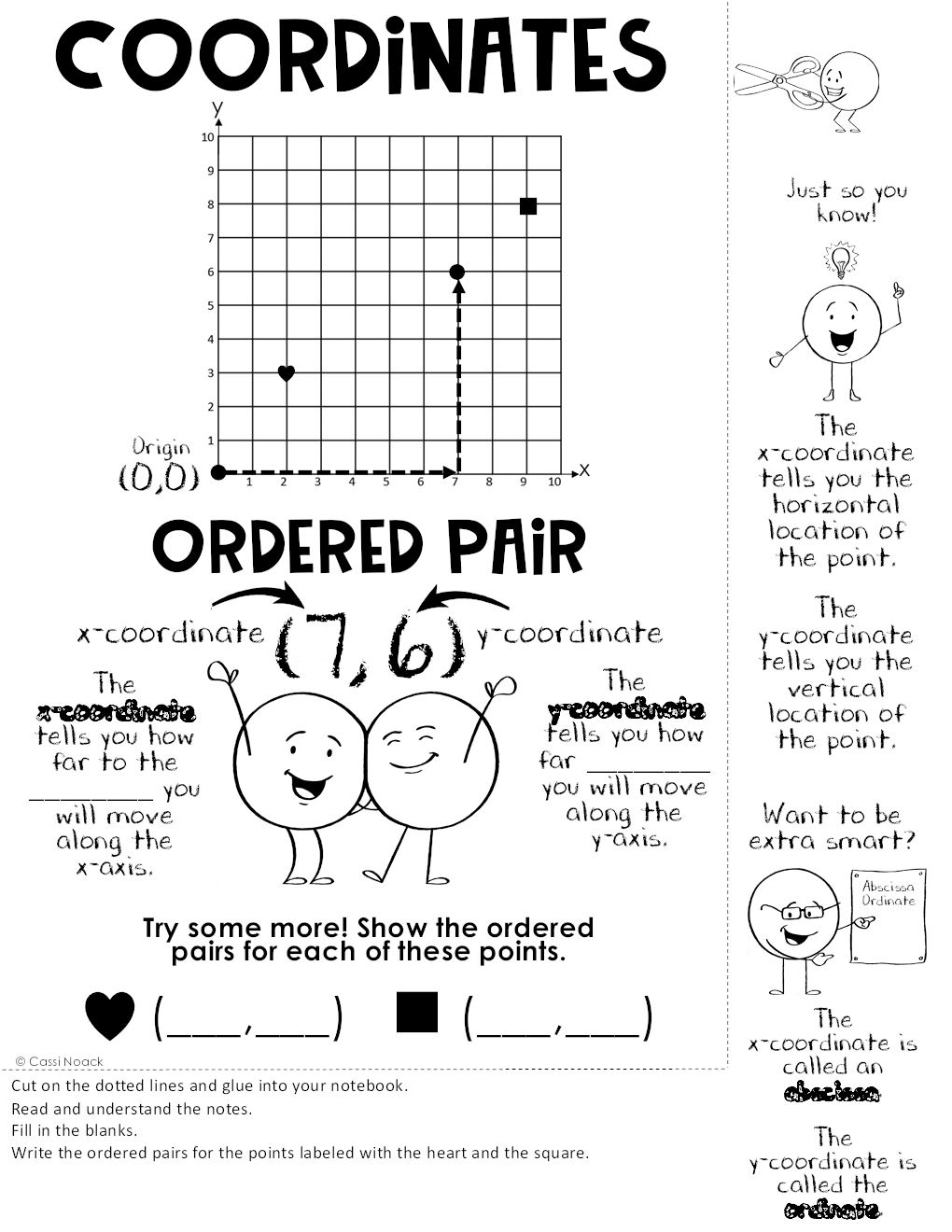
Once you’ve grasped the basics of plotting, delve into the following geometric relationships:
- Distance Formula: √((x2-x1)^2 + (y2-y1)^2) - used to find the distance between two points.
- Midpoint Formula: ((x1+x2)/2, (y1+y2)/2) - to find the midpoint of a line segment.
- Slope Formula: (y2-y1)/(x2-x1) - gives the slope of a line passing through two points.
These formulas provide a deeper understanding and can be applied in real-world problems like calculating distances in maps or finding slopes in road construction.
Practice with Real-world Applications

Finally, reinforce your mastery by applying coordinate geometry to everyday scenarios:
- Navigate using maps where coordinates can represent locations or landmarks.
- Engage in computer graphics where the screen is essentially a coordinate plane.
- Understand the movement of objects in physics simulations.
Practical application not only cements your understanding but also makes learning more engaging.
🔍 Note: The more you practice with real-world scenarios, the better you’ll understand the relevance and utility of the coordinate plane.
In summary, to quickly master coordinate planes, start by visualizing axes and key points, master plotting points, understand quadrants, apply geometric formulas, and engage with real-world applications. These five tips will not only boost your understanding of coordinate geometry but also prepare you for advanced topics where spatial reasoning is crucial. The combination of visualization, practice, and application will make navigating the coordinate plane a breeze.
Why is it important to visualize the coordinate plane?

+
Visualizing the coordinate plane helps in understanding directions, distances, and relative positions of points, making it easier to plot points and understand complex geometric relationships.
How can plotting points be improved?

+
By mastering the steps to plot points and practicing with different coordinate values, one can improve their accuracy and speed in plotting points on the coordinate plane.
What are the practical applications of understanding quadrants?

+
Knowing quadrants helps in quickly identifying the signs of coordinates, which is useful in navigation systems, computer graphics, and various scientific and engineering calculations.