Effortless Guide: Percents to Decimals Conversion Worksheet
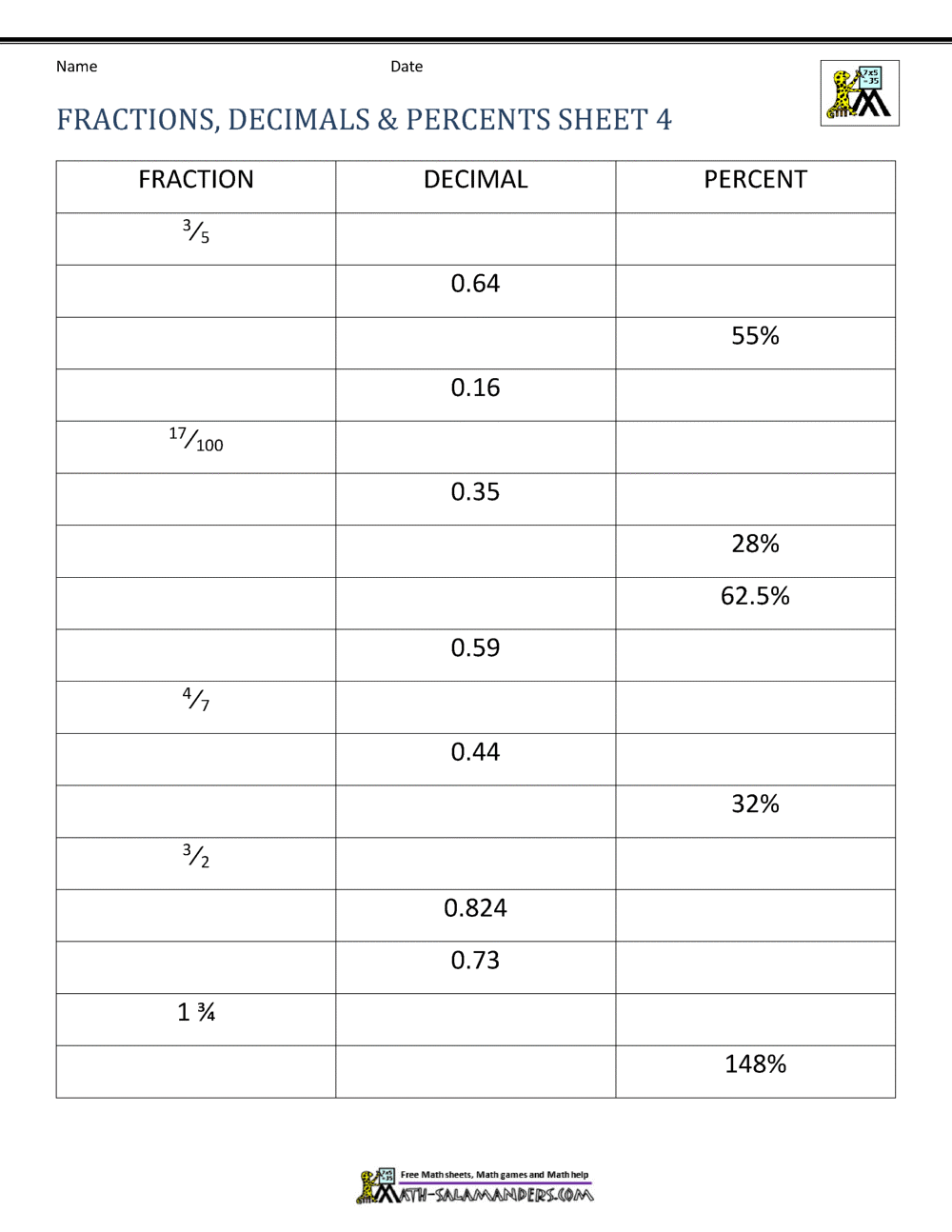
Have you ever been faced with the task of converting percentages to decimals and found yourself unsure of where to start? Percentages are a common part of our daily mathematical interactions, but understanding how to seamlessly switch between them and their decimal equivalents is an essential skill that can simplify a variety of calculations. Let's delve into a straightforward guide on converting percents to decimals, complete with practical examples and a worksheet for practice.
Understanding Percentages and Decimals

Before we start converting, it’s helpful to grasp the relationship between percentages and decimals. A percentage is essentially a way to express a number as a fraction of 100. When we convert a percentage to a decimal, we are essentially expressing it as a fraction of 100 or scaling it down by a factor of 100.
- Percentages: Express numbers out of 100 (e.g., 25% is the same as saying 25 out of 100).
- Decimals: Represent parts of a whole (e.g., 0.25 represents a quarter or 25 out of 100).
The Basics of Conversion
Converting a percent to a decimal involves dividing the percentage by 100. Here’s how you do it:
- Identify the percentage: For example, 50%.
- Divide by 100: 50 ÷ 100 = 0.50.
This simple division by 100 turns the percentage into its decimal form.
Converting Percentages to Decimals: Step-by-Step

Let’s walk through the conversion process with some examples:
Example 1: 15%

- Step 1: Identify the percentage - 15%.
- Step 2: Divide by 100 - 15 ÷ 100 = 0.15.
Example 2: 7.5%

- Step 1: Identify the percentage - 7.5%.
- Step 2: Divide by 100 - 7.5 ÷ 100 = 0.075.
Example 3: 3%

- Step 1: Identify the percentage - 3%.
- Step 2: Divide by 100 - 3 ÷ 100 = 0.03.
💡 Note: When dealing with decimal percentages, remember to keep track of all the decimal places for accuracy.
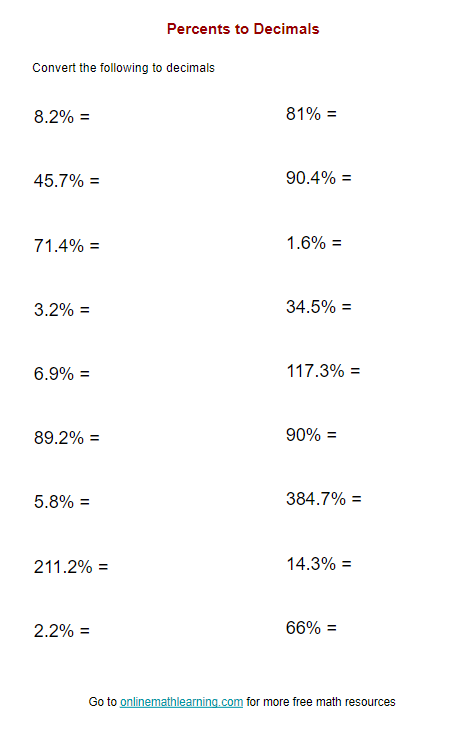
Worksheet for Practice

Now that we’ve covered the theory, here’s a worksheet to help you practice converting percents to decimals:
| Percent | Decimal Equivalent |
|---|---|
| 20% | |
| 90% | |
| 5.5% | |
| 0.5% |

Complete this worksheet to solidify your understanding.
Applications of Converting Percents to Decimals

Knowing how to convert between percentages and decimals has practical applications in various fields:
- Finance: Calculating interest rates, discounts, taxes, etc.
- Mathematics: Solving proportion problems and equations.
- Statistics: Interpreting data, especially when dealing with percentage distributions.
Handling Difficult Conversions

What if you’re confronted with trickier scenarios?
Example 1: 125%

- Step 1: Identify the percentage - 125%.
- Step 2: Divide by 100 - 125 ÷ 100 = 1.25.
Example 2: -23%

- Step 1: Identify the percentage - -23%.
- Step 2: Divide by 100 - -23 ÷ 100 = -0.23.
⚠️ Note: Don't forget about negative percentages; they become negative decimals.
Moving Forward

By now, you should have a clear understanding of how to convert percents to decimals. Remember to practice regularly to become proficient. Once you’ve mastered this skill, you’ll find that calculating percentages and dealing with financial, statistical, or simple math problems becomes significantly easier. This guide provides you with the tools to convert percentages with confidence, enhancing your problem-solving capabilities in various contexts. Keep exploring and applying these conversions in your daily life, and soon, this skill will become second nature.
Why do we divide percentages by 100 to get decimals?

+
The term “percent” means “per hundred.” Therefore, converting any percentage to a decimal involves dividing it by 100 to reflect its proportion out of 100.
How do you convert a negative percentage to a decimal?

+
Just like with positive percentages, you divide the negative percentage by 100. For example, -20% would become -0.20.
What if the percentage has decimals itself?

+
Decimal percentages are converted in the same manner, you simply keep track of the decimal places when dividing by 100. For example, 3.25% becomes 0.0325.