5 Simple Steps to Convert Fractions to Decimals

Converting fractions to decimals is a foundational arithmetic skill that can be handy in various situations, from basic math assignments to real-life applications like cooking or finance. This skill simplifies mathematical operations and makes understanding and comparing numbers easier. Here, we will explore five simple steps to convert any fraction into a decimal.
Understanding the Basics


Before diving into the conversion process, it’s beneficial to understand what a fraction represents. A fraction is essentially a part of a whole, where the numerator (top number) tells you how many parts you have, and the denominator (bottom number) indicates how many equal parts make up the whole. For example, in the fraction (\frac{3}{4}), 3 is the numerator, and 4 is the denominator, meaning you have 3 out of 4 equal parts.
Step 1: Recognize the Fraction
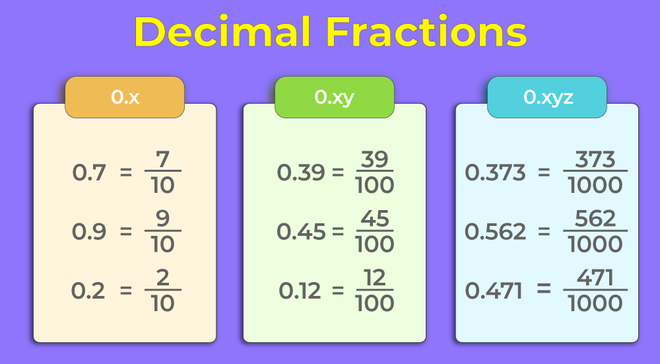
Identify the fraction you want to convert. This might seem trivial, but ensuring you have the fraction correctly noted will prevent mistakes in later steps.
Step 2: Divide the Numerator by the Denominator

This is where the actual conversion happens. Here’s how you proceed:
- Place the numerator (top number) first as the dividend.
- Then, use the denominator (bottom number) as the divisor.
- Perform the division. For instance, if you’re converting (\frac{5}{2}):
- Set up the division as (5 \div 2). The result is 2.5, which is your decimal.
Step 3: Check for Termination or Repetition

Not all fractions convert to simple decimals. Some:
- Terminate, meaning the division yields a decimal with a finite number of digits (e.g., (\frac{1}{2} = 0.5)).
- Repeat indefinitely, where the decimal repeats a pattern (e.g., (\frac{1}{3} = 0.\overline{3})).
Understanding if your decimal will terminate or repeat can help you predict the outcome of your conversion:
- Terminating decimals occur when the denominator in its prime factorization contains only 2s and 5s.
- Repeating decimals occur in all other cases.
Step 4: Simplify Your Fraction (if Possible)

Simplifying your fraction before conversion can often lead to:
- Less complex division.
- Easier understanding of whether the decimal will terminate or repeat.
To simplify:
- Find the greatest common divisor (GCD) of both the numerator and the denominator.
- Divide both numbers by this GCD. For example, (\frac{4}{8}) simplifies to (\frac{1}{2}), which we’ve already seen converts to 0.5.
Step 5: Review Your Work

Lastly, ensure your conversion is accurate by reviewing:
- Recheck your division.
- Compare your result with an online calculator or a reference table to confirm accuracy.
| Fraction | Decimal Equivalent |
|---|---|
| (\frac{1}{2}) | 0.5 |
| (\frac{1}{4}) | 0.25 |
| (\frac{3}{4}) | 0.75 |
| (\frac{1}{3}) | 0.\overline{3} |

After following these steps, you'll find that converting fractions to decimals isn't as daunting as it might seem. Whether for school, work, or everyday tasks, understanding this process can streamline mathematical operations and make numerical comparisons more straightforward.
What if my decimal conversion results in a repeating pattern?

+
Repeating decimals signify that the fraction you started with was not a terminating decimal. The repeating digits or group of digits (denoted with a bar over them) means the number does not end. For example, ( \frac{1}{3} = 0.\overline{3} ).
Can every fraction be expressed as a decimal?

+
Yes, every fraction can be expressed as a decimal, though not all will be terminating decimals. Some will be repeating decimals, indicating they represent a rational number with a non-terminating decimal expansion.
How do I convert decimals back to fractions?

+
To convert a decimal back to a fraction, look at the place value of the last digit in the decimal. Write the decimal as a fraction where the numerator is the decimal number and the denominator is a power of 10 corresponding to the place value. Simplify if possible.
Is there a quick way to check if a fraction will result in a terminating decimal?

+
Yes, if the denominator, when reduced to its prime factors, contains only the primes 2 and 5, the decimal will terminate. Otherwise, it will repeat.
Why is it important to simplify fractions before converting?

+
Simplifying fractions first reduces the complexity of the division you’ll need to perform to get the decimal, potentially making the calculation easier and less prone to error.