5 Ways to Master the Converse of the Pythagorean Theorem
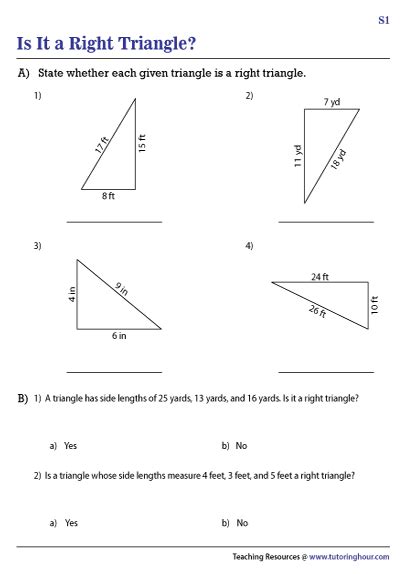
Unlocking the Secrets of the Converse of the Pythagorean Theorem
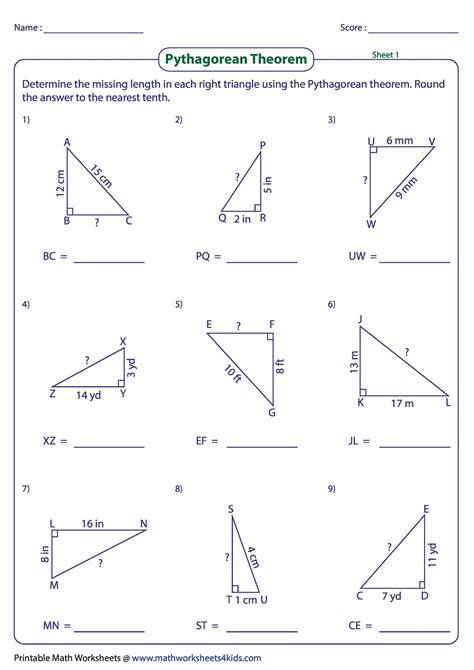
The Pythagorean Theorem is a fundamental concept in geometry, used to calculate the length of the hypotenuse of a right-angled triangle. However, the converse of the Pythagorean Theorem is just as important, as it allows us to determine whether a triangle is right-angled or not. In this article, we will explore five ways to master the converse of the Pythagorean Theorem, including understanding the concept, applying it to different types of triangles, and using real-world examples.
Understanding the Converse of the Pythagorean Theorem

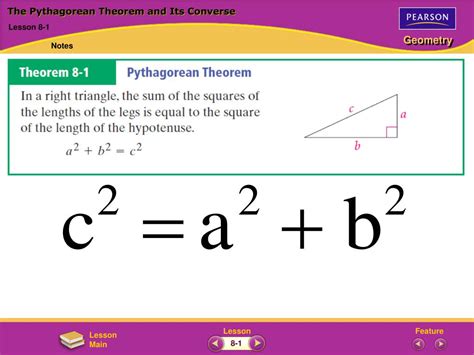
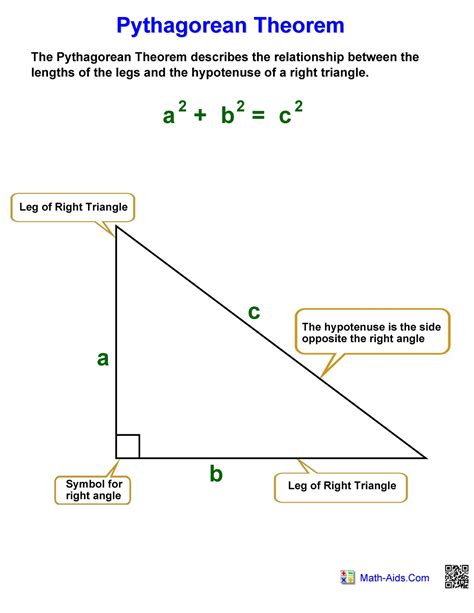
The converse of the Pythagorean Theorem states that if the square of the length of the longest side of a triangle is equal to the sum of the squares of the lengths of the other two sides, then the triangle is right-angled. This can be expressed mathematically as:
a^2 + b^2 = c^2
where a and b are the lengths of the two shorter sides, and c is the length of the longest side (the hypotenuse).
Key Points to Remember
- The converse of the Pythagorean Theorem only works for triangles with three sides of different lengths.
- The longest side of the triangle must be the hypotenuse.
- The theorem can be used to determine whether a triangle is right-angled or not.
Method 1: Using the Converse to Check for Right-Angled Triangles
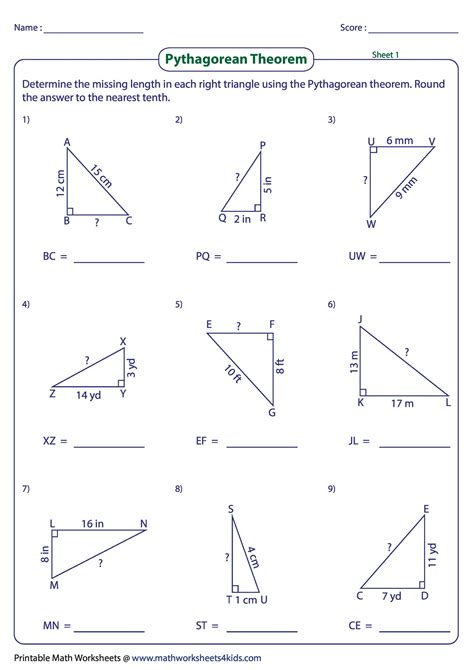
One way to master the converse of the Pythagorean Theorem is to use it to check whether a triangle is right-angled or not. To do this, simply plug the lengths of the three sides into the equation above and see if it holds true. If the equation is true, then the triangle is right-angled.
📝 Note: Make sure to use the correct units when measuring the lengths of the sides. This will ensure that your calculations are accurate.
Method 2: Applying the Converse to Real-World Scenarios

The converse of the Pythagorean Theorem has many real-world applications, such as building design, physics, and engineering. By applying the theorem to real-world scenarios, you can gain a deeper understanding of its importance and relevance.
For example, imagine you are a builder designing a new house. You want to make sure that the roof is right-angled, so you use the converse of the Pythagorean Theorem to check the measurements.
Real-World Example
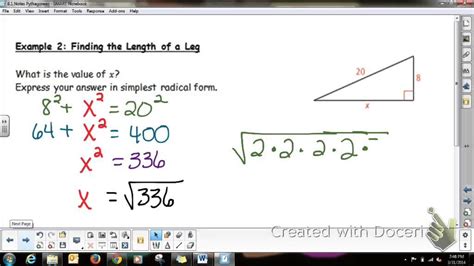
Suppose you are building a roof with two sides of length 3 meters and 4 meters, and you want to know whether the angle between them is 90 degrees. Using the converse of the Pythagorean Theorem, you can calculate the length of the hypotenuse (the longest side) as follows:
3^2 + 4^2 = c^2 9 + 16 = c^2 25 = c^2
Taking the square root of both sides, you get:
c = √25 c = 5 meters
Since the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides, the angle between them is 90 degrees, and the triangle is right-angled.
Method 3: Using the Converse to Solve Triangles
The converse of the Pythagorean Theorem can also be used to solve triangles, especially those with three sides of different lengths. By using the theorem, you can determine the length of the longest side (the hypotenuse) and then use the Pythagorean Theorem to find the other two sides.
🤔 Note: Make sure to use the correct formula when solving triangles. The converse of the Pythagorean Theorem is only applicable to right-angled triangles.
Method 4: Visualizing the Converse with Diagrams
Visualizing the converse of the Pythagorean Theorem with diagrams can help you understand the concept better. By drawing a diagram of a right-angled triangle, you can see how the theorem works and how it can be applied to different types of triangles.
Example Diagram
Here is an example diagram of a right-angled triangle with two sides of length 3 meters and 4 meters:
/|
/ |
/__|
/ \
/______\
/ \
/___________\
In this diagram, the longest side (the hypotenuse) is labeled as c, and the other two sides are labeled as a and b.
Method 5: Practicing with Different Types of Triangles
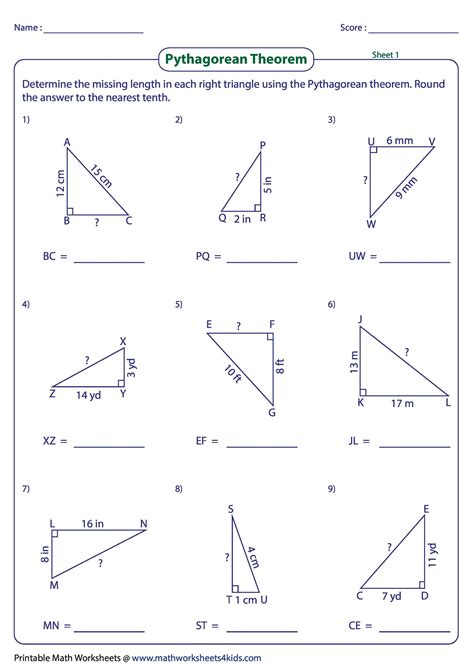
Finally, mastering the converse of the Pythagorean Theorem requires practice with different types of triangles. By practicing with different types of triangles, you can become more familiar with the theorem and its applications.
Types of Triangles to Practice With
Here are some types of triangles to practice with:
- Right-angled triangles with two sides of equal length (e.g. 3-4-5 triangle)
- Right-angled triangles with two sides of different lengths (e.g. 5-12-13 triangle)
- Oblique triangles with three sides of different lengths (e.g. 6-8-10 triangle)
By practicing with these types of triangles, you can become more confident in your ability to apply the converse of the Pythagorean Theorem.
In summary, mastering the converse of the Pythagorean Theorem requires a combination of understanding the concept, applying it to different types of triangles, and practicing with real-world examples.
What is the converse of the Pythagorean Theorem?

+
The converse of the Pythagorean Theorem states that if the square of the length of the longest side of a triangle is equal to the sum of the squares of the lengths of the other two sides, then the triangle is right-angled.
How do I apply the converse of the Pythagorean Theorem to real-world scenarios?

+
You can apply the converse of the Pythagorean Theorem to real-world scenarios such as building design, physics, and engineering. By using the theorem, you can determine whether a triangle is right-angled or not.
What types of triangles should I practice with to master the converse of the Pythagorean Theorem?

+
You should practice with different types of triangles, including right-angled triangles with two sides of equal length, right-angled triangles with two sides of different lengths, and oblique triangles with three sides of different lengths.
Related Terms:
- Pythagorean Theorem Worksheet PDF
- kuta pythagorean theorem word problems
- pythagorean converse worksheet pdf
- proof of converse bpt theorem
- converse of pythagoras worksheets pdf
- converse of pythagoras worksheets



