5 Math Worksheets to Master Pythagorean Theorem Converse

Ever since the ancient Greek mathematician Pythagoras formulated his famous theorem, it has been a cornerstone in the study of geometry. His theorem not only helped in understanding the relationship between the sides of a right-angled triangle but also has numerous applications in various fields like architecture, engineering, and computer science. Understanding and mastering the Pythagorean Theorem Converse can be a challenging yet rewarding endeavor. Here, we present five meticulously crafted math worksheets that aim to deepen your understanding of this fundamental geometric principle.
Theoretical Foundation of the Pythagorean Theorem Converse
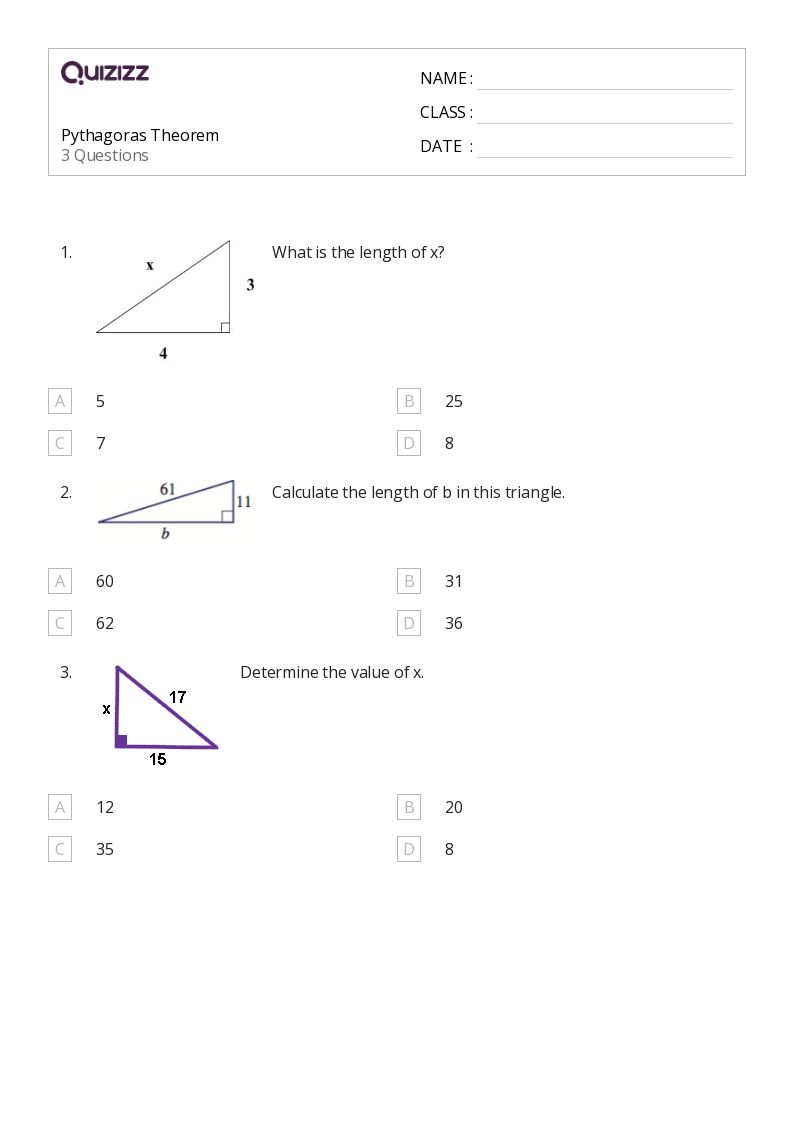
The Pythagorean Theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. Mathematically, this is expressed as:
- c2 = a2 + b2
The Converse of the Pythagorean Theorem asserts that if the square of the length of the longest side of a triangle equals the sum of the squares of the lengths of the other two sides, then the triangle is a right triangle. This can be particularly useful when verifying if a triangle has a right angle. Understanding this converse can:
- Identify right triangles
- Check if a triangle has a right angle
- Solve problems where right triangles might not be immediately apparent
Worksheet 1: Basics of the Pythagorean Theorem Converse


This worksheet focuses on:
- Calculating if a triangle is a right triangle using the converse
- Understanding the concept through visual and numerical examples
- Solving simple problems to reinforce the concept
🔍 Note: Students should ensure they know how to square numbers and understand the relationship between sides in a right triangle.
Worksheet 2: Applications in Real-World Scenarios


Here, we apply the theorem to:
- Architecture and construction
- Surveying for land measurement
- Calculating distances in navigational routes
This worksheet not only reinforces the theorem but also helps students connect math with real-world problems.
Worksheet 3: Proving the Converse


Understanding the proof of the Pythagorean Theorem Converse can:
- Demonstrate the theorem's validity
- Help with logical reasoning and geometric proofs
- Enhance problem-solving skills through deductive reasoning
Worksheet 4: Complex Scenarios and Problem Solving


This worksheet delves into:
- Multiple choice questions to test understanding
- Scenarios with multiple triangles or shapes
- Word problems requiring logical reasoning and setup
It challenges students to apply the theorem in more complex situations, enhancing their ability to manipulate geometric relationships.
Worksheet 5: Interactive Learning Through Visuals


Interactive visuals:
- Help visualize the relationship between the sides
- Engage students with animations or diagrams
- Allow for hands-on learning through activities or simulations
🌟 Note: Interactive elements make learning more engaging and can provide immediate feedback on understanding.
Summary

These five worksheets are designed to take students from the basic understanding of the Pythagorean Theorem Converse to applying it in complex scenarios, proving its validity, and interacting with visuals. By mastering the converse, students not only gain a deeper appreciation for geometric principles but also equip themselves with tools useful in various fields of study and practical life.
Why is mastering the Pythagorean Theorem Converse important?

+
Understanding the converse helps in verifying if a triangle has a right angle, which is crucial in fields like construction, architecture, and surveying.
How can these worksheets help in learning?

+
The worksheets provide structured learning from basics to complex applications, incorporating visual learning, real-world problems, and interactive elements for comprehensive understanding.
What other skills can I develop through these worksheets?

+
You’ll develop skills in problem-solving, logical reasoning, geometric proofs, and real-world application of mathematical concepts.