5 Key Insights from the Constant Velocity Worksheet

The concept of constant velocity plays a pivotal role in understanding motion in physics. Whether you're a student grappling with high school physics or an enthusiast exploring the fundamentals of mechanics, the constant velocity worksheet provides a foundational understanding of how objects move. Here are five key insights derived from working through such a worksheet:
1. Understanding Uniform Motion

Uniform motion refers to an object moving at a constant speed in a straight line. This means the object’s velocity neither increases nor decreases over time. The constant velocity worksheet typically explores:
- The definition of velocity as speed in a given direction
- How to calculate velocity using the formula ( v = \frac{d}{t} ) (where ( v ) is velocity, ( d ) is displacement, and ( t ) is time)
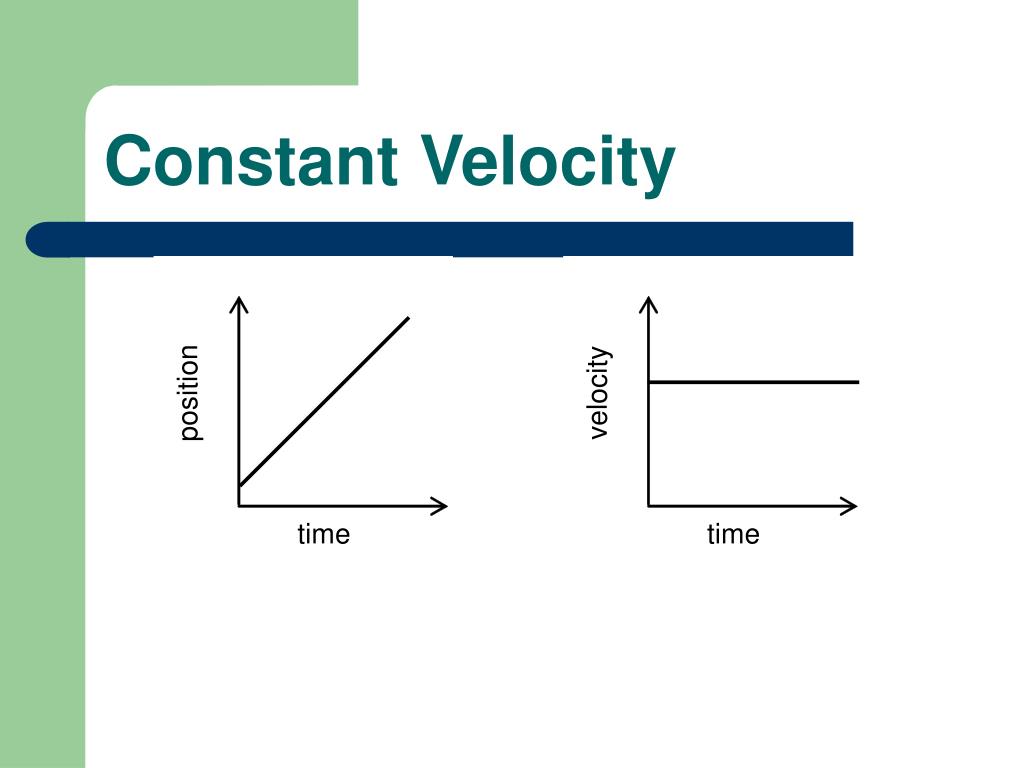
- The graphical representation of uniform motion on a distance-time graph where the slope represents velocity
🔍 Note: A horizontal line on a velocity-time graph indicates zero acceleration, confirming uniform motion.
2. Velocity and Displacement

Displacement is a vector quantity, meaning it has both magnitude and direction. Here’s how to navigate this:
- Understand the vector nature of velocity: displacement gives direction to the movement.
- Calculate average velocity by dividing total displacement by total time.
- Interpret how changes in direction affect total displacement and hence average velocity.
3. Time and Speed

Time is an essential factor when discussing velocity:
- Learn how to convert between different time units to accurately solve velocity problems.
- Distinguish between instantaneous speed and average speed.
- Analyze how speed remains constant but direction can change, leading to varying velocities.
| Time | Distance (m) | Velocity (m/s) |
|---|---|---|
| 0s | 0 | 0 |
| 2s | 8 | 4 |
| 4s | 16 | 4 |
| 6s | 24 | 4 |
| 8s | 32 | 4 |

4. Graphical Analysis

The constant velocity worksheet often involves graphing:
- Recognize that the slope of the distance-time graph at any point equals the object’s speed.
- Use distance-time and velocity-time graphs to determine if motion is uniform.
- Learn to interpret displacement and velocity changes from the graphs.
5. Practical Applications

Constant velocity isn’t just an academic exercise; it has real-world implications:
- Analyzing traffic flow in urban planning
- Optimizing vehicle performance in automotive engineering
- Understanding human and animal motion patterns in biomechanics
- Navigating celestial bodies in space travel
🔎 Note: The applications of uniform motion extend beyond these, influencing design, efficiency, and safety in various technologies.
In summary, working through a constant velocity worksheet teaches us more than just equations. It reveals how objects behave when subjected to forces or lack thereof, offering a deeper insight into the physical world. From the fundamental definitions to the practical applications, mastering the concept of constant velocity is essential for anyone aspiring to understand or work with motion. The journey through this worksheet not only hones mathematical skills but also fosters a nuanced appreciation of how physics explains and enhances our interaction with the universe.
What is the difference between average and instantaneous velocity?

+
Average velocity is calculated by dividing total displacement by total time traveled, providing an overall view of the motion. Instantaneous velocity, on the other hand, refers to the velocity at a specific moment in time. It represents the slope of the tangent line on a distance-time graph at that instant.
Can an object have constant velocity if it changes direction?

+
No, if an object changes direction, its velocity cannot be constant because velocity is a vector quantity with both magnitude and direction. A change in direction means a change in velocity.
How can you tell if an object is moving at a constant velocity from a graph?

+
On a distance-time graph, a straight line with a constant slope indicates constant velocity. On a velocity-time graph, a horizontal line represents constant velocity because it indicates that the velocity is not changing over time.
Why is uniform motion important in practical applications?
+
Uniform motion simplifies the analysis of complex systems, making it easier to predict and control the behavior of objects. It’s essential in optimizing vehicle performance, traffic flow, and in designing efficient transportation and navigation systems.
What are some common misconceptions about constant velocity?

+
One common misconception is that speed and velocity are the same; however, velocity includes direction. Another is thinking that acceleration can be present with constant velocity, which is not true in a straight line; acceleration implies a change in velocity.