5 Tips for Mastering Constant Velocity Worksheets
Mastering constant velocity worksheets is essential for students delving into physics, especially in understanding motion, speed, and distance. Constant velocity implies an object moves with a uniform speed in a straight line, without any acceleration. For many students, this concept can be the starting point for exploring more complex motion dynamics. Here are some detailed tips to help you become proficient in solving these types of problems:
1. Understand the Concept of Constant Velocity

Before you dive into solving problems, ensure you have a solid grasp of what constant velocity means. Remember, the speed and direction of motion do not change. Here’s what you should know:
- Speed: The rate at which an object covers distance.
- Direction: Always linear and constant in velocity problems.
- Formula: Velocity = Distance / Time
- Key Equation: v = Δx / Δt
💡 Note: Constant velocity doesn’t mean constant speed; it means constant speed and direction.

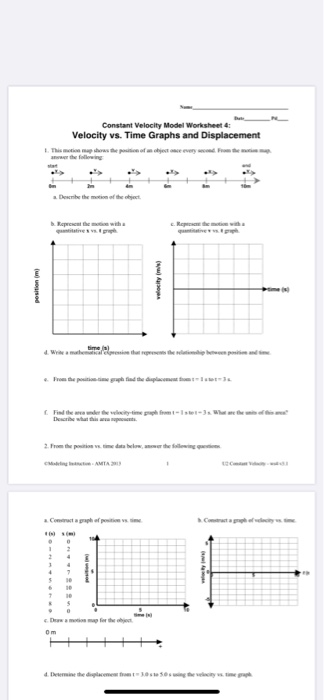
2. Master the Distance-Time Graph

A distance-time graph is a visual representation of an object’s motion at constant velocity:
- The slope of the graph represents the object’s velocity.
- Straight line implies constant velocity.
- Vertical axis measures distance, and the horizontal axis is time.
| Graph Feature | What it Signifies |
|---|---|
| Slope | Velocity (Constant) |
| Horizontal Line | Object at Rest (Velocity = 0) |

🔎 Note: A steeper slope indicates a higher velocity, and a straight horizontal line indicates no motion.
3. Solve Using the Velocity-Time Equation

The velocity-time equation is a simple tool for solving constant velocity problems:
- v = (d2 - d1) / (t2 - t1)
- Where v is velocity, d is distance, and t is time.
Follow these steps to solve using this equation:
- Identify initial and final distances (d1, d2).
- Identify initial and final times (t1, t2).
- Calculate the velocity.
Example:
- Car moves from point A to point B, which is 100 meters apart in 5 seconds.
- v = (100m - 0m) / (5s - 0s) = 20 m/s
4. Practice with Word Problems

Word problems help in understanding how to apply theoretical concepts in real-world scenarios. Here are some tips:
- Identify the given variables (distance, time, speed, direction).
- Determine if the problem involves constant velocity or acceleration.
- Use the provided information to solve for the unknown variable.
Example Problem:
- A runner runs at 5 m/s for 30 seconds. How far does he run?
- v = 5 m/s, t = 30 s
- d = v * t = 5 * 30 = 150 meters
📝 Note: Practice regularly to understand the nuances of word problems and their application.
5. Create Your Own Problems

Creating your own constant velocity problems is an excellent way to test your understanding:
- Choose everyday scenarios or fictional ones to make it interesting.
- Develop questions based on real-life travel, sports, or mechanical motion.
- Exchange problems with classmates for peer review and learning.
Here’s how you can craft your own problem:
- Scenario: A bike travels at a constant speed of 12 mph.
- Question: How long will it take to travel 6 miles?
- Solution: t = d / v = 6 miles / 12 mph = 0.5 hours
By following these tips, you’ll be well-equipped to handle constant velocity problems confidently. Remember, the key to mastering any subject in physics is understanding the concepts and applying them consistently. Keep practicing, and over time, you'll notice that these problems become second nature. Whether it's through graphical analysis, equation-based solutions, or word problem-solving, each method provides a unique perspective on understanding constant velocity.
How do I know if an object is moving at constant velocity?

+
An object has constant velocity if its speed and direction of motion do not change. This can be observed in a distance-time graph where the slope of the line is constant or calculated using the equation v = Δx / Δt, where both Δx (change in distance) and Δt (change in time) result in a consistent velocity value.
Can an object have constant velocity but changing speed?
+
No, velocity encompasses both speed and direction. If either changes, the velocity is no longer constant.
Why is it important to practice with word problems?

+
Word problems simulate real-world scenarios where you need to extract information to solve for unknowns. They help develop critical thinking, application of formulas, and interpretation of results, which are vital for understanding physics.