5 Essential Worksheets for Mastering Proportionality
Understanding the concept of proportionality is fundamental for students at various levels of education, as it plays a crucial role in subjects like Mathematics, Physics, and even in everyday scenarios such as cooking or financial planning. Proportionality involves understanding how quantities relate to each other when they are directly or inversely proportional. To aid in mastering this concept, educators and students can benefit from well-structured worksheets. Here, we'll explore five essential worksheets designed to enhance understanding and practice of proportionality.
1. Understanding Direct Proportionality


Direct proportionality exists when an increase in one quantity results in a proportional increase in another. This worksheet:
- Introduces the concept of direct proportionality with real-life examples.
- Includes problems where students calculate unknown quantities using given ratios.
- Offers graphs to visually represent the relationship.
📝 Note: Always make sure students understand that in direct proportionality, if one value doubles, the other value doubles as well.
2. Inverse Proportionality Worksheet


Inverse proportionality occurs when an increase in one quantity leads to a decrease in the other, maintaining a constant product. This worksheet:
- Explains how inverse proportionality works through practical scenarios.
- Provides exercises where students solve for variables in an inverse proportion relationship.
- Uses visual representations to show how quantities change inversely.
Using tables can be effective in understanding inverse proportionality:
| Quantity A | Quantity B | Product (A × B) |
|---|---|---|
| 5 | 4 | 20 |
| 10 | 2 | 20 |

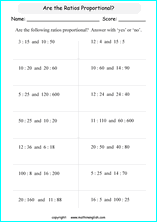
3. Comparing Proportions

Understanding how to compare proportions is vital for higher-order math problems. This worksheet:
- Asks students to compare and contrast different proportions.
- Involves setting up and solving proportion equations.
- Introduces the cross-multiplication method to solve proportions.
4. Practical Applications of Proportionality


This worksheet focuses on real-world applications:
- Scenarios like recipe scaling, map reading, and financial calculations.
- Problems involving rate of work, distance, time, and speed.
- Incorporates critical thinking to apply proportionality in new contexts.
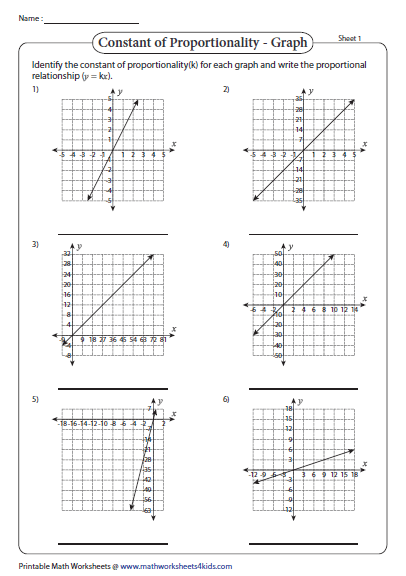
5. Graphing Proportional Relationships

Graphical representation is key to understanding proportionality:
- Worksheet guides students in plotting direct and inverse proportion graphs.
- Includes exercises on interpreting graphs and identifying slopes or hyperbolas.
- Encourages the use of technology or grid paper for accurate plotting.
By engaging with these worksheets, students gain a thorough understanding of proportionality, which is not only useful for mathematical proficiency but also for problem-solving in various professional fields and daily life. As students progress through these exercises, they will: - Recognize different types of proportionality. - Solve practical problems involving direct and inverse proportions. - Compare, graph, and interpret proportional relationships. These skills foster a deeper appreciation of mathematical concepts and their applications, enhancing overall problem-solving abilities and logical reasoning.
What is the difference between direct and inverse proportionality?

+
In direct proportionality, an increase in one quantity leads to a proportional increase in another, while inverse proportionality means one quantity increases as the other decreases, maintaining a constant product.
How can I use proportionality in everyday life?

+
Proportionality is useful in scenarios like scaling recipes, understanding financial investments (e.g., calculating interest rates), or determining time and distance relationships in travel.
Why is graphing important in understanding proportionality?

+
Graphing helps visualize how quantities change relative to each other, making it easier to identify whether the relationship is direct, inverse, or another type of function.