Constant of Proportionality Worksheet: Graphing Made Easy

Understanding the constant of proportionality is crucial in mathematics, particularly when dealing with proportional relationships. This blog post will guide you through the process of graphing proportional relationships, helping you to identify the constant of proportionality with ease. Whether you're a student, teacher, or just someone interested in math, this comprehensive worksheet will provide you with the tools to enhance your understanding.
What is Proportional Relationship?
A proportional relationship exists when two quantities, say (x) and (y), vary together at a constant rate. This means that if you double one quantity, the other will also double, maintaining a fixed ratio. Mathematically, this relationship can be described with the formula:
[ y = kx ]where:
- y is the dependent variable
- x is the independent variable
- k is the constant of proportionality
Identifying Proportional Relationships

To determine if a relationship is proportional, you can look for:
- A graph that passes through the origin (0,0).
- A table or set of values where the ratio of (y) to (x) remains constant.
- An equation where (y) is directly proportional to (x).
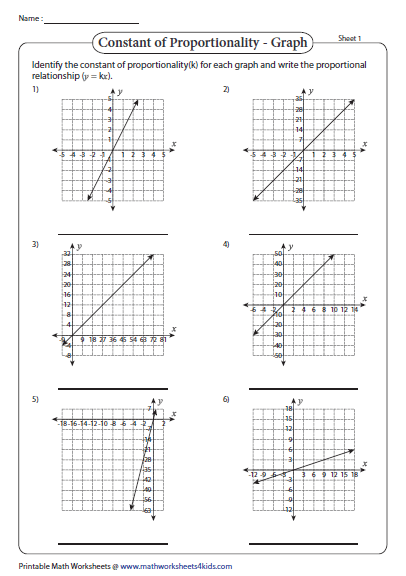
Graphing Proportional Relationships

Graphing helps visualize the relationship and determine the constant of proportionality. Here’s how you can do it:
- Plot Points: If you have a set of values, plot these on a graph where x is on the horizontal axis and y on the vertical axis.
- Draw the Line: Connect the points. For a proportional relationship, this line should pass through the origin.
- Find the Slope: The slope of this line is the constant of proportionality, (k).

Worksheet for Practice

Let’s engage with some practical exercises:
Exercise 1: Identifying Proportions

Given the following sets of data, determine if they represent a proportional relationship:
| Set A | Set B | Set C | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|

Exercise 2: Graphing and Identifying k

Graph the following data and determine the constant of proportionality:
- y = 1, when x = 2
- y = 3, when x = 6
- y = 5, when x = 10
Notes:
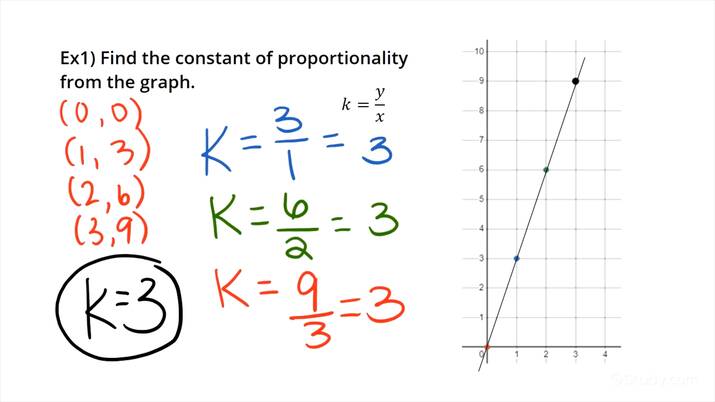
📌 Note: Remember, for a proportional relationship, the graph will be a straight line passing through the origin.
📊 Note: The slope of the line (which you can calculate from any two points) gives you the constant of proportionality.
✏️ Note: Use a straightedge or ruler when drawing lines for accuracy.
The process of graphing and understanding proportional relationships can make complex mathematical concepts more tangible and manageable. With the provided exercises, you have the opportunity to practice identifying and graphing these relationships, thereby deepening your comprehension of the constant of proportionality. The examples and instructions laid out here should provide you with a clear pathway to understanding these fundamental mathematical principles, ensuring that you are equipped to tackle related problems with confidence.
What does the constant of proportionality represent in real-life scenarios?

+
In real-life, the constant of proportionality can represent rates such as speed, unit price, or any other consistent relationship between two quantities. For instance, if you’re driving at a constant speed, the distance traveled (y) is directly proportional to time (x), and the speed is the constant of proportionality.
How can I tell if a relationship is not proportional just by looking at the graph?

+
A relationship is not proportional if the line on the graph does not pass through the origin, or if it’s not a straight line at all. Any curvature or an intercept away from the origin signifies a non-proportional relationship.
Can the constant of proportionality be negative?

+
Yes, the constant of proportionality can be negative. This indicates an inverse proportionality where as one quantity increases, the other decreases. For example, in physics, if force (F) is applied against the motion of an object, the velocity (v) might decrease in proportion to the force, with the proportionality constant being negative.
What are some common mistakes to avoid when identifying the constant of proportionality?

+
Common mistakes include:
- Not verifying if the graph passes through the origin.
- Calculating the slope incorrectly by mixing up the coordinates.
- Assuming a relationship is proportional without checking that (y/x) is constant across all data points.
- Forgetting that the constant can also be fractional or negative.
How can I apply proportional relationships in everyday tasks?

+
Proportional relationships are applicable in many daily activities:
- Cooking or baking, where recipes need to be scaled up or down.
- Mixing solutions in chemistry, where the concentration must remain constant.
- Calculating distance or time based on a constant speed.
- Financial calculations like cost per unit or compound interest calculations.