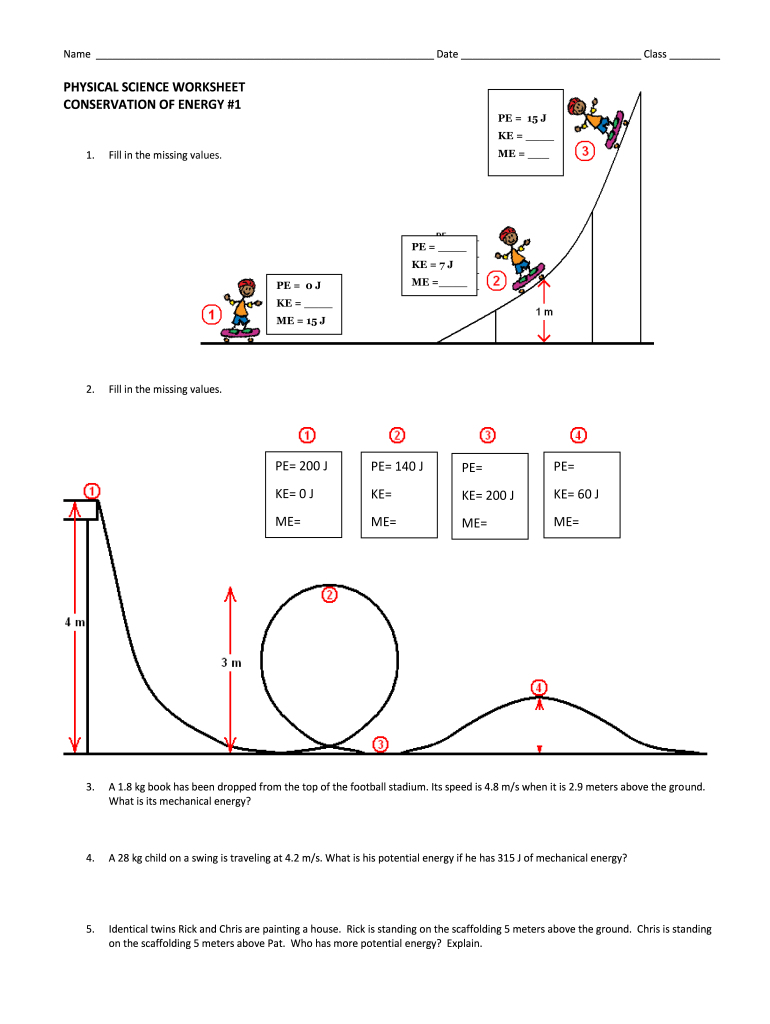
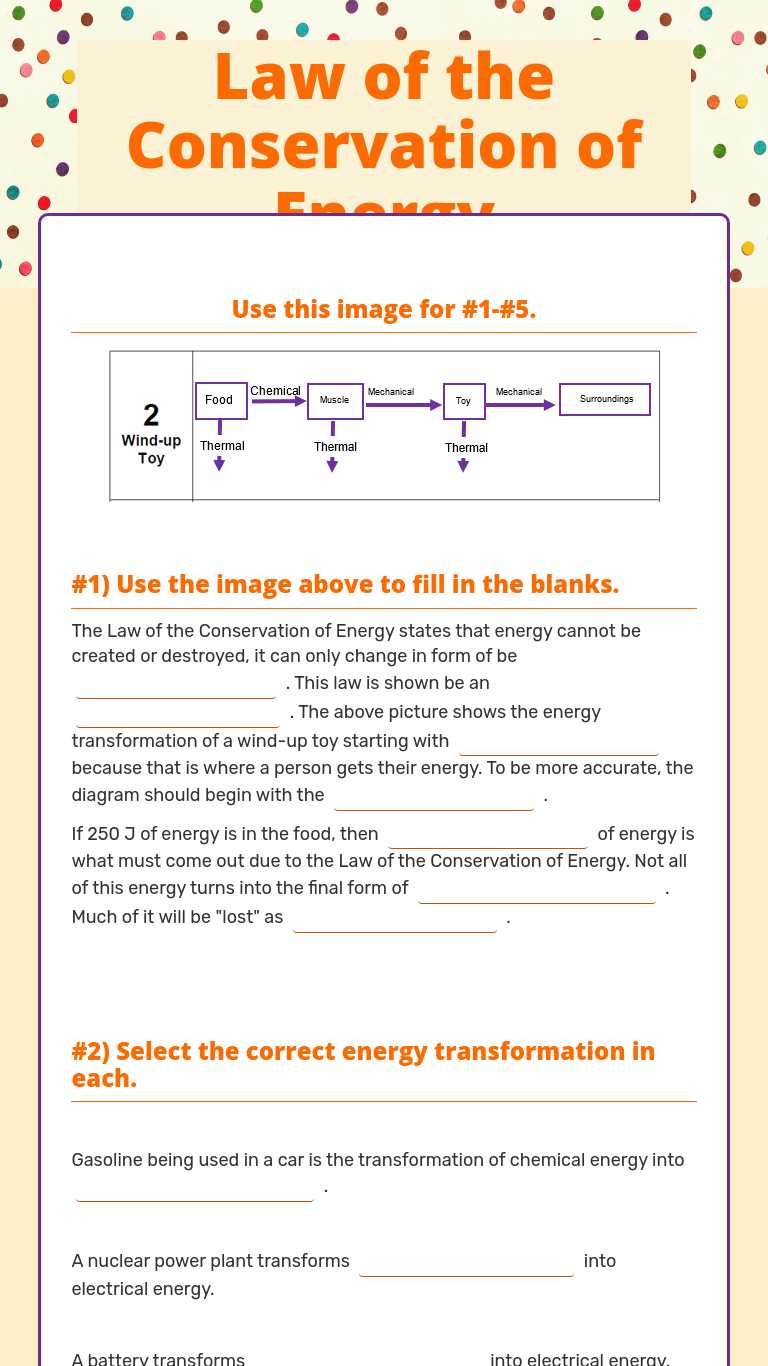
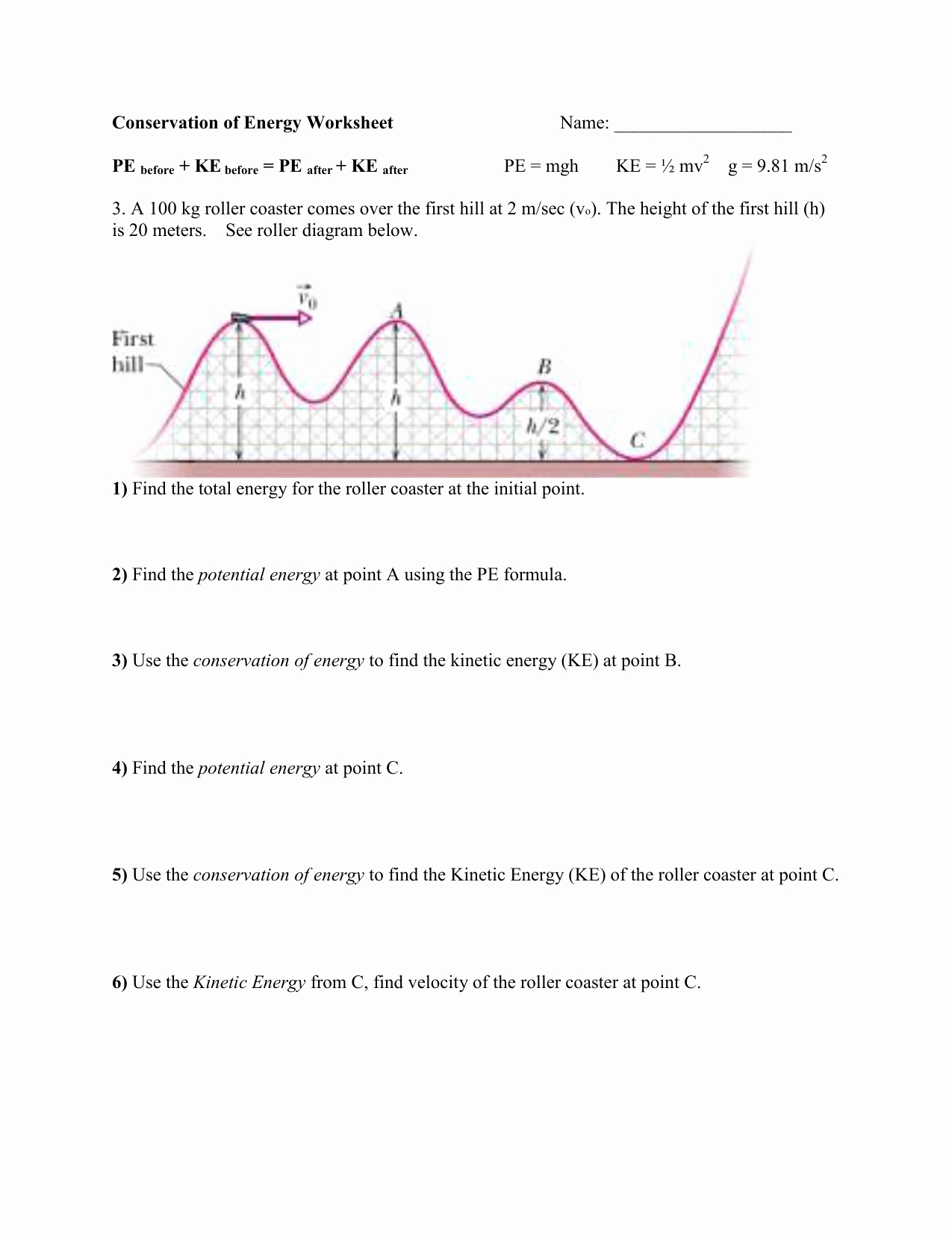
Conservation of Energy Worksheet Answers: Unlock Physics Mastery

In the quest to understand the intricate dance of energy transformation and conservation, students and enthusiasts of physics often encounter complex principles that underpin much of the physical world. The Conservation of Energy is not just a theorem; it's a fundamental law that serves as the backbone for numerous natural phenomena and technological advancements. This worksheet aims to not only solidify your grasp on this law but also to provide you with answers to common problems, ensuring you unlock your physics mastery.
Understanding the Principle of Conservation of Energy

At the core of physics lies the principle of Conservation of Energy, which asserts that energy can neither be created nor destroyed. Instead, energy can only be transformed from one form to another or transferred from one object to another. Here’s a deeper look into its applications:
- Mechanical Energy Conservation: This is often illustrated in scenarios involving potential and kinetic energy. For instance, the total mechanical energy of a body in a conservative field, like gravity, remains constant.
- Work-Energy Theorem: This theorem describes how work done on an object changes its kinetic energy. If non-conservative forces like friction are involved, these forces often dissipate energy as heat, altering the total mechanical energy.
Analyzing Real-Life Examples

Let’s delve into practical examples where energy conservation can be observed and analyzed:
- A Pendulum’s Swing: When a pendulum swings, the energy is constantly transforming between kinetic and potential energy but the total energy remains conserved.
- A Roller Coaster Ride: Here, energy changes from potential energy at the top of a hill to kinetic energy as it descends. Despite friction, energy conservation principles help in predicting the speed at various points of the ride.
| Scenario | Energy at Start | Energy at Middle | Energy at End |
|---|---|---|---|
| A Ball Dropped | Potential Energy | ½ Potential Energy, ½ Kinetic Energy | Kinetic Energy |
| A Bullet Fired Horizontally | Kinetic Energy | Kinetic Energy | Some Kinetic Energy, Some Lost as Heat |

🔔 Note: Energy transformations are governed by the laws of physics, but in real-world scenarios, energy conservation might not appear absolute due to various losses like friction or air resistance.
Worksheet Problems and Answers

Here are some common questions you might find on a conservation of energy worksheet, along with their step-by-step solutions:
Problem 1
A stone with mass m falls from a height h. Assuming no air resistance, calculate its speed just before it hits the ground.
Solution:
Using the principle of conservation of energy:
- Initial PE = mgh
- At the ground, all potential energy is converted to kinetic energy: 1⁄2 * m * v^2 = mgh
- Solving for v gives v = √(2gh)
Problem 2

An object starts from rest at a height h on a frictionless ramp. What is its speed at the bottom?
Solution:
Here, again, the conservation of energy principle applies:
- Initial PE = mgh
- At the bottom, this PE has turned into KE: 1⁄2 * m * v^2 = mgh
- Thus, v = √(2gh)
Energy conservation is a theme that threads through every aspect of physics. Whether we're looking at the orbits of planets or the energy efficiency of household appliances, understanding this principle enables us to comprehend and predict the behavior of systems. Remember, energy conservation isn't just about maintaining an equation's balance; it's about seeing the world through the lens of continuity and transformation.
This exploration has not only equipped you with solutions to common worksheet problems but also enhanced your intuitive grasp of energy transformation and conservation. The principles discussed here are foundational for advancing in physics, offering insights into everything from simple mechanical systems to complex ecological balances.
Why is energy conservation important in physics?
+
Energy conservation is a cornerstone of physics because it allows us to predict and understand how systems evolve over time. It’s crucial for solving problems in mechanics, thermodynamics, electromagnetism, and even quantum physics.
Can energy be completely conserved in real-world scenarios?

+
In theoretical physics, yes, energy is conserved. However, in real-world scenarios, energy losses occur due to factors like friction, air resistance, and other non-conservative forces, which transform kinetic and potential energy into less usable forms like heat.
How can understanding energy conservation benefit everyday life?
+
From designing energy-efficient homes and vehicles to understanding the physics of everyday activities like sports or cooking, knowing how energy is conserved helps in optimizing our use of resources and understanding the impact of our actions on the environment.