Mastering Congruent Triangles: Geometry Worksheet Guide

Understanding congruent triangles is a fundamental concept in geometry that often forms the basis for more complex geometric proofs and calculations. Whether you're a student looking to conquer your geometry homework or an enthusiast aiming to brush up on your mathematical skills, mastering congruent triangles can significantly enhance your problem-solving capabilities. Here's a detailed guide to navigating through geometry worksheets involving congruent triangles.
Understanding Congruent Triangles

To start with, let’s define congruent triangles. Two triangles are said to be congruent if their corresponding sides and angles are equal in measure. This equality enables us to establish that the triangles are essentially identical in shape and size. Here are the methods to prove triangle congruence:
- Side-Side-Side (SSS): If three sides of one triangle are equal to three sides of another triangle, then the triangles are congruent.
- Side-Angle-Side (SAS): If two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, then the triangles are congruent.
- Angle-Side-Angle (ASA): If two angles and the included side of one triangle are equal to two angles and the included side of another triangle, then the triangles are congruent.
- Angle-Angle-Side (AAS): Similar to ASA but here the third angle can be deduced since the sum of angles in a triangle is always 180 degrees.
- Right Angle-Hypotenuse-Side (RHS): For right-angled triangles, if the hypotenuse and one leg are equal, then the triangles are congruent.
Approaching Geometry Worksheets

When faced with a geometry worksheet on congruent triangles, here’s a structured approach to tackle it:
1. Identify Given Information
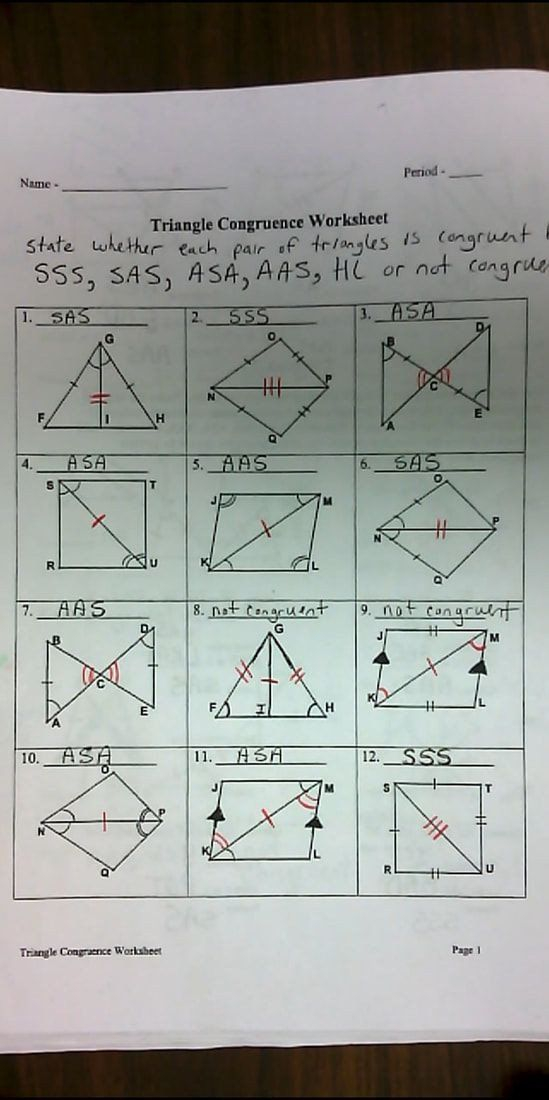
Begin by noting all given information about the triangles. This includes sides, angles, and any conditions or constraints provided:
| Information Given | Action |
|---|---|
| Side Lengths | Compare for SSS or SAS |
| Angle Measures | Use ASA, AAS, or RHS |
| Angles not directly given | Calculate them if possible |

2. Use Congruence Rules

Next, apply the congruence rules to see if the triangles match:
- Check if both triangles can be matched by applying the same rule, such as SAS or ASA.
- If one rule doesn't work, try the others. Remember, not all rules need to be applied for each set of triangles.
⚠️ Note: If a worksheet asks to prove congruence without providing all the necessary sides or angles, look for alternate methods like using parallel lines or angles formed by intersecting lines.
3. Sketch and Visualize

Often, visual aids can clarify complex problems:
- Draw the triangles according to the given information.
- Use different colors or patterns to highlight congruent parts.
4. Solve for Unknowns
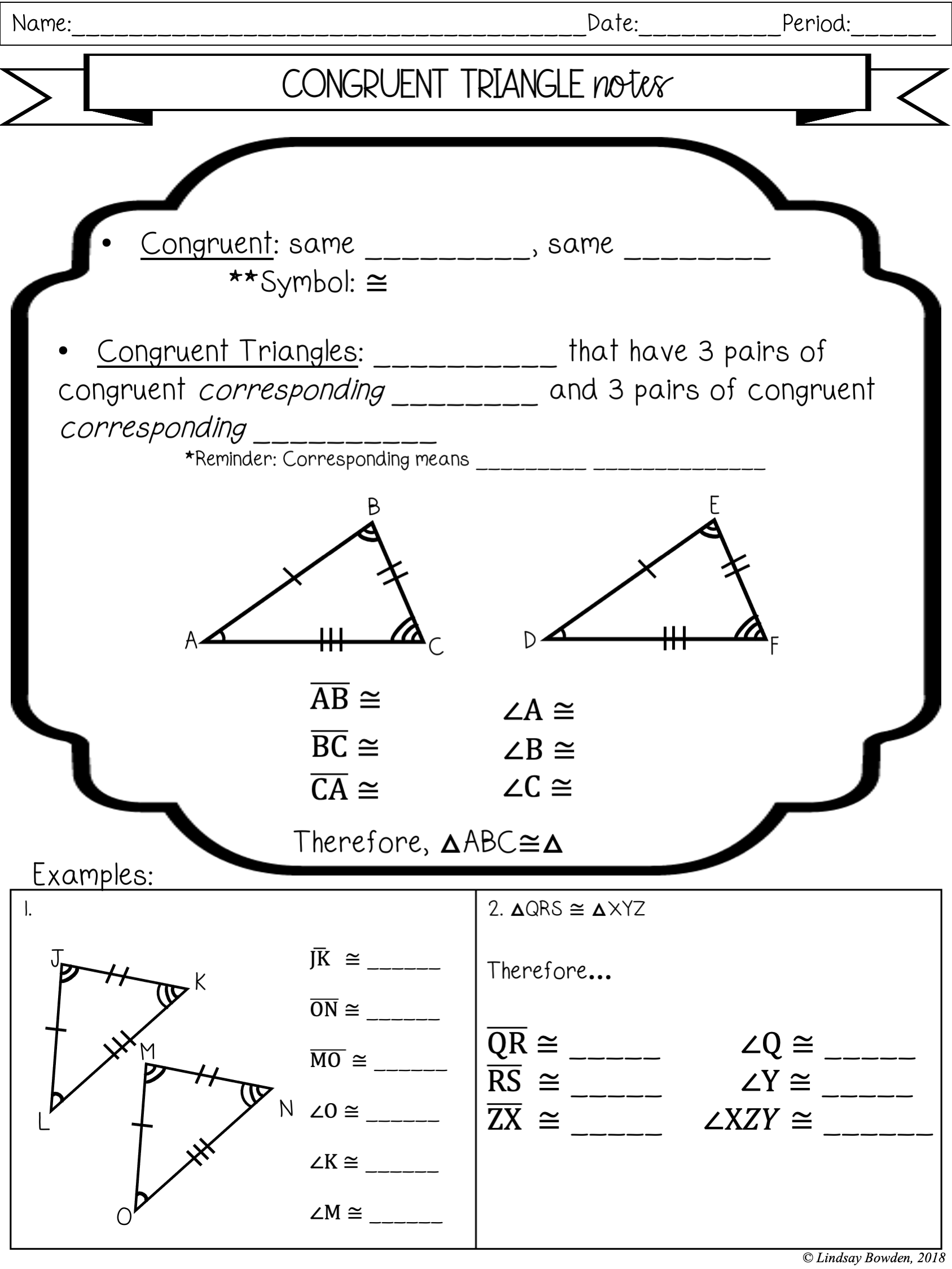
Sometimes worksheets will require you to solve for unknown sides or angles:
- Use trigonometric relationships like sine, cosine, and tangent if appropriate.
- Apply Pythagorean theorem for right-angled triangles.
5. Proofs and Constructions
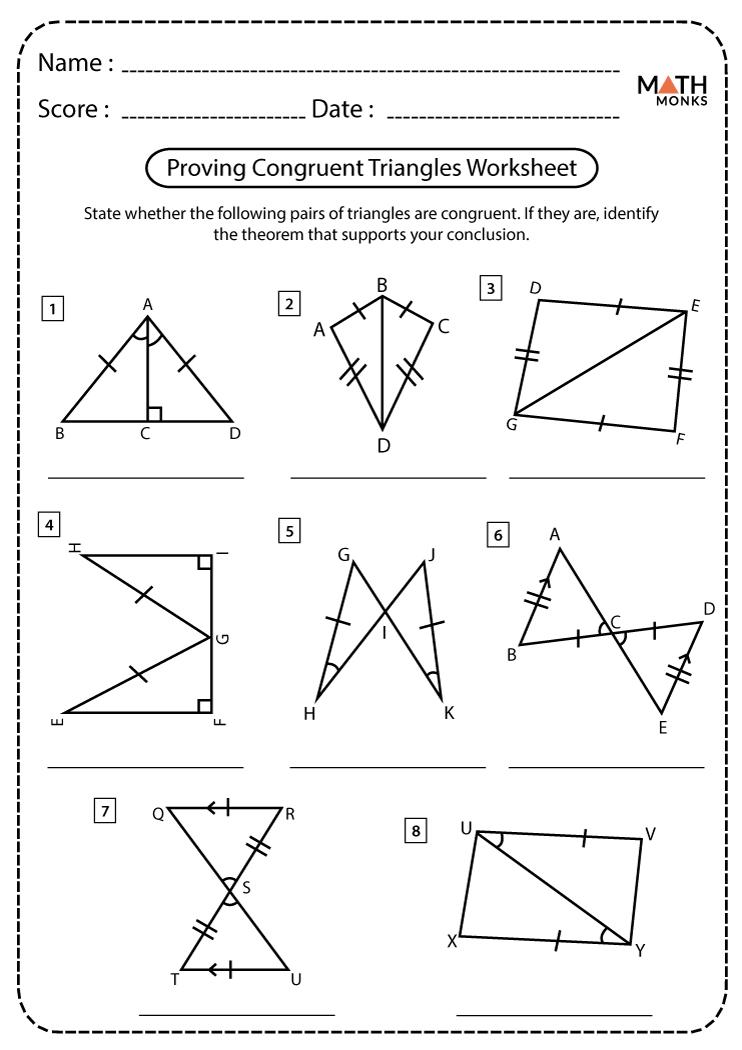
If the worksheet involves proving congruence or constructing congruent triangles:
- Follow the logical steps to prove congruence through known rules.
- For constructions, use tools like compasses and straightedges, keeping the rules in mind.
Tips for Success
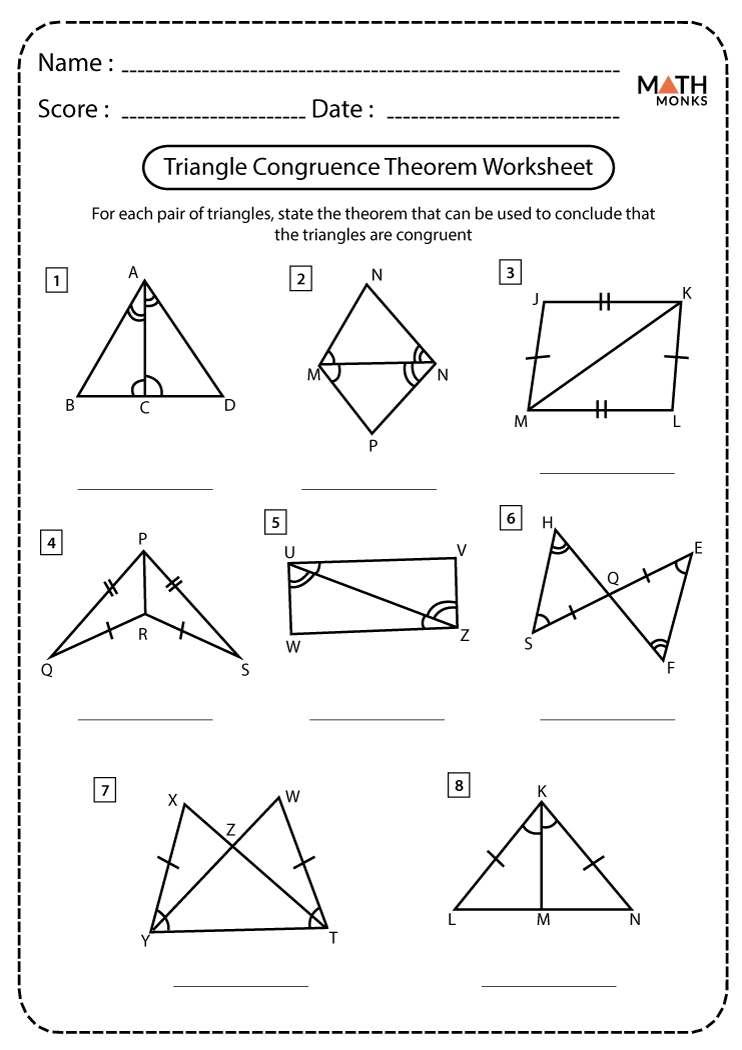
- Practice Regularly: Geometry is highly visual and intuitive; the more you practice, the better you get at recognizing patterns.
- Understand Over Memorize: Instead of memorizing postulates, aim to understand why they work.
- Use Visual Aids: Draw diagrams to help visualize the problem and make decisions based on these sketches.
- Check Your Work: Geometry is meticulous; small errors can lead to wrong conclusions. Always verify your steps.
In wrapping up this exploration into congruent triangles, remember that mastering this concept not only prepares you for more advanced geometric challenges but also sharpens your overall problem-solving skills. Whether in mathematics or real-life scenarios involving design or construction, understanding congruent triangles offers a foundational perspective on how shapes relate and interact in space.
What’s the difference between similarity and congruence?

+
Congruent triangles are identical in both shape and size, whereas similar triangles have the same shape but can differ in size.
Can a triangle be congruent to itself?

+
Yes, a triangle is always congruent to itself, known as the principle of Reflexive Property of Congruence.
How can congruent triangles be used in real life?
+
Congruent triangles are used in fields like architecture for ensuring structural stability, in engineering for design precision, and even in art for maintaining symmetry.
What if the worksheet provides angles but not the sides?
+
If angles are given, you can use ASA or AAS to prove congruence, often along with other geometric properties or constructions to find the sides.