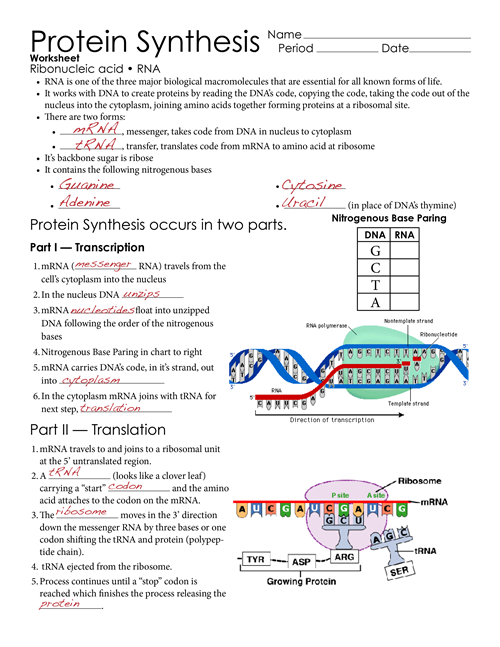
5 Key Methods to Identify Congruent Triangles

In the realm of geometry, understanding how to identify congruent triangles is crucial for both educational pursuits and practical applications. Whether you are a student striving to excel in geometry or an engineer ensuring the integrity of a structure, knowing these methods is indispensable. This post will delve into the 5 key methods to determine if two triangles are congruent, covering everything from simple visual inspections to rigorous mathematical proofs.
1. Side-Side-Side (SSS) Congruence

The first method in our arsenal for identifying congruent triangles is known as the Side-Side-Side (SSS) congruence postulate. Here's how it works:
- Three sides of one triangle are congruent to three sides of another triangle.
- If you can measure three corresponding sides and find them equal in length, then the triangles are congruent.
Consider two triangles ABC and DEF. If:
- AB = DE
- BC = EF
- CA = FD
Then, by the SSS rule, triangle ABC is congruent to triangle DEF.
🔍 Note: It's worth noting that this method is often used when exact measurements are given or when constructing triangles manually.
2. Side-Angle-Side (SAS) Congruence

Another pivotal method for proving triangle congruence is the Side-Angle-Side (SAS) congruence postulate:
- Two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle.
- Here, the angle between the two sides must be measured.
For example, if in triangles XYZ and UVW:
- XY = UV
- YZ = VW
- The angle between XY and YZ (angle Y) is equal to the angle between UV and VW (angle V)
Then, by the SAS rule, triangle XYZ is congruent to triangle UVW.
📐 Note: This method is particularly useful when dealing with isosceles triangles where the equal sides form the included angle.
3. Angle-Side-Angle (ASA) Congruence

Next in our list is the Angle-Side-Angle (ASA) congruence postulate. This method involves:
- Two angles and the included side of one triangle being congruent to two angles and the included side of another triangle.
- The side must be between the two angles.
Suppose in triangles PQR and STU:
- Angle P = Angle S
- Angle Q = Angle T
- PQ = ST
Then, by the ASA rule, triangle PQR is congruent to triangle STU.
4. Angle-Angle-Side (AAS) Congruence

The Angle-Angle-Side (AAS) congruence theorem is a variation of the ASA method, where:
- Two angles and a non-included side of one triangle are congruent to two angles and a corresponding non-included side of another triangle.
- This theorem indirectly leverages the fact that if two angles are the same, the third must be as well (sum of angles in a triangle is always 180 degrees).
For instance, in triangles JKL and MNO:
- Angle J = Angle M
- Angle K = Angle N
- KL = NO
Then, by the AAS rule, triangle JKL is congruent to triangle MNO.
5. Right Angle-Hypotenuse-Side (RHS) Congruence

Finally, we have the Right Angle-Hypotenuse-Side (RHS) congruence theorem, specifically for right-angled triangles:
- If one leg and the hypotenuse of a right triangle are congruent to one leg and the hypotenuse of another right triangle, then they are congruent.
In right triangles with right angles at G and H respectively:
- GH = HI
- The hypotenuse of triangle GHI = the hypotenuse of triangle JKL
Then, by the RHS rule, triangle GHI is congruent to triangle JKL.
In wrapping up, recognizing congruent triangles is not just a mathematical exercise but an essential skill in problem-solving within geometry. Each method provides a distinct approach to proving congruence, ensuring that you have multiple ways to assess and verify the properties of geometric shapes. Whether in school, construction, or beyond, these techniques offer a systematic way to confirm that two shapes can be superimposed onto each other without any distortion.
Can triangles be congruent if only their angles are known?

+
No, knowing only the angles is not sufficient to prove congruence because similar triangles can have different sizes but identical angles.
Is the Angle-Angle-Side (AAS) method always valid?

+
Yes, AAS is a valid method since knowing two angles in a triangle also determines the third angle, making the triangles congruent if a corresponding side is also equal.
What is the difference between congruent and similar triangles?

+
Congruent triangles are identical in all respects (shape and size), whereas similar triangles have the same shape but not necessarily the same size. Similar triangles have corresponding angles equal, but their sides are proportional.