Mastering Congruent Triangles: SSS, SAS, ASA Worksheet Solutions
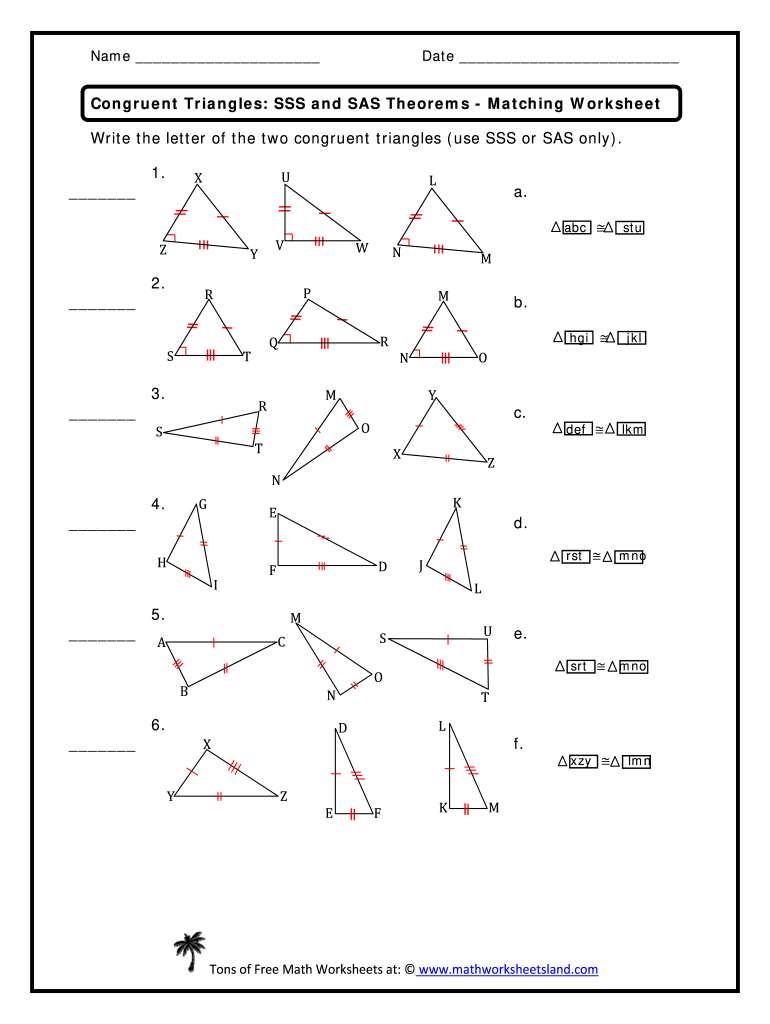
Understanding congruent triangles can be a rewarding challenge for anyone delving into geometry. The study of these triangles not only builds a solid foundation for further geometric inquiry but also teaches us about precision and logical thinking. Today, we'll explore the three most common methods of proving triangles congruent: SSS (Side-Side-Side), SAS (Side-Angle-Side), and ASA (Angle-Side-Angle), with worksheet solutions to bolster your understanding.
What is Congruence?

Two triangles are congruent if their corresponding sides and angles are equal in measure. This means that if you could pick up one triangle and place it on top of the other, they would match perfectly, like two puzzle pieces.

Side-Side-Side (SSS) Congruence

This method proves triangles congruent when all three sides of one triangle are equal in length to the corresponding sides of the other triangle. Here’s how you can apply SSS congruence:
- Identify the sides to be matched in both triangles.
- Confirm that all three pairs of sides are of equal length.
To illustrate, consider the following worksheet solution:
| Triangle ABC | Triangle XYZ | Is Congruent? |
|---|---|---|
| AB = 7 units | XY = 7 units | Yes |
| BC = 10 units | YZ = 10 units | Yes |
| CA = 5 units | ZX = 5 units | Yes |

🔎 Note: Remember, if any one side's length differs, the triangles cannot be congruent by SSS.
Side-Angle-Side (SAS) Congruence
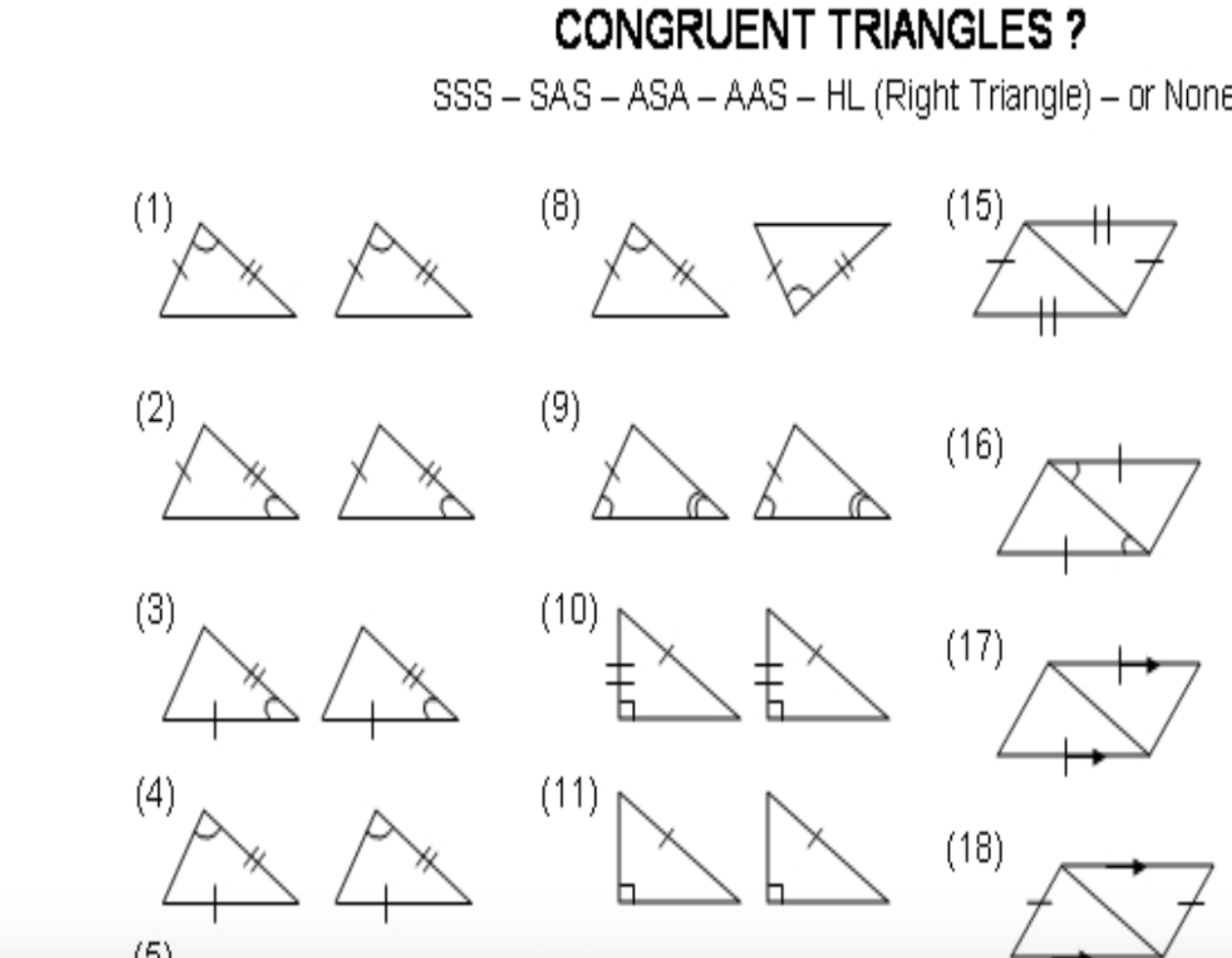
In this method, two sides and the included angle (the angle between those two sides) of one triangle are equal to the corresponding parts of another triangle. Here’s how you prove SAS congruence:
- Identify the two sides and included angle in both triangles.
- Confirm that the sides and angle match.
Here's a worksheet solution applying SAS:
| Triangle PQR | Triangle LMN | Is Congruent? |
|---|---|---|
| PQ = 4 units | LM = 4 units | Yes |
| QR = 5 units | MN = 5 units | Yes |
| ∠PQR = 90° | ∠LMN = 90° | Yes |
Angle-Side-Angle (ASA) Congruence

ASA congruence requires two angles and the included side (the side between the angles) of one triangle to be equal to the corresponding parts of another triangle. The steps to proving ASA congruence are:
- Identify the two angles and included side in both triangles.
- Confirm that the angles and the side match.
Here's a worksheet solution using ASA:
| Triangle JKL | Triangle RST | Is Congruent? |
|---|---|---|
| ∠JKL = 60° | ∠RST = 60° | Yes |
| ∠KJL = 50° | ∠SRT = 50° | Yes |
| KL = 9 units | ST = 9 units | Yes |
🔎 Note: When using ASA, the included side must be between the two angles you're comparing.
How to Improve Your Proof Skills

Practice and visualization are key. Here are some tips:
- Start by sketching triangles and marking known sides and angles.
- Label the triangles to make it easier to identify which parts you are comparing.
- Use statements and reasons in your proof to clarify your logic.
By consistently applying these methods and practicing with various worksheets, you'll grow more confident in recognizing and proving triangle congruence.
Summing up, we've explored three foundational methods of proving triangles congruent: SSS, SAS, and ASA. Each method is unique in its application and requirements for proof. By understanding these principles and practicing with worksheets, you'll enhance your geometric prowess, making you better prepared to tackle complex problems in geometry.
Why do we care about congruent triangles?

+
Congruent triangles are fundamental in geometry because they allow us to prove many geometric theorems and properties, making it easier to solve problems in both theoretical and applied mathematics.
Can a triangle be congruent by SSA?

+
Generally, no. Two triangles with two sides and a non-included angle equal (SSA or “the ambiguous case”) are not necessarily congruent. There can be two different triangles that fit these criteria.
What is the difference between similarity and congruence?

+
Similar triangles have the same shape but not necessarily the same size (all corresponding angles are equal, but sides are proportional). Congruent triangles, however, have both the same shape and size; their corresponding sides and angles are exactly equal.
How can I remember the criteria for congruent triangles?

+
Think of mnemonics like “Three Sides” for SSS, “Two Sides and an Angle” for SAS, and “Two Angles and a Side” for ASA. Visualizing each method can also help in memorizing.



