Congruent Triangles Proofs Worksheet Answers Revealed

Understanding congruent triangles is a cornerstone of geometry that can unlock many doors to geometric proofs and problem-solving in mathematics. In this comprehensive guide, we're going to dive deep into the world of congruent triangles, providing you with not just the answers to common worksheet problems but also an explanation of the underlying principles that govern congruency.
What Makes Triangles Congruent?

Before we delve into proofs and worksheets, let’s first understand the fundamentals:
- Side-Side-Side (SSS) Postulate: If three sides of one triangle are congruent to three sides of another triangle, then the triangles are congruent.
- Side-Angle-Side (SAS) Postulate: If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent.
- Angle-Side-Angle (ASA) Postulate: If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the triangles are congruent.
- Angle-Angle-Side (AAS) Theorem: If two angles and a non-included side of one triangle are congruent to two angles and the corresponding non-included side of another triangle, then the triangles are congruent.
- Hypotenuse-Leg (HL) Theorem: If the hypotenuse and one leg of a right triangle are congruent to the hypotenuse and one leg of another right triangle, then the triangles are congruent.
These principles form the bedrock of congruent triangle proofs.

Congruent Triangles Proofs Worksheet Answers

Let’s now address some common congruent triangles proofs, providing step-by-step solutions to guide you through:
Example 1: Proving Congruence with SAS
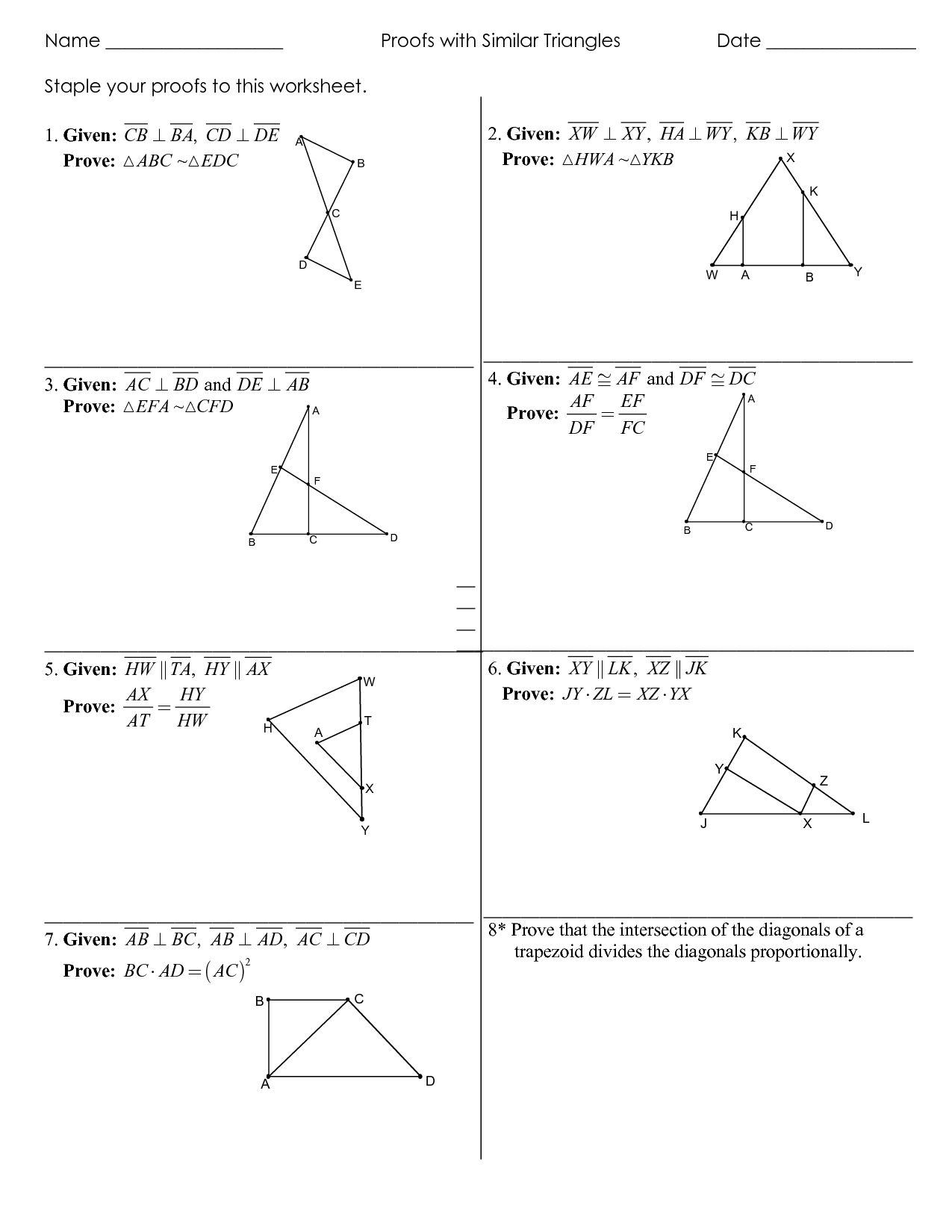
Given:
- BC ≅ EF
- ∠ABC ≅ ∠DEF
- AC ≅ DF
Proof:
- We use the Side-Angle-Side (SAS) Congruence Postulate:
- BC ≅ EF, ∠ABC ≅ ∠DEF, AC ≅ DF
- By the SAS postulate, △ABC is congruent to △DEF.
✏️ Note: Remember to always justify your steps with a postulate or theorem.
Example 2: Using ASA to Prove Congruence

Given:
- AB ≅ DE
- ∠ABC ≅ ∠DEF
- BC ≅ EF
Proof:
- Applying the Angle-Side-Angle (ASA) Postulate:
- AB ≅ DE, ∠ABC ≅ ∠DEF, BC ≅ EF
- Therefore, △ABC ≅ △DEF by ASA.

Example 3: HL Theorem in Right Triangles
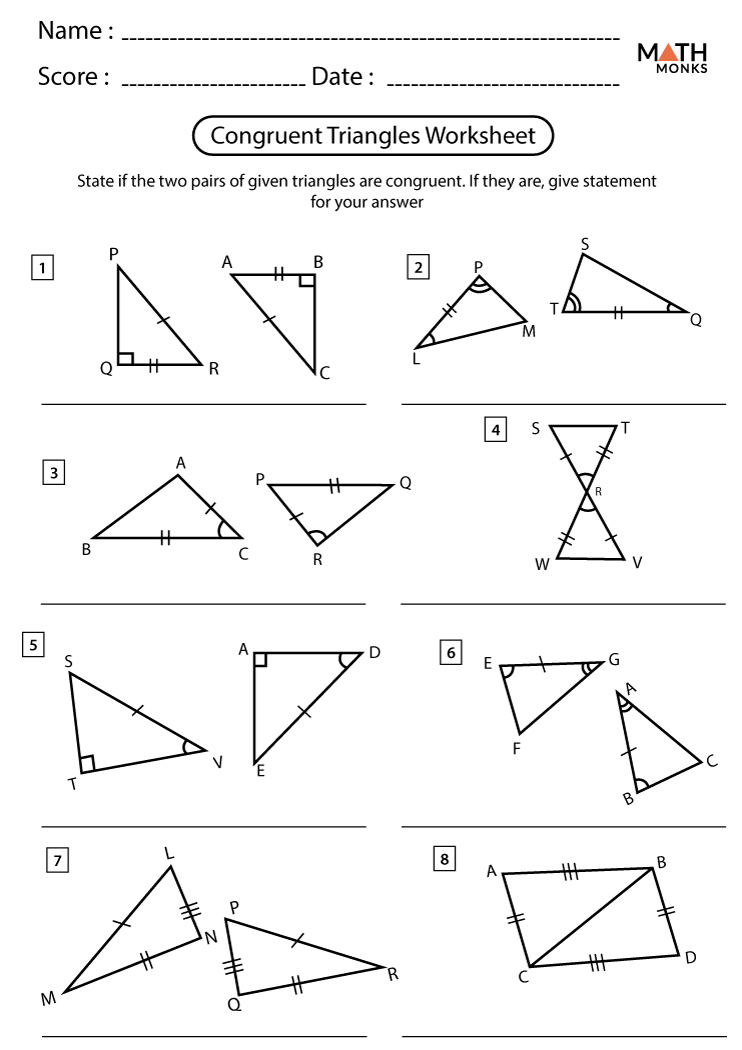
Given:
- △ABC and △DEF are right triangles at C and F, respectively
- AC ≅ DF (hypotenuses)
- BC ≅ EF (one leg)
Proof:
- Since △ABC and △DEF are right triangles, we can apply the Hypotenuse-Leg (HL) Theorem:
- AC ≅ DF, BC ≅ EF
- Thus, △ABC ≅ △DEF by HL.
⚠️ Note: Ensure that the triangles are right triangles before using the HL theorem.
Example 4: Proving Congruence with AAS

Given:
- ∠BAC ≅ ∠EDF
- ∠ABC ≅ ∠DEF
- BC ≅ EF
Proof:
- Applying the Angle-Angle-Side (AAS) Theorem:
- Since two angles and one non-included side are congruent, we can conclude that:
- △ABC ≅ △DEF by AAS.

Example 5: Proving Congruence with SSS

Given:
- AB ≅ DE
- BC ≅ EF
- AC ≅ DF
Proof:
- Using the Side-Side-Side (SSS) Postulate:
- Since all three sides are congruent, we have:
- △ABC ≅ △DEF by SSS.
| Postulate/Theorems | Conditions for Congruency |
|---|---|
| SSS (Side-Side-Side) | All three sides congruent |
| SAS (Side-Angle-Side) | Two sides and the included angle congruent |
| ASA (Angle-Side-Angle) | Two angles and the included side congruent |
| AAS (Angle-Angle-Side) | Two angles and a non-included side congruent |
| HL (Hypotenuse-Leg, for right triangles) | Hypotenuse and one leg congruent |
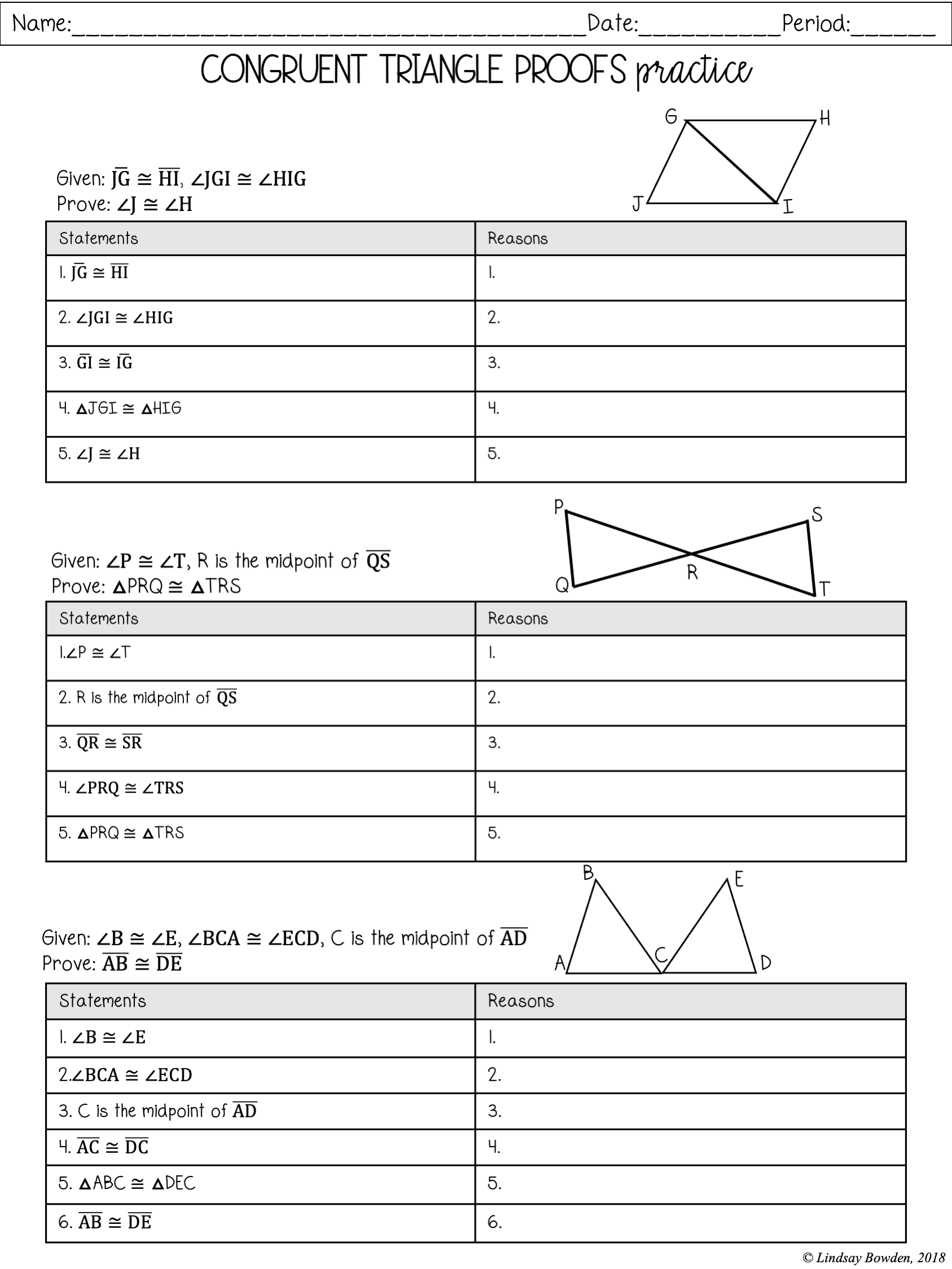
By systematically applying these principles, you can not only solve worksheet problems but also develop a deeper understanding of geometry's logical structure.
In summary, proving congruent triangles involves identifying and using the appropriate congruence postulates or theorems based on the given information. Understanding these principles not only helps in solving specific problems but also enhances your overall grasp of geometry. The examples we've covered illustrate common scenarios you might encounter, and by following these steps, you can confidently prove congruence in your own work.
What is the difference between congruence and similarity?

+
Congruent triangles have the same size and shape, meaning all corresponding sides and angles are equal. Similar triangles have the same shape but not necessarily the same size; their corresponding angles are equal, but the sides are proportional.
Can I use the Angle-Angle (AA) criterion to prove triangles congruent?
+
No, two triangles having two pairs of congruent angles does not guarantee congruence because their sides might differ in length. AA only proves similarity.
How do I know which congruence postulate to use?

+
Examine the given information:
- If three sides are known to be congruent, use SSS.
- If two sides and the included angle are known, use SAS.
- If two angles and the included side are known, use ASA.
- If two angles and a non-included side are known, use AAS.
- For right triangles with congruent hypotenuse and leg, use HL.
What if I only have information on two sides of a triangle?
+
With only two sides congruent, without any angles or the third side being congruent, you cannot prove congruence solely based on those two sides.
Why are proofs important in geometry?

+
Proofs help establish logical reasoning, clarify geometric concepts, and demonstrate the validity of statements or relationships within geometric figures.