Mastering Congruent Triangles: Proofs Worksheet Answers
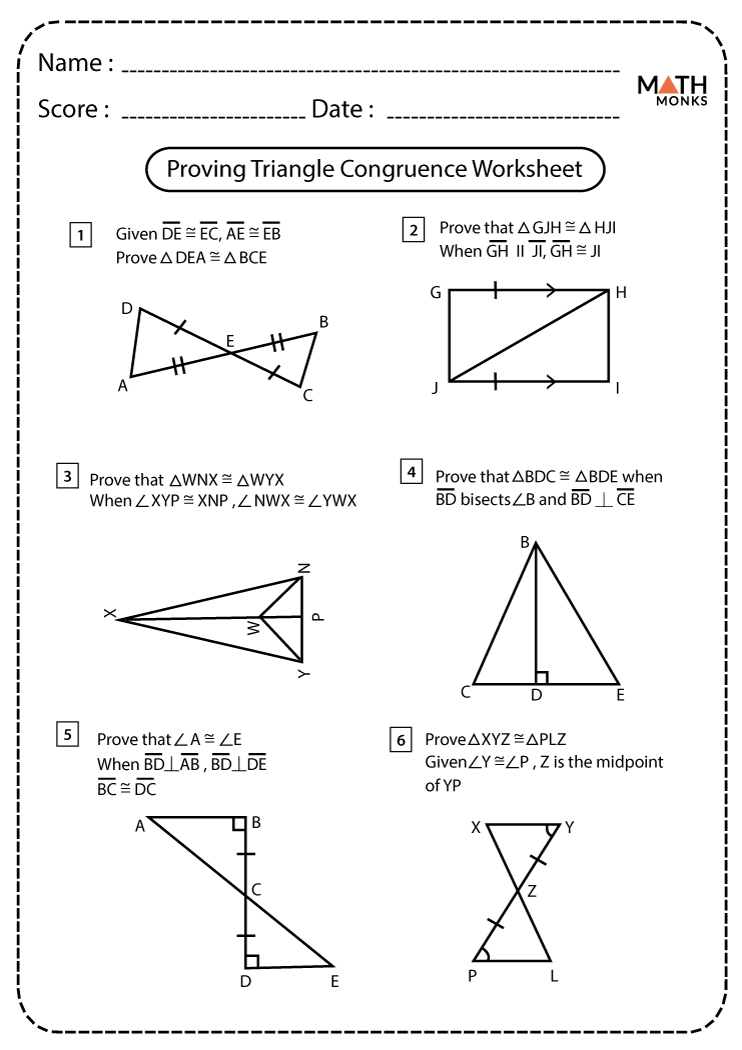
Introduction to Congruent Triangles
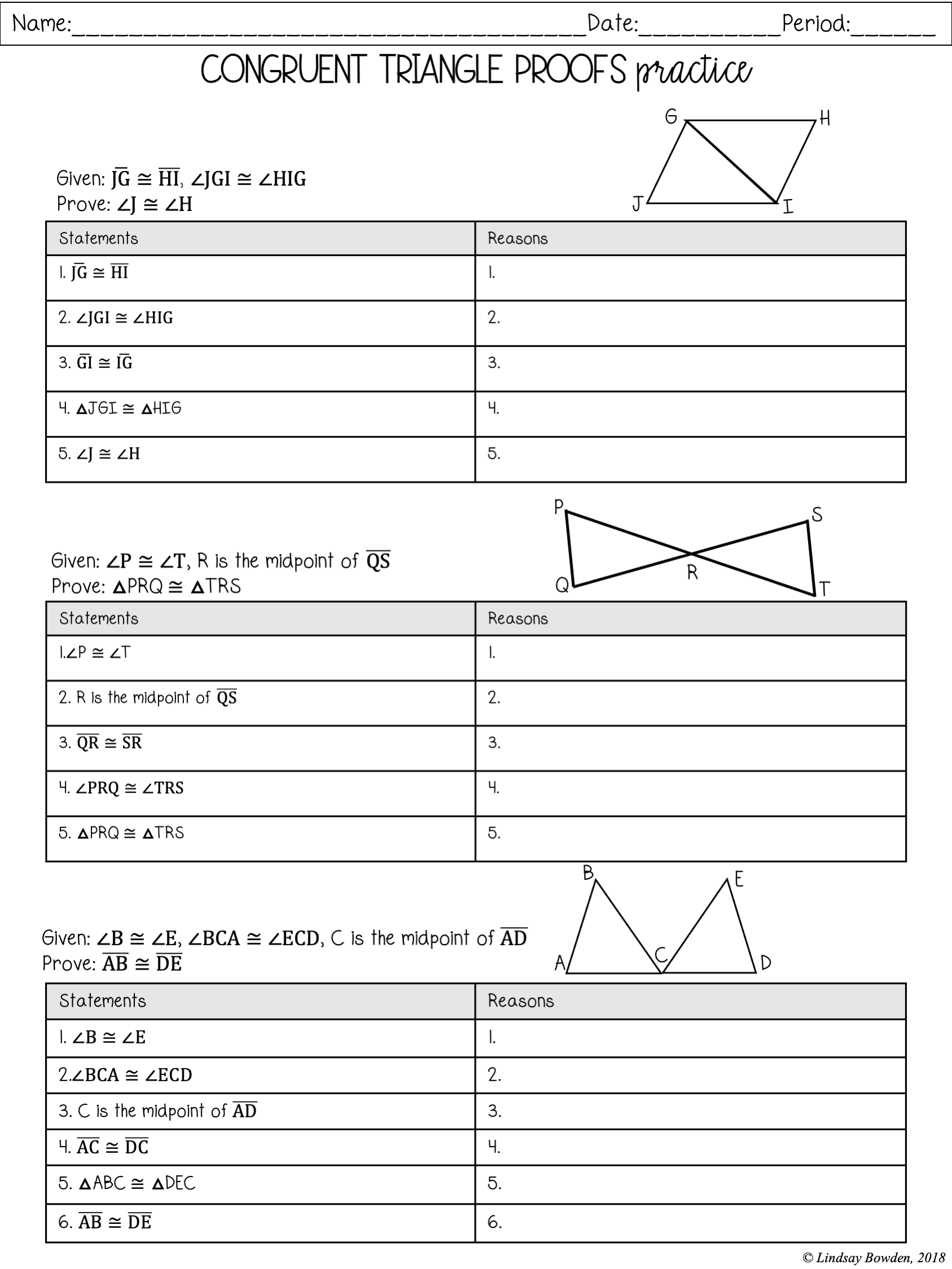
Congruent triangles are a fundamental concept in geometry, forming the basis for understanding various geometric proofs and theorems. When two triangles are congruent, their corresponding sides and angles are equal. This simple but powerful concept allows students and mathematicians to deduce properties of shapes, leading to deeper insights into geometry.
The Basics of Congruent Triangles

To grasp the concept of congruence, let's first understand what makes triangles congruent:
- Side-Side-Side (SSS) Postulate: If three sides of one triangle are equal to the three sides of another triangle, then the triangles are congruent.
- Side-Angle-Side (SAS) Postulate: If two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, the triangles are congruent.
- Angle-Side-Angle (ASA) Postulate: If two angles and the included side of one triangle are equal to two angles and the included side of another triangle, the triangles are congruent.
- Angle-Angle-Side (AAS) Theorem: If two angles and a non-included side of one triangle are equal to two angles and a non-included side of another triangle, the triangles are congruent.
- Hypotenuse-Leg (HL) Theorem: In right triangles, if the hypotenuse and one leg of one triangle are equal to the hypotenuse and one leg of another triangle, then the triangles are congruent.
Proving Congruence: A Step-by-Step Guide

Proving that triangles are congruent involves a systematic approach:
Step 1: Identify Given Information

Start by identifying all the information provided in the problem. This could include:
- Lengths of sides
- Measures of angles
- Other geometric relationships like perpendicularity or parallelism
Step 2: Match Congruent Postulates

Once you have the given information, match it with one of the congruence postulates or theorems:
- If you have three sides (SSS)
- Two sides and the included angle (SAS)
- Two angles and the included side (ASA)
- Two angles and a non-included side (AAS)
- Hypotenuse and a leg in right triangles (HL)
Step 3: Draw Diagrams

Sketch the triangles based on the given information. Label all the known sides and angles accurately. This visual representation helps in conceptualizing the problem.
Step 4: Make Necessary Assumptions

If there are any additional geometric assumptions, mark them on the diagram. For example, if a line is said to be perpendicular to another, show this relationship with a right angle symbol.
Step 5: Use Proof Techniques

Employ various proof techniques like:
- Direct Proof: Start with the given information and use logical steps to show that the triangles are congruent.
- Indirect Proof or Proof by Contradiction: Assume the opposite of what you need to prove, then show that this leads to an impossibility, thereby proving your desired outcome.
Step 6: Write the Proof

Your proof should be concise and logical:
- Begin with the given information or any postulates or definitions used.
- State each step logically, ensuring each follows from the previous.
- Conclude with the statement that the triangles are congruent, followed by the reason for their congruence.
🗒️ Note: When using the AAS or HL theorems, make sure all the conditions are met. Sometimes, problems might require additional geometric properties like vertical angles or properties of isosceles triangles.
Examples of Congruent Triangles Proofs

Let's delve into a couple of examples to see these steps in action:
Example 1: Using SSS Congruence

Given:
- AB = DE
- BC = EF
- CA = FD
Prove: ΔABC ≅ ΔDEF
Proof:
- Given: AB = DE, BC = EF, CA = FD
- By the SSS postulate, since all corresponding sides are equal, ΔABC ≅ ΔDEF.
Example 2: Using SAS Congruence

Given:
- Line segment AB is congruent to line segment DE.
- Angle ABC is congruent to angle DEF.
- Line segment AC is congruent to line segment DF.
Prove: ΔABC ≅ ΔDEF
Proof:
- Given: AB = DE, ∠ABC = ∠DEF, AC = DF.
- By the SAS postulate, ΔABC ≅ ΔDEF.
✅ Note: Be cautious when using SAS or ASA; make sure the included angle or side is correct to avoid common errors.
Advanced Techniques in Proving Congruence
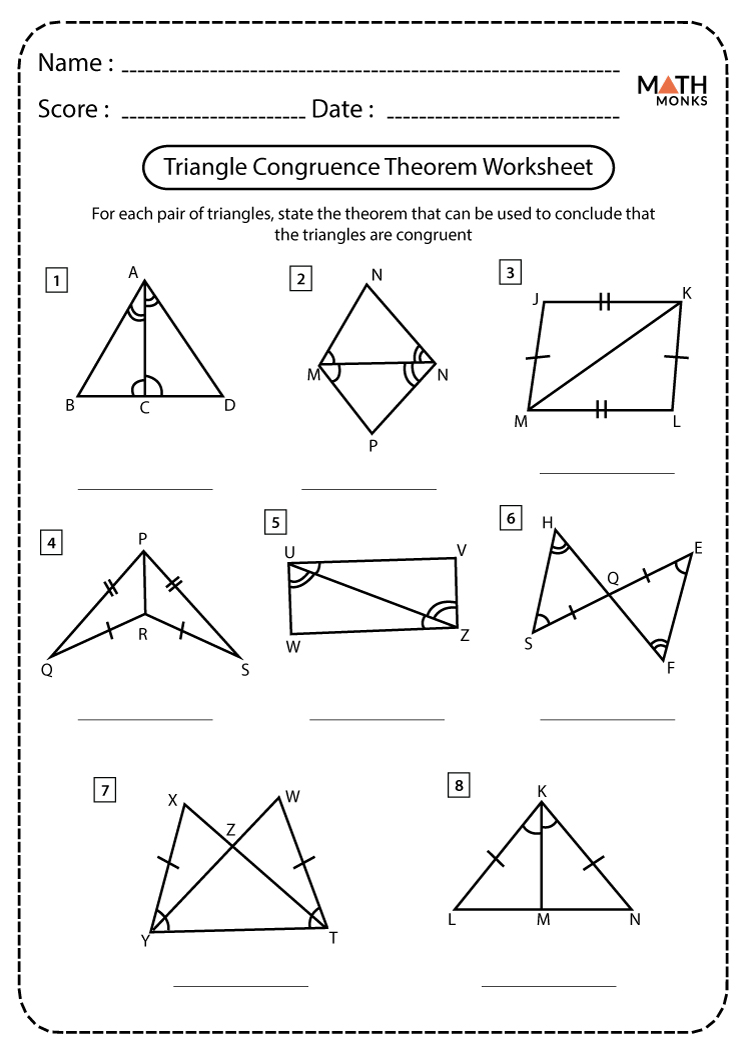
While the basic methods are straightforward, here are some advanced techniques for more complex proofs:
- Using Midpoints: If a line segment bisects another line segment into two equal parts, this can be used to prove congruent triangles by creating isosceles triangles.
- Coordinate Geometry: Use coordinates to establish congruence by showing that distances between points are equal.
- Transformation Geometry: Utilize reflections, rotations, or translations to establish congruence.
- Angle Bisector Theorem: If an angle bisector splits a triangle, the two triangles created by it are congruent.
The Importance of Congruent Triangles in Geometry

Congruent triangles serve as a cornerstone in geometric proofs:
- Property Deduction: Congruence allows us to deduce properties of shapes, which is crucial in understanding and proving geometric theorems.
- Constructing Proofs: Many advanced geometric proofs rely on congruent triangles as a starting point or intermediate step.
- Real-World Applications: Understanding congruence helps in fields like architecture, where similar structures are designed to be congruent for functionality or aesthetics.
The ability to prove triangle congruence not only enhances your geometric intuition but also equips you with critical thinking skills that transcend mathematics into real-world problem-solving.
In summary, mastering the proofs of congruent triangles involves understanding the fundamental postulates, applying them systematically in logical proofs, and being aware of advanced techniques when simpler methods fail. By mastering this topic, you'll be well-prepared to tackle more complex geometry problems and appreciate the beauty and utility of mathematical proofs.
What is the difference between congruence and similarity in triangles?

+
Congruence means that two triangles are exactly the same in every respect (all corresponding sides and angles are equal). Similarity, on the other hand, means that the triangles have the same shape but not necessarily the same size; corresponding angles are equal, but sides are in proportion.
Why are congruent triangles important in real-world applications?
+
Congruent triangles are crucial in engineering, architecture, and design where exact dimensions are necessary. They ensure that structures and components fit together correctly, maintain symmetry, or ensure uniformity in parts production.
Can you prove congruence with just two sides and one angle?
+If the angle is between the two sides (SAS), yes, you can prove congruence. However, if the angle is not included or is opposite to one of the sides (like SSA), you cannot always prove congruence because there can be two non-congruent triangles with these properties (ambiguous case).



