7 Engaging Worksheets to Master Congruent Triangles
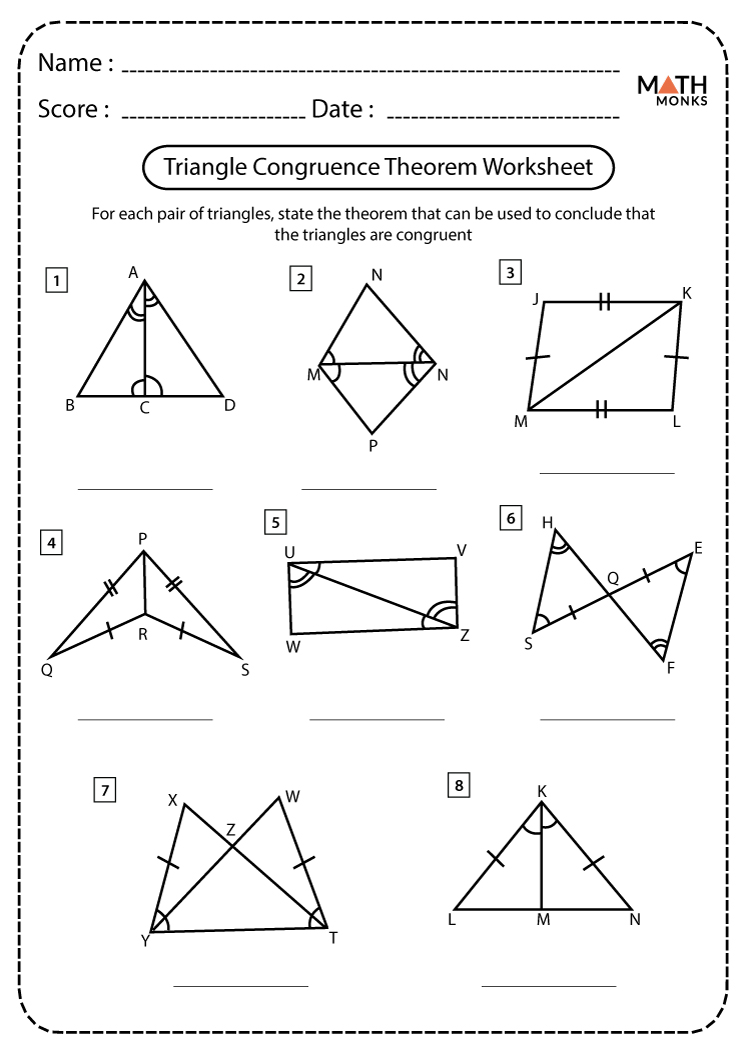
In the field of geometry, understanding congruent triangles can significantly enhance one's ability to solve geometric problems and understand spatial relationships. This deep dive into congruent triangles, supported by interactive worksheets, not only bolsters mathematical proficiency but also makes learning fun and engaging.
What Are Congruent Triangles?
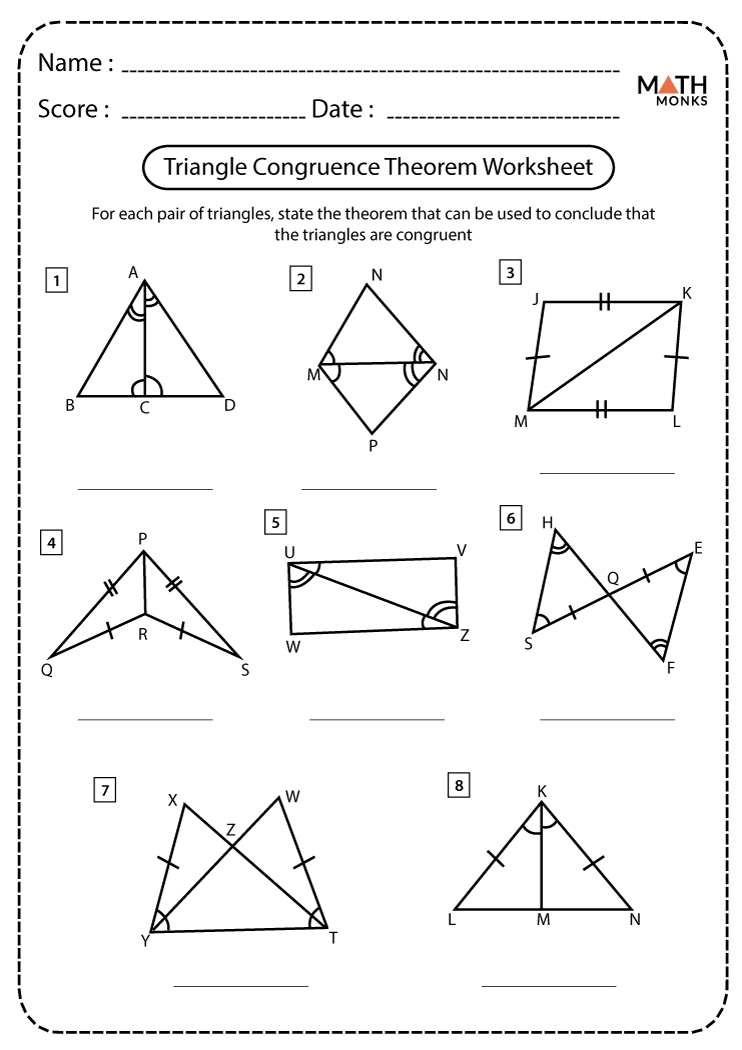

At its core, congruence in triangles means that two triangles are identical in shape and size, fitting perfectly on top of one another if overlaid. This equality is determined by matching sides or angles according to the following principles:
- SSS (Side-Side-Side): All three sides are equal.
- SAS (Side-Angle-Side): Two sides and the included angle are equal.
- ASA (Angle-Side-Angle): Two angles and the included side are equal.
- AAS (Angle-Angle-Side): Two angles and a non-included side are equal.
- RHS (Right-angle-Hypotenuse-Side): Applies to right triangles where the hypotenuse and one other side are equal.
Why Use Worksheets?
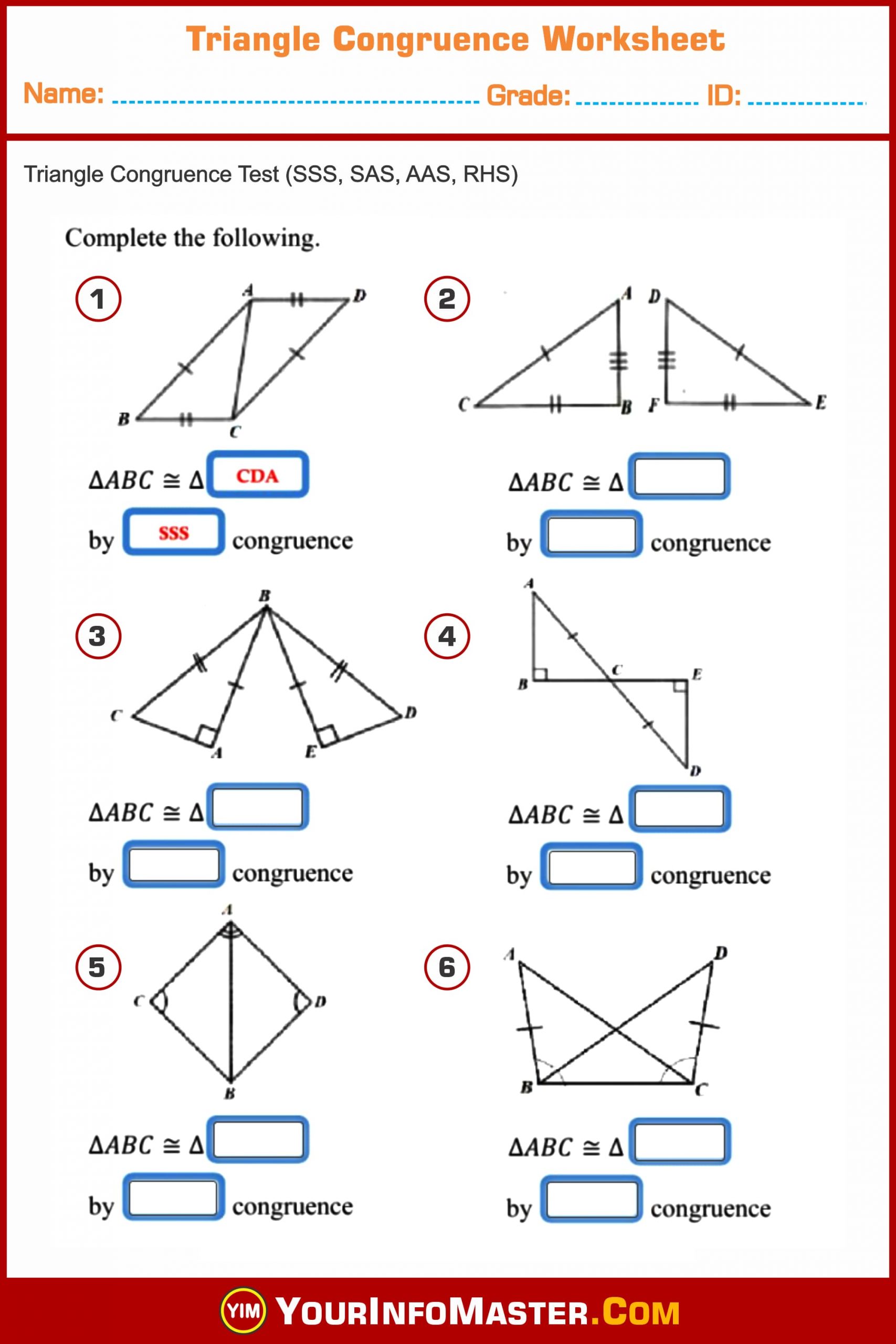
Worksheets are a valuable tool for:
- Practicing the concepts through repetition.
- Visualizing how congruence proofs work.
- Helping to identify common mistakes in geometric reasoning.
- Providing immediate feedback for correction and understanding.
7 Engaging Worksheets for Mastering Congruent Triangles

1. Identify and Label Triangles

Start with basic exercises where students are given triangles with sides or angles labeled. The goal is to identify which triangles are congruent based on the given criteria. This worksheet helps in:
- Understanding the importance of labeling in proofs.
- Recognizing the different methods of proving congruence.
2. Congruence Proofs Practice

This worksheet is designed for students to practice writing proofs of congruence. Here’s what to expect:
- Given two triangles, students must prove they are congruent using a given or deduced set of data.
- It encourages critical thinking and logical structuring of information.
3. Cut and Match Congruent Triangles

A hands-on activity where students physically cut out triangles and try to match them with congruent counterparts. This exercise:
- Makes abstract concepts tangible.
- Teaches students to visualize and match triangles accurately.
4. Angle Bisector and Altitude Work

By exploring angles and segments created by bisectors and altitudes, this worksheet introduces:
- How to use bisectors and altitudes in congruence proofs.
- Application of theorems related to triangles’ midlines and perpendiculars.
5. Indirect Proofs

This worksheet focuses on proving congruence indirectly:
- Students assume triangles are not congruent and find contradictions to prove they must be.
- It’s an advanced technique that teaches logical reasoning and problem-solving.
6. Crossword Puzzle for Vocabulary

A creative approach to learn and reinforce:
- Terms like “congruent,” “isosceles,” “equilateral,” etc.
- Enhances vocabulary retention and makes learning less daunting.
7. Real-World Applications
Applying congruence to practical scenarios:
- Students work on problems where triangle congruence principles help in solving real-world geometry problems.
- This connects classroom learning to everyday life.
📝 Note: Ensure each worksheet has a clear set of instructions, key, and examples to guide students through the exercises.
In this comprehensive exploration of congruent triangles, students gain not only theoretical knowledge but also practical skills to manipulate and understand these shapes. The use of diverse and engaging worksheets ensures that learning is interactive, visual, and effective, providing a solid foundation for more advanced geometric concepts.
To sum up, mastering congruent triangles through these targeted worksheets enriches students' geometric understanding. It prepares them for more complex topics in geometry, while making the learning process an enjoyable and interactive journey.
What are the key differences between congruent triangles and similar triangles?

+
Congruent triangles have the same size and shape, meaning all corresponding sides and angles are equal. Similar triangles, on the other hand, have the same shape but can be different in size. Their corresponding angles are equal, but their sides are proportional.
Can triangles be congruent if they are not of the same type (e.g., isosceles, scalene)?

+
Yes, triangles can be congruent even if they are different types as long as they meet the congruence criteria like SSS, SAS, ASA, AAS, or RHS. The specific type does not matter if the given sides or angles match.
How can students check if they’ve correctly identified congruent triangles?

+
They can use a simple overlay method with cut-out triangles or use the congruence postulates to logically prove the congruence through step-by-step reasoning. If all corresponding sides or angles match, then the triangles are congruent.