Mastering Congruent Triangles: Proofs Worksheet with Answers

If you are delving into the realm of geometry, particularly the topic of congruent triangles, mastering the art of proofs is fundamental. This comprehensive guide will walk you through the intricacies of congruent triangle proofs, providing you with detailed worksheets, answers, and strategic tips to enhance your understanding and problem-solving skills.
Understanding Congruence and Triangles

To start, let’s clarify what congruence means in geometry:
- Congruence: Two geometric figures are congruent if they have exactly the same size and shape. For triangles, this means all corresponding sides and angles are equal.
Here are the primary methods for proving triangles congruent:
- Side-Side-Side (SSS) Congruence Postulate: If all three sides of one triangle are equal to the three sides of another, the triangles are congruent.
- Side-Angle-Side (SAS) Congruence Postulate: If two sides and the included angle of one triangle are equal to two sides and the included angle of another, the triangles are congruent.
- Angle-Side-Angle (ASA) Congruence Postulate: If two angles and the included side of one triangle are equal to two angles and the included side of another, the triangles are congruent.
- Angle-Angle-Side (AAS) Congruence Theorem: If two angles and a non-included side of one triangle are equal to two angles and a non-included side of another, the triangles are congruent.
- Right Angle-Hypotenuse-Side (RHS or HL) Congruence Theorem: For right triangles, if the hypotenuse and one leg of one right triangle are congruent to the hypotenuse and a leg of another, the triangles are congruent.
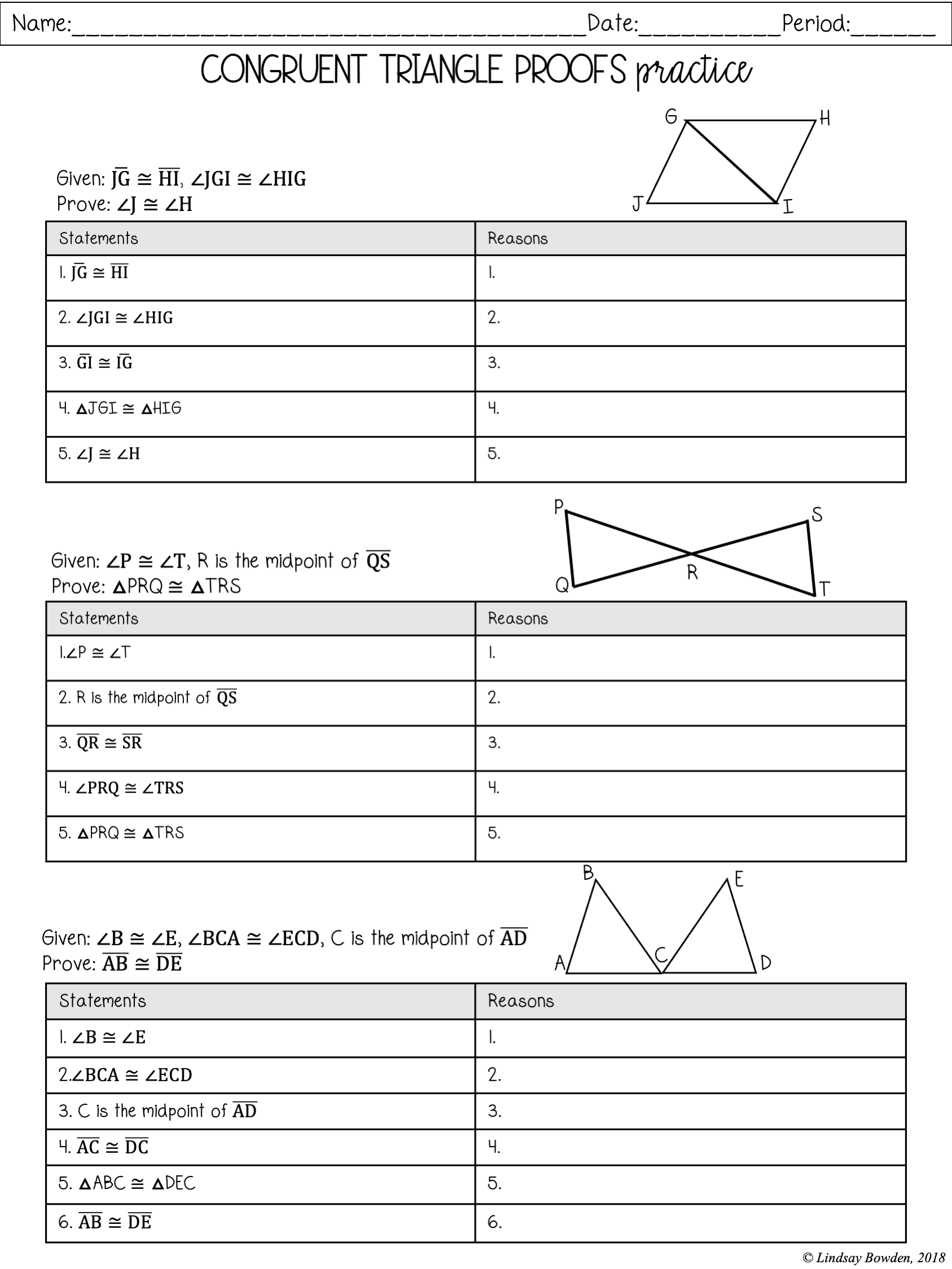
Proofs Worksheet for Congruent Triangles

Below is an example of a congruent triangle proof worksheet designed to enhance your skills:

| Statement | Reason |
|---|---|
| 1. AB \cong DE | Given |
| 2. AC \cong DF | Given |
| 3. BC \cong EF | Given |
| 4. \triangle ABC \cong \triangle DEF | SSS Congruence Postulate |

Here, the proof uses the SSS Congruence Postulate to prove that the triangles are congruent.
🔍 Note: Each step in a geometric proof must be logically connected and based on a postulate, theorem, or given information.
Strategies for Proof Construction

When constructing a proof:
- Analyze Given Information: Identify all given data, including congruent sides, angles, and any parallel or perpendicular lines.
- Draw Diagrams: Sketch out the problem. Diagrams help visualize the problem, which can make solving proofs much simpler.
- Determine Congruence Criteria: Decide which congruence postulate or theorem fits the given information best.
- Make Logical Deductions: Deduce additional congruent sides or angles using properties or theorems.
Example Proofs with Detailed Steps

Example 1: Using SAS Postulate

Given:
- Triangle ABC and DEF
- (AB \cong DE)
- (\angle BAC \cong \angle EDF)
- (AC \cong DF)
Proof:
| Statement | Reason |
|---|---|
| 1. AB \cong DE | Given |
| 2. \angle BAC \cong \angle EDF | Given |
| 3. AC \cong DF | Given |
| 4. \triangle ABC \cong \triangle DEF | SAS Congruence Postulate |
Key Takeaways from Example:
- Two sides and the included angle determine the triangle's shape uniquely.
- Proper use of given information and the SAS Congruence Postulate can lead to proving congruence efficiently.
🔎 Note: When proving congruence with angles, make sure they are included angles, or use a different criterion like AAS.
Example 2: Using AAS Theorem

Given:
- Triangle ABC and DEF
- (\angle A \cong \angle D)
- (\angle B \cong \angle E)
- (BC \cong EF)
Proof:
| Statement | Reason |
|---|---|
| 1. \angle A \cong \angle D | Given |
| 2. \angle B \cong \angle E | Given |
| 3. BC \cong EF | Given |
| 4. \triangle ABC \cong \triangle DEF | AAS Congruence Theorem |
Strategies from Example:
- AAS is useful when given two angles and a non-included side.
- Check if the given information aligns with the theorem before applying it.
In summary, these examples illustrate different strategies for constructing proofs and highlight the importance of recognizing which congruence criteria to apply based on the given information. Through consistent practice with such proofs, you'll improve your geometrical intuition and problem-solving skills, which are essential for mastering mathematics and advanced geometric studies.
What is the difference between congruence and similarity?
+
Congruence means two figures are the same shape and size, whereas similarity means they have the same shape but can be of different sizes.
Can we use CPCTC (Corresponding Parts of Congruent Triangles are Congruent) to prove the congruence of triangles?

+
CPCTC is not used to prove triangles are congruent; rather, it is a consequence of triangle congruence. Once triangles are proven congruent, corresponding parts can be declared congruent.
Why is the SAS postulate not working with right triangles?

+
In right triangles, the hypotenuse or a leg is usually not the included angle or side, so SAS is typically not used; instead, the RHS theorem is applied.