Master Congruence with Our Easy Worksheet Guide
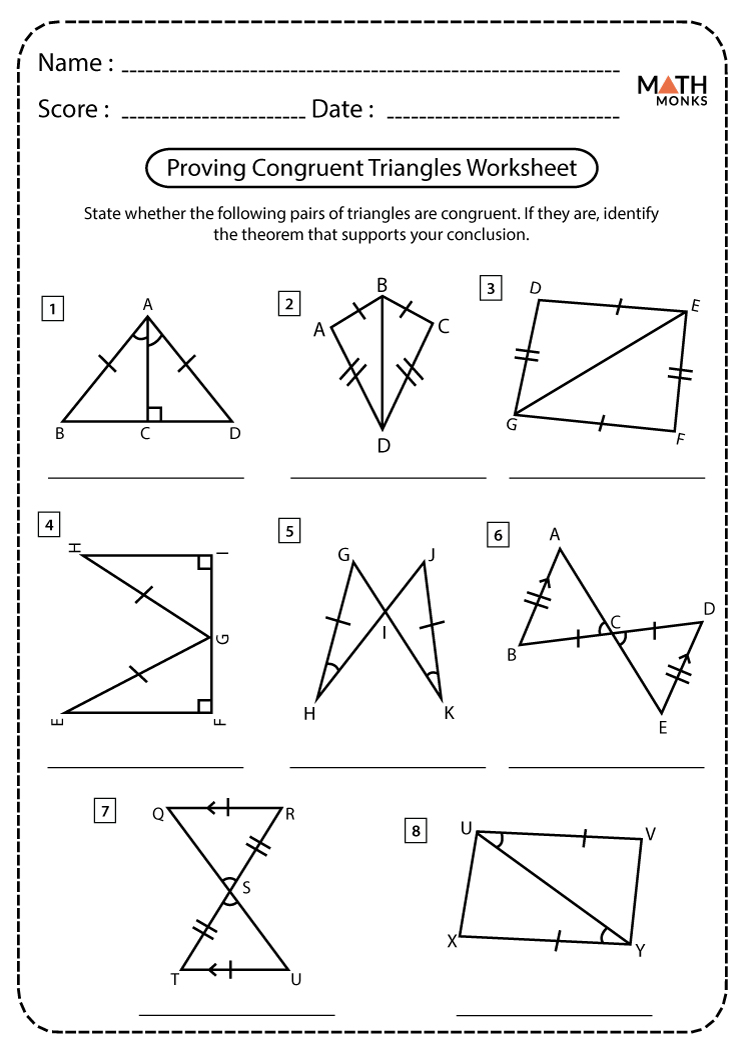
In the mathematical realm, congruence stands as a pivotal concept, offering a bridge between algebra and arithmetic. Whether you're diving into number theory or tackling algebraic structures, understanding congruence provides a foundational layer for a myriad of calculations and theories. Today, we'll explore how to master this principle with an easy-to-follow worksheet guide, ensuring you grasp not just the fundamentals but also its practical applications.
What is Congruence?

Congruence, denoted by the symbol ≡, refers to the relationship between two integers that have the same remainder when divided by another integer. If a and b are integers and n is a positive integer, then a is congruent to b modulo n if:
- a ≡ b (mod n) if and only if n divides a - b.
Imagine having integers 7 and 23. If we consider modulus 5, both 7 and 23 leave a remainder of 2 when divided by 5. Hence, we say 7 ≡ 23 (mod 5).
🔍 Note: Understanding the base concept of divisibility is key before diving into congruence.
Worksheet to Master Congruence

Here's a structured worksheet that can help you practice and understand congruence:
| Problem | Solution Steps |
|---|---|
| Find if 17 ≡ 2 (mod 5). | Check the remainder of 17 and 2 when divided by 5: 17 divided by 5 gives a remainder of 2, and 2 divided by 5 gives a remainder of 2. Therefore, 17 ≡ 2 (mod 5) is true. |
| Is 25 ≡ 10 (mod 3)? | Check remainder: 25 divided by 3 gives 1, 10 divided by 3 gives 1. Hence, 25 ≡ 10 (mod 3) is true. |
| Determine if 9 ≡ 16 (mod 7). | Check the remainders: 9 divided by 7 gives 2, and 16 divided by 7 gives 2. So, 9 ≡ 16 (mod 7) holds. |

Using Congruence in Algebra

Congruence finds significant applications in algebra, particularly in solving linear congruences:
- Example: Solve x ≡ 3 (mod 5).
- The solutions are all numbers that leave a remainder of 3 when divided by 5. These include 3, 8, 13, 18, and so on.
Congruence Classes and Equivalence

When you understand that two numbers are congruent modulo n, you're essentially saying they belong to the same congruence class. Here's how to visualize this:
- All integers can be divided into equivalence classes where each class consists of numbers that are congruent modulo n.
- For example, for modulo 3, you have three classes: [0], [1], and [2].
🧠 Note: These classes form an algebraic structure known as a ring which is fundamental in abstract algebra.
Practical Applications

Congruence's real-world applications are both profound and numerous:
- Cryptography: Modern encryption algorithms like RSA rely heavily on congruence calculations.
- Computer Science: Hash tables use modular arithmetic for mapping keys to indexes in arrays.
- Error Detection: ISBN and UPC codes use congruences to detect transcription errors.
Final Reflections

Mastering congruence through practice and understanding opens up vast mathematical landscapes. From cryptographic protocols to the structure of algebraic systems, congruence serves as both a tool and a lens through which to view numbers. This worksheet guide is just a starting point; each problem solved adds layers to your mathematical foundation, offering a path through algebra, number theory, and beyond. Let this be your guide to not only understanding but also appreciating the beauty of mathematical structure and patterns.
What is the simplest example of congruence?
+
The simplest example would be 5 ≡ 1 (mod 4), where 5 and 1 both have the same remainder when divided by 4.
Can congruence relations be used in everyday life?
+
Yes, congruence relations appear in scheduling, for example, when arranging recurring events where the intervals are multiples of some period.
How does learning congruence help in understanding larger mathematical structures?
+
Understanding congruence introduces the idea of equivalence classes, which are foundational in abstract algebra, leading to groups, rings, and fields.