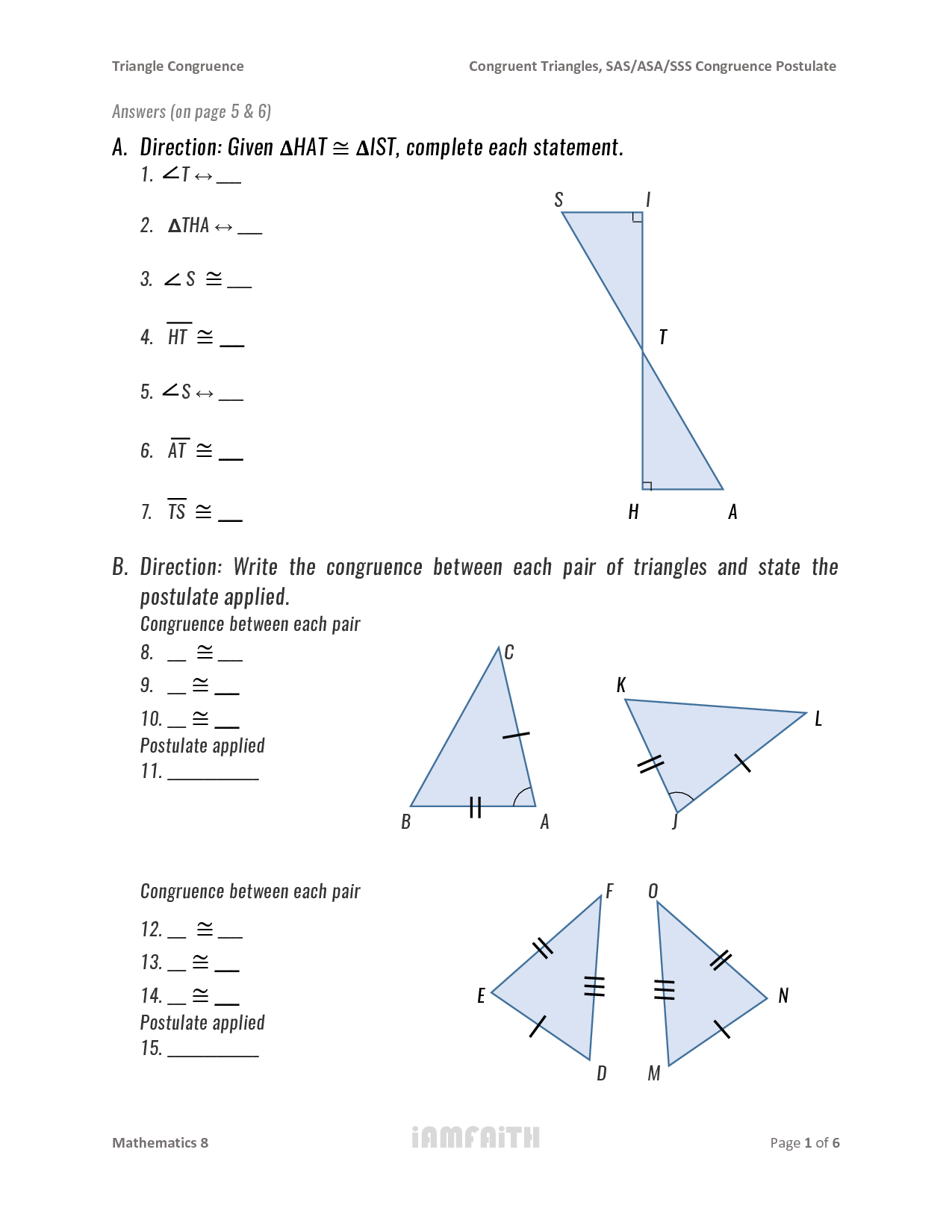
Master Congruence Postulates with Our Handy Worksheet
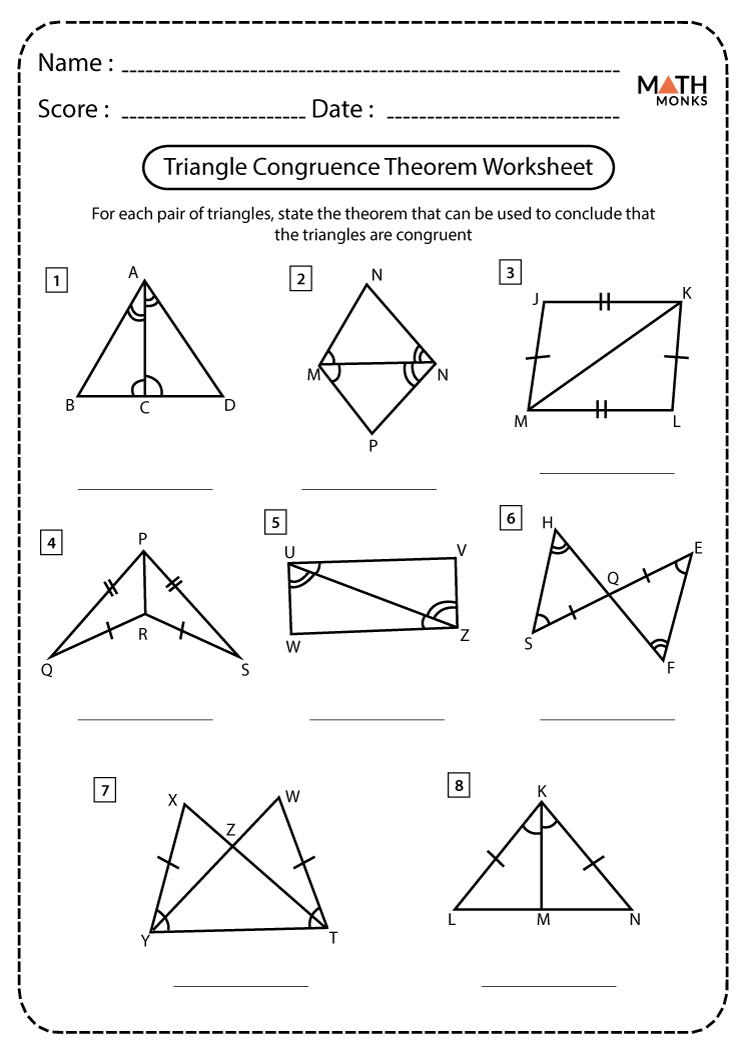
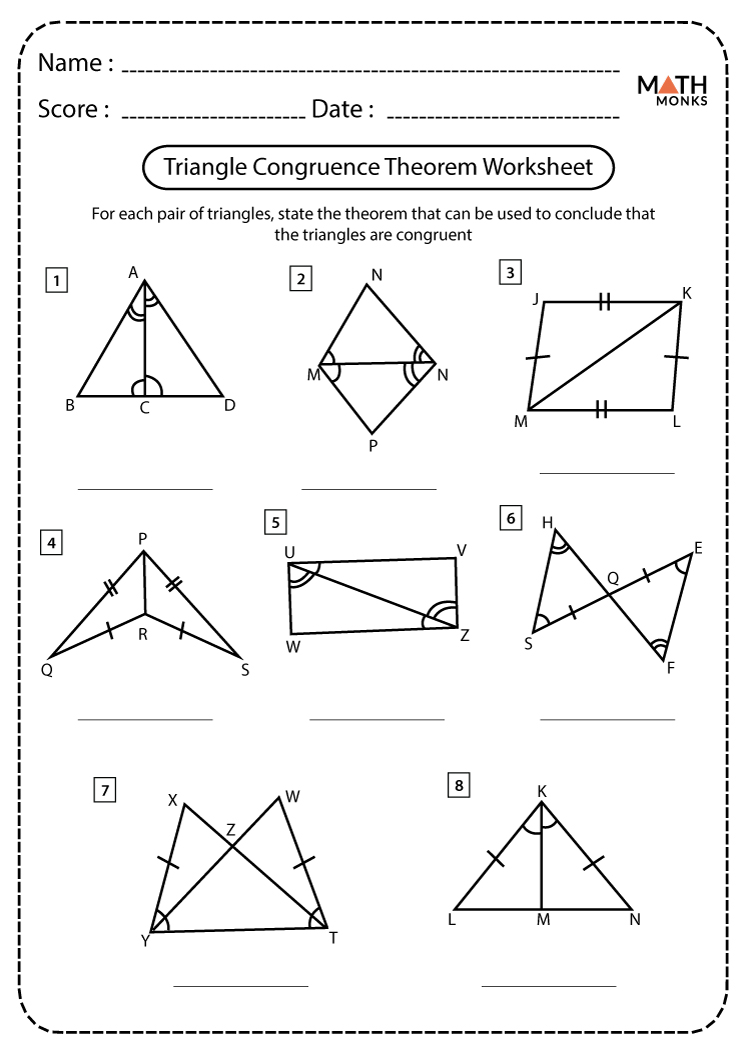
The concept of congruence plays a pivotal role in geometry, serving as the foundation for understanding shapes, symmetry, and spatial relationships. Congruence involves figures that are identical in size and shape, and exploring this concept through congruent triangles is particularly insightful. This post will guide you through various congruence postulates—namely Side-Side-Side (SSS), Side-Angle-Side (SAS), Angle-Side-Angle (ASA), and Hypotenuse-Leg (HL) for right triangles—while providing practical examples through a worksheet to reinforce your learning.
Understanding Congruence Postulates

Congruence postulates are rules that, when satisfied, allow us to deduce that two triangles are congruent. Here’s a look at each:
- SSS (Side-Side-Side): If all three sides of one triangle are equal in measure to the three sides of another triangle, the triangles are congruent.
- SAS (Side-Angle-Side): If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, they are congruent.
- ASA (Angle-Side-Angle): If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, they are congruent.
- HL (Hypotenuse-Leg): For right triangles, if the hypotenuse and one leg of one triangle are congruent to the hypotenuse and one leg of another triangle, they are congruent.
SSS Postulate: The Basics
The SSS postulate is often considered the simplest since it relies solely on the sides:
- If ∆ABC has sides a, b, and c, and ∆DEF has sides d, e, and f such that a = d, b = e, and c = f, then ∆ABC ≡ ∆DEF.
| Triangle ABC | Triangle DEF |
|---|---|
| a = 5 | d = 5 |
| b = 6 | e = 6 |
| c = 7 | f = 7 |
SAS Postulate: The Angle and Sides

The SAS postulate incorporates the angle between two sides, adding an element of directionality:
- If ∆ABC has sides AB = DE, AC = DF, and angle BAC = angle EDF, then ∆ABC ≡ ∆DEF.
ASA Postulate: Angles and Their Included Sides
With ASA, congruence is established through two angles and the side between them:
- If ∆ABC has angles ∠BAC = ∠EDF, ∠ABC = ∠DEF, and side BC = EF, then ∆ABC ≡ ∆DEF.
HL Postulate: Right Triangles

HL applies specifically to right triangles:
- If ∆ABC has a right angle at C, with AC as the hypotenuse and AB as a leg, and ∆DEF has a right angle at F, with DF as the hypotenuse and DE as a leg, and if AC = DF and AB = DE, then ∆ABC ≡ ∆DEF.
Practical Application: Congruence Worksheet

To better understand these concepts, let’s delve into a worksheet with examples:
Exercise 1:

Given the following triangles:
- ∆XYZ with sides XY = 6 cm, YZ = 8 cm, and XZ = 10 cm
- ∆LMN with sides LM = 6 cm, MN = 8 cm, and LN = 10 cm
Determine if they are congruent, and by which postulate.
Answer: ∆XYZ and ∆LMN are congruent by SSS postulate since all corresponding sides are equal.
Exercise 2:
Given the following triangles:
- ∆PQR with sides PQ = 9 cm, QR = 10 cm, and ∠PQR = 53°
- ∆STU with sides ST = 9 cm, TU = 10 cm, and ∠STU = 53°
Determine if they are congruent, and by which postulate.
Answer: ∆PQR and ∆STU are congruent by SAS postulate since two sides and the included angle are congruent.
📚 Note: When identifying congruence postulates, remember to use the given information. When a triangle's dimensions are described in units like 'cm,' ensure you compare like units.
Exercise 3:

Given the following triangles:
- ∆XYZ with ∠YXZ = 45°, ∠XZY = 30°, and side XZ = 5 cm
- ∆ABC with ∠BAC = 45°, ∠ACB = 30°, and side AC = 5 cm
Determine if they are congruent, and by which postulate.
Answer: ∆XYZ and ∆ABC are congruent by ASA postulate since two angles and the included side are congruent.
Recap and Next Steps

The exploration of congruence postulates opens up a world of problem-solving and geometric relationships. By mastering these postulates through worksheets and real-world applications, you not only enhance your understanding of triangles but also build a foundation for more complex geometric proofs. Remember:
- SSS involves all sides.
- SAS includes an angle and two sides.
- ASA focuses on angles and the included side.
- HL applies to right triangles only.
Keep practicing, and soon, these postulates will become second nature, allowing you to tackle more intricate geometry problems with confidence.
What is the difference between congruence and similarity?

+
Congruence means two shapes are identical in both size and shape. Similarity, on the other hand, means the shapes are the same except for their size. They might be scaled versions of each other but not necessarily the same size.
Can two triangles be congruent if they only have two sides equal?

+
Two triangles cannot be proven congruent with just two equal sides unless you also know the angles between them (SAS) or if one of the angles is a right angle and you know the hypotenuse (HL for right triangles).
Why is the HL postulate limited to right triangles?
+
The HL postulate is specific to right triangles because the right angle forms a unique configuration where the hypotenuse, along with one leg, fully determines the triangle’s shape and size.