5 Ways to Master Geometry: Conditional Statements Worksheet

In the study of mathematics, geometry stands out as a particularly fascinating subject due to its practical applications and the abstract beauty of its theorems and proofs. Mastering geometry requires not only understanding its fundamental concepts but also mastering the art of logical reasoning through conditional statements. Here, we explore five effective strategies to excel in geometry, focusing on the use of conditional statements worksheets, which are invaluable tools for developing your geometric intuition and proof-writing skills.
1. Understanding Conditional Statements
Before diving into worksheets, it’s crucial to understand what a conditional statement is in the context of geometry. A conditional statement or an if-then statement, follows the form “If P, then Q,” where P is called the hypothesis, and Q is the conclusion. Here are the key elements:
- Hypothesis (P): This is the condition or the “if” part of the statement.
- Conclusion (Q): This is what happens or is true if the hypothesis holds.
Understanding the structure and implications of conditional statements can help in identifying given facts and what needs to be proven in geometric problems.
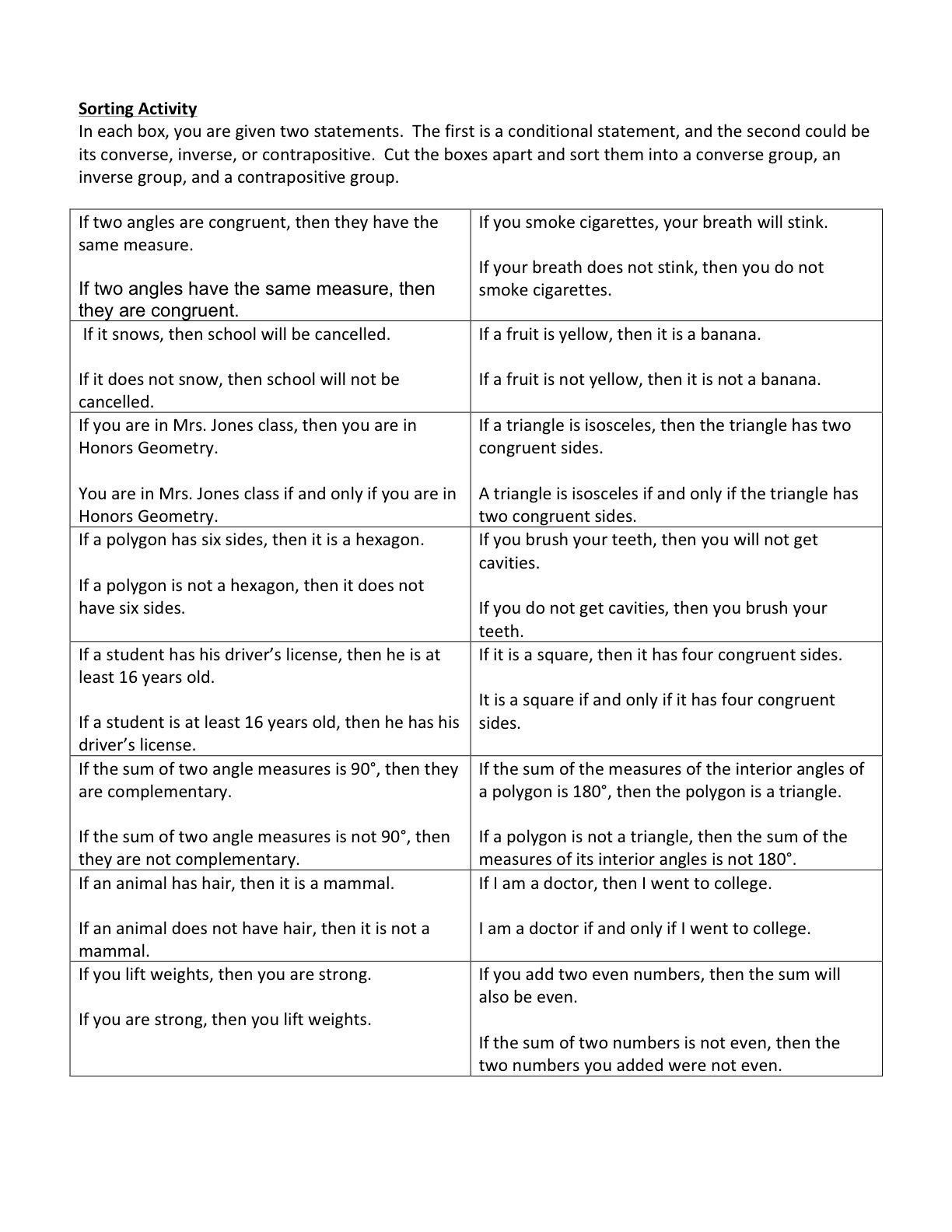
2. Practice with Conditional Statements Worksheets

Worksheets focusing on conditional statements provide structured practice:
- Identify the parts of the statement. Can you clearly separate the hypothesis from the conclusion?
- Translate sentences into if-then statements. This helps in seeing different ways to express geometric relationships.
- Use worksheets to explore converse, inverse, and contrapositive forms of statements, which are essential in understanding geometric proofs.
These exercises sharpen your ability to dissect and reconstruct logical arguments, a skill crucial for geometry.
3. Visualizing with Diagrams

Geometry is visual; hence, diagrams are not just aids but are integral to understanding. Use worksheets to:
- Sketch geometric figures that correspond to the conditions given in statements.
- Illustrate the implications of the statements by drawing consequences or what-if scenarios.
- Develop your spatial reasoning by trying to visualize three-dimensional scenarios from two-dimensional diagrams.
📏 Note: Practice drawing diagrams quickly and accurately to enhance your ability to visualize geometric problems.
4. Applying Real-World Scenarios

Geometry is not just about theorems and proofs; it’s also about recognizing patterns in the real world:
- Use real-life objects to explore conditional statements. For example, if a ladder leans against a wall at a certain angle, then what can you conclude about the ladder’s stability?
- Work through real-world scenarios on your worksheets, translating observations into if-then statements.
This application fosters a deeper understanding of how geometry operates in the physical world.
5. Peer Discussion and Collaborative Learning

Geometry benefits greatly from collaborative efforts:
- Engage in group study sessions where you can discuss conditional statements. Sharing and critiquing each other’s interpretations can lead to new insights.
- Work on proof problems together, discussing how to form conditional statements as part of the proof process.
- Create a collaborative worksheet where each member contributes statements or problems, then work through them as a team.
By integrating these five strategies into your study routine, you pave the way for mastery in geometry. Each strategy not only reinforces your understanding of conditional statements but also hones your analytical and problem-solving skills in geometric contexts. Remember, mastery in geometry is not just about memorizing formulas but about understanding the why behind the shapes and structures.
What are conditional statements in geometry?
+
Conditional statements in geometry are logical statements in the form of “if P, then Q,” where P (the hypothesis) leads to Q (the conclusion). They are fundamental in constructing proofs and understanding geometric relationships.
How can worksheets help in understanding geometry?

+
Worksheets provide structured practice, allowing you to work through different types of problems, visualize geometric concepts, and reinforce logical thinking, making abstract concepts more concrete and understandable.
Why is visualization important in geometry?

+
Visualization in geometry aids in understanding the spatial relationships and properties of shapes, making abstract ideas tangible. It helps in problem-solving by providing a mental or physical representation of geometric problems.
Can I apply geometry in everyday life?

+
Absolutely! Geometry is evident in architecture, design, art, engineering, and many other fields. Understanding geometric principles helps in appreciating and solving real-world problems involving spatial relationships and shapes.
How does peer discussion aid in mastering geometry?

+
Peer discussion promotes diverse perspectives, exposes you to different problem-solving methods, and allows for collaborative learning where students can teach each other, reinforcing their understanding and application of geometric concepts.