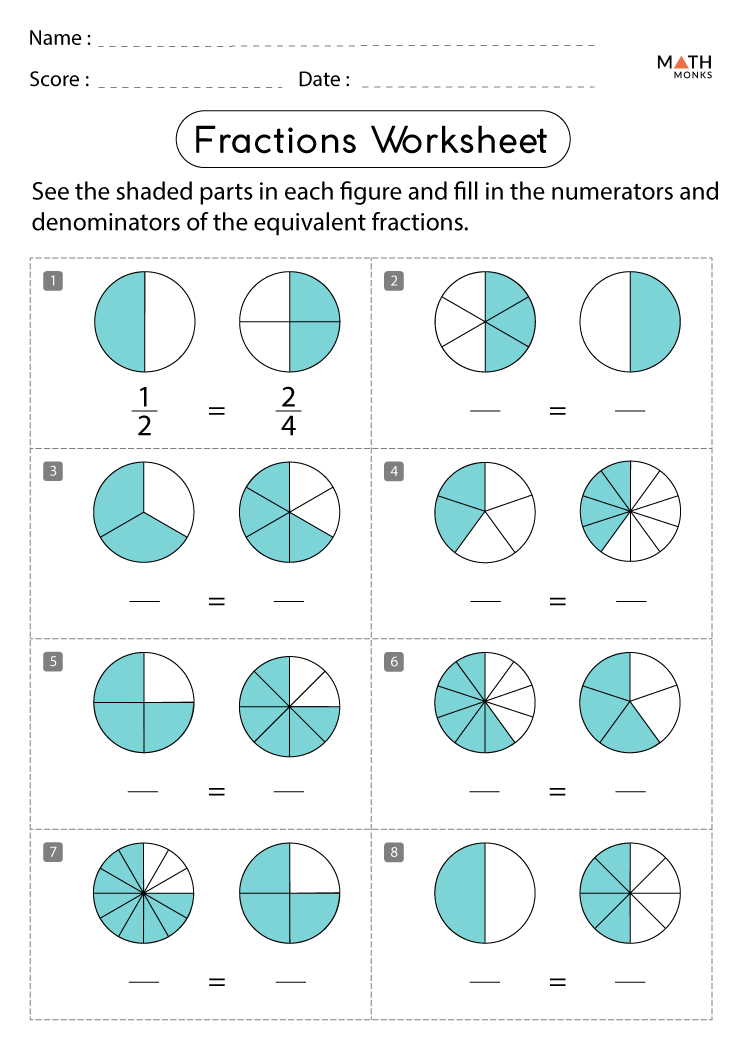
5 Ways to Condense Logarithms Effectively

Logarithm Simplification Techniques
Understanding the mechanics of logarithms can be a pivotal point in mastering higher mathematics. Logarithms are not only prevalent in exponential growth and decay problems but also essential in simplifying complex computations in areas such as physics, chemistry, and finance. Here's an in-depth look at five effective ways to condense logarithms:
1. Using Logarithmic Properties

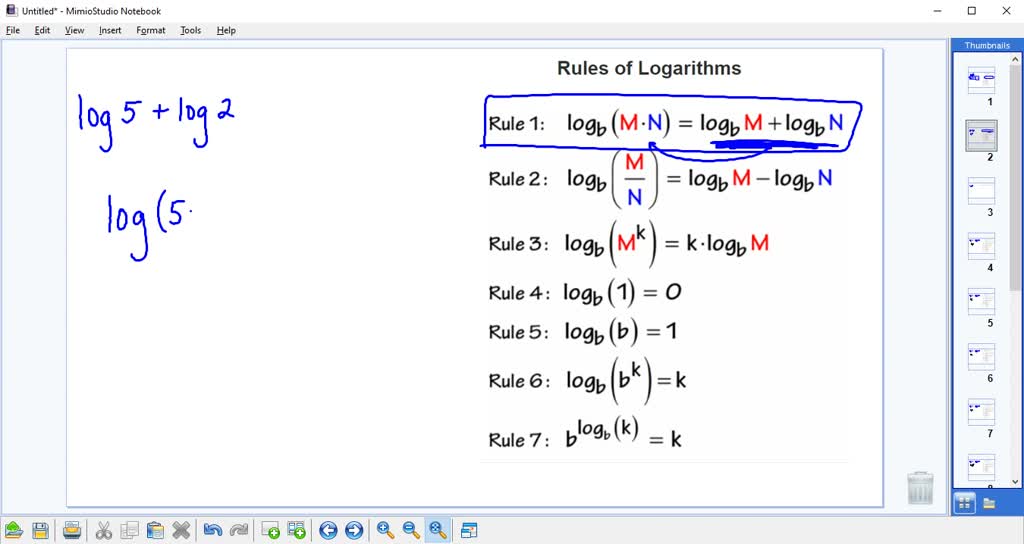
Logarithms obey several fundamental properties which can be used to combine or simplify multiple logarithms into a single expression. Here are the key properties:
- Product Rule:
log_b(M) + log_b(N) = log_b(MN) - Quotient Rule:
log_b(M) - log_b(N) = log_b(M/N) - Power Rule:
log_b(M^p) = p * log_b(M)
By understanding these rules, you can consolidate logarithms with the same base. For example:
log_2(5) + log_2(7) = log_2(5 * 7) = log_2(35)log_10(15) - log_10(5) = log_10(15/5) = log_10(3)
2. Change of Base Formula

If you have logarithms with different bases, or if the base is not in your preferred system, you can use the Change of Base Formula:
log_b(M) = log_k(M) / log_k(b)
This allows you to convert logarithms to a common base, often to base 10 (common log) or base e (natural log) for easier computation:
log_5(20) = log(20) / log(5) ≈ 2.287
💡 Note: You can use a calculator with logarithmic functions to simplify this process.
3. Simplifying Logarithmic Expressions

Often, logarithmic expressions can be simplified by factoring or using algebraic manipulation. Here are two approaches:
- Factoring: Factor out common terms to condense expressions.
- Algebraic Manipulation: Use laws of exponents or algebraic identities to simplify:
| Original Expression | Factored Form | Condensed Form |
|---|---|---|
| log(6) + log(x) | log(6) + log(x) = log(6x) | log(6x) |
| 2log(x) - log(x^2) | 2log(x) - log(x^2) = 2log(x) - log(x)^2 | log(x^2) - log(x^2) = log(x^0) = log(1) = 0 |

💡 Note: Always check for common factors or algebraic identities before attempting to condense logarithms.
4. Using Logarithmic Identities

Logarithmic identities can be used to condense complex expressions. Here are a couple of useful identities:
log_b(b^x) = xlog_b(1) = 0andlog_b(b) = 1log_b(1/a) = -log_b(a)
These identities help when simplifying expressions involving logarithms:
log_10(10^2) = 2log_2(1/8) = -3
5. Logarithmic Transformations

When dealing with functions or expressions involving exponential terms, logarithmic transformations can simplify the analysis:
- Transforming Equations: Use logarithms to transform an exponential equation into a linear one for easier analysis or graphing.
- Modeling Growth: Apply logarithms to understand exponential growth or decay in models like population growth or radioactive decay.
The final paragraph of your blog post: By mastering these five techniques for condensing logarithms, you'll unlock the ability to simplify complex expressions, making calculations more manageable and understanding mathematical concepts more straightforward. These methods not only aid in problem-solving but also enhance your analytical toolkit for various fields of study and practical applications.
Why are logarithms useful in real-world applications?

+
Logarithms are essential in fields like engineering, finance, and sciences for simplifying calculations, analyzing data with exponential trends, and solving complex equations involving large numbers.
What is the difference between the common logarithm and the natural logarithm?

+
The common logarithm (log base 10) is used in many engineering and scientific calculations, while the natural logarithm (log base e, or ln) is useful in mathematical modeling, physics, and finance where exponential growth or decay is involved.
How can I remember logarithmic rules and identities?

+
Practice is key! Regularly work through logarithmic problems, create flashcards, and use mnemonic devices or visual aids to help commit these rules to memory.
Can logarithms always be condensed?

+
Not always. Sometimes, you might need to expand or maintain the logarithmic form for certain types of analysis or when the logarithmic expression itself is more intuitive or informative than its condensed form.
What are the common mistakes when condensing logarithms?

+
Common mistakes include forgetting the sign of the logarithm, incorrectly applying rules when the bases are different, and not simplifying to the fullest extent possible.