5 Ways to Master Compound Volume Calculations

Understanding how to calculate the volume of composite shapes or compound volumes is crucial in various fields like engineering, architecture, and education. This skill not only enhances problem-solving capabilities but also boosts spatial awareness and logical thinking. Here are five effective strategies to master the art of compound volume calculations.
1. Understand Basic Volume Formulas


The first step in tackling complex volume problems is mastering the basic formulas for simple shapes such as:
- Rectangular Prism - Volume = Length × Width × Height
- Cube - Volume = Side3
- Cylinder - Volume = πr2 × Height
- Sphere - Volume = (4/3)πr3
- Cone - Volume = (1/3)πr2 × Height
- Pyramid - Volume = (1/3)Base Area × Height
🔍 Note: Ensure you're familiar with the units of measurement used in these formulas to avoid errors in calculations.
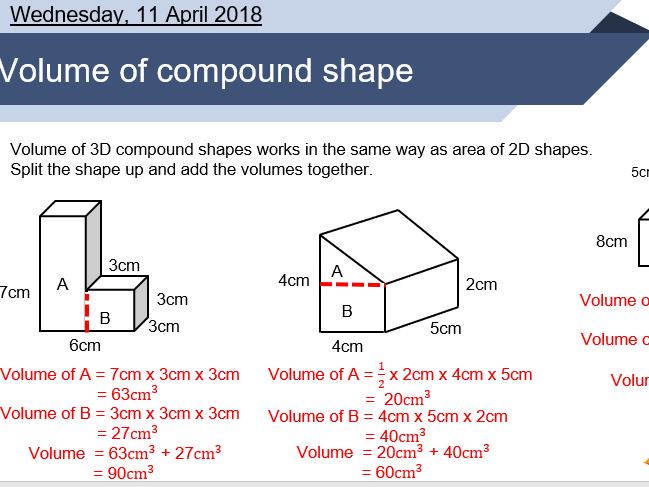
2. Break It Down: Decomposition Method

Compound volumes are often made up of several basic geometric shapes. Here's how you can apply the decomposition method:
- Identify the Shapes: Look at the compound object and identify individual shapes within it.
- Calculate Individually: Use the appropriate formula to calculate the volume of each shape separately.
- Sum or Subtract: If parts are added together, sum their volumes. If some parts are cut out, subtract these volumes from the total.
⚠️ Note: Ensure all units of measurements are consistent before adding or subtracting volumes.
3. Visualize with 3D Modeling


Using 3D modeling software or even sketching on paper can help visualize compound volumes:
- Use Software Tools: Software like AutoCAD, SketchUp, or Blender can provide a visual representation of the shapes.
- Sketching: If software isn't available, sketching the compound shape with different angles helps in understanding the volume composition.
👁 Note: Visualization can significantly reduce errors in calculations by confirming the shape's dimensions and composition.
4. Practice with Real-life Applications

Engaging with real-world objects can make learning compound volume calculations more practical:
- Architecture: Calculate the volume of buildings or sections within them.
- Manufacturing: Volume of machine parts or packaging.
- Cooking: Volumes in different shaped containers for food preparation.
- Sports: How much water a pool can hold or the volume of a ball.
🍽 Note: Applying theory to everyday objects enhances understanding and retention of volume calculation methods.
5. Use Online Calculators and Tutorials


Online tools can be invaluable for both beginners and experts:
- Interactive Calculators: Websites like Wolfram Alpha or specific volume calculators provide instant results and often show the steps.
- Video Tutorials: Platforms like YouTube offer step-by-step guides on how to approach complex volume problems.
- Learning Communities: Forums like Stack Exchange or educational platforms can help clarify doubts and offer peer-reviewed solutions.
🌐 Note: Be cautious with automated tools as they might not always account for unique or complex shapes accurately.
These five strategies provide a robust framework for mastering compound volume calculations. By understanding basic volume formulas, breaking down complex shapes, visualizing through modeling, applying practical knowledge, and utilizing online resources, you can become proficient in calculating the volumes of the most intricate shapes. This proficiency not only enhances your technical skills but also improves your ability to solve real-world problems where volume plays a crucial role.
Why is it important to know compound volume calculations?

+
Mastering compound volume calculations is essential for professionals in fields such as engineering, architecture, and product design where accurate volume measurement of complex shapes is necessary for design, manufacturing, and material estimation.
How can software tools assist in calculating compound volumes?

+
3D modeling software allows for the visualization of shapes in three dimensions, enabling users to accurately model and measure compound volumes. This visual aid can reduce errors in calculations and provide a better understanding of the spatial relationships between shapes.
Are there any shortcuts or common mistakes to avoid when calculating volumes?
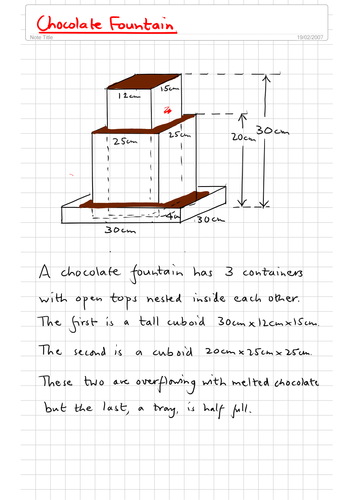
+
While there are no universal shortcuts, common mistakes include:
- Not converting all measurements to the same unit before calculating
- Using the wrong formula for specific shapes
- Forgetting to subtract volumes of cut-out parts in a compound shape
Can compound volume calculations help in my everyday life?

+
Yes, understanding volumes can help in various daily scenarios like:
- Determining the amount of water or substances needed for pools, ponds, or containers.
- Calculating the capacity of storage spaces or cargo in vehicles.
- Estimating the amount of paint or materials needed for home improvements.
What if the shape I’m working with isn’t perfectly geometric?

+
For irregular shapes, one can approximate volumes by:
- Using calculus for more complex shapes, like methods of slices or shells.
- Breaking down the shape into more manageable parts and calculating each part’s volume separately, then adding or subtracting as necessary.