5 Tips for Mastering Compound Inequalities in Algebra 1

Compound inequalities, a vital topic in Algebra 1, can often feel overwhelming at first. However, with the right approach, they become an exciting puzzle rather than a daunting task. This post delves into five essential tips for mastering compound inequalities, helping you to tackle these problems with confidence.
Understand the Basic Concept

Understanding compound inequalities is the first step towards mastering them. A compound inequality is essentially a combination of two or more simple inequalities joined by words like "and" or "or". Here's a brief breakdown:
- AND Inequalities: This type is true only when both inequalities are satisfied simultaneously. For example, 3 \leq x \leq 7 means x is between 3 and 7, inclusive.
- OR Inequalities: This type is true if either of the inequalities holds. For instance, x < 5 OR x > 8 includes all numbers less than 5 and all numbers greater than 8.

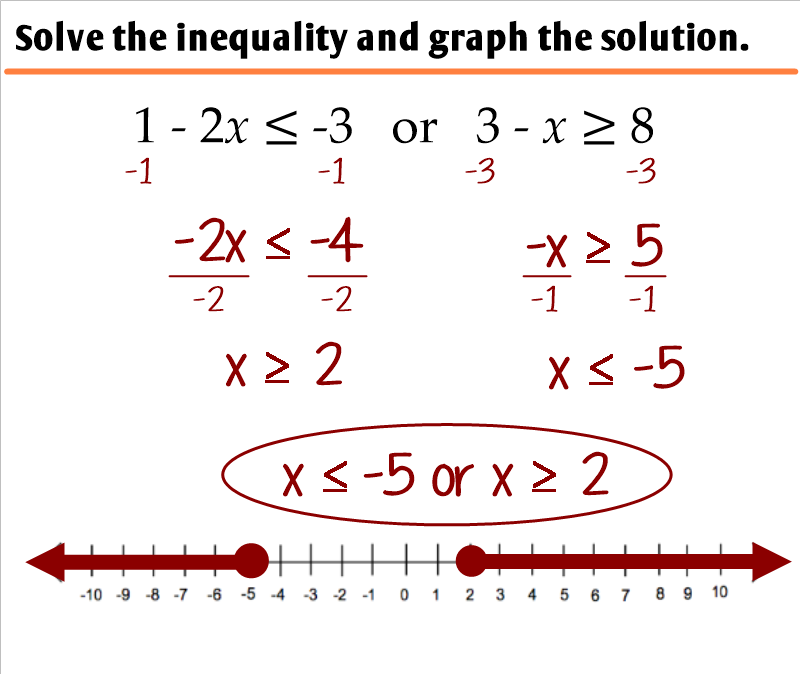
Master the Graphical Representation

Graphical representation can greatly aid in understanding compound inequalities. Here are the steps to graph them:
- Identify the Number Line: Start by drawing a number line.
- Plot the Simple Inequalities: For an "AND" inequality, find the overlapping region of the two inequalities. For "OR", show all points that satisfy at least one inequality.
- Use Open or Closed Circles: Solid circles for inclusion (inclusive), open circles for exclusion (non-inclusive).

📘 Note: Graphing compound inequalities visually illustrates the solution set, making it easier to understand the conditions under which the inequality holds true.
Practice Solving Linear Equations First

A strong foundation in solving linear equations is beneficial before tackling compound inequalities:
- Learn to solve equations involving addition, subtraction, multiplication, and division.
- Get comfortable with isolating variables to understand how inequalities work with variables.
Apply the Properties of Inequalities
Just like in equations, certain properties apply to inequalities:
| Property | Description |
|---|---|
| Addition/Subtraction | Add or subtract the same value from both sides without changing the inequality sign. |
| Multiplication/Division | Multiply or divide by the same positive value without changing the inequality sign. If the value is negative, reverse the inequality. |
| Transitivity | If a < b and b < c, then a < c. |

Let's illustrate with an example:
If x + 2 > 7, you can subtract 2 from both sides to get x > 5.
Work Through Real-World Applications

Compound inequalities are not just abstract math; they have practical uses:
- Budgeting: For example, if you need to buy an item costing between $10 and $30, you can express this as 10 \leq x \leq 30, where x is the amount you can spend.
- Health and Nutrition: Your daily caloric intake might need to be between 2,000 and 2,500 calories.
- Business: A manufacturer might require their product dimensions to be within certain limits for optimal performance.
💡 Note: Practice with real-world applications not only helps in understanding compound inequalities but also reinforces the practical significance of mathematics in everyday life.
By combining these five tips, you'll gain a strong command of compound inequalities. Remember that each tip builds upon the last, creating a comprehensive understanding of this algebraic topic. Through understanding the concepts, graphing, practicing linear equations, applying the correct properties, and relating them to real-world scenarios, you'll enhance your problem-solving skills, making compound inequalities a part of your everyday algebra toolkit.
What is the difference between “AND” and “OR” inequalities?

+
“AND” inequalities require both conditions to be true for the inequality to hold. “OR” inequalities need at least one condition to be true.
Why do we flip the inequality sign when multiplying or dividing by a negative number?

+
When you multiply or divide both sides of an inequality by a negative number, the relationship between the numbers changes, so you flip the inequality sign to maintain the correct relationship.
How can I practice compound inequalities?

+
Practice by solving linear equations first, then move on to inequalities. You can find numerous practice problems online, or even create your own scenarios involving budgeting or nutrition to make it more engaging.