5 Tips for Solving Compound Inequalities Easily

In today's mathematical landscape, compound inequalities play an essential role in both algebra and advanced calculus, serving as tools for problem-solving across various fields. They can appear complex at first glance, but with the right approach, solving them can be straightforward and rewarding. This blog post will guide you through five practical tips to simplify the process of tackling compound inequalities, ensuring you're well-equipped to handle them with confidence.
Understanding Compound Inequalities

What are compound inequalities? Compound inequalities are inequalities that consist of more than one inequality statement linked by either "and" or "or." For example, x \leq 3 and x > -5 joined to form -5 < x \leq 3.
📚 Note: Compound inequalities can be either "and" or "or" statements. An "and" statement requires both inequalities to be true for the variable to fall within the solution set. Conversely, an "or" statement requires at least one inequality to be true.
Tip 1: Identify the Type of Compound Inequality

- "And" Inequalities: If you have an inequality like -1 \leq x \leq 5 , it means x must simultaneously satisfy both conditions.
- "Or" Inequalities: Here, x needs to satisfy at least one of the given conditions, like x \leq -2 or x \geq 7 .
💡 Note: Knowing the type of compound inequality helps in deciding how to approach the problem. "And" inequalities require a narrower solution set while "or" inequalities expand the range of possible solutions.
Tip 2: Solve Each Inequality Separately

Breaking down the compound inequality into its individual components allows for clearer analysis. Here’s how:
- Example: For the inequality -4 \leq 3x - 1 \leq 11 , first solve 3x - 1 \geq -4 and then 3x - 1 \leq 11.
- By solving 3x - 1 \geq -4, you get x \geq -1.
- Solving 3x - 1 \leq 11 gives x \leq 4.
- The combined solution is -1 \leq x \leq 4 .
🔧 Note: Each inequality provides boundaries for your variable. Treating them individually ensures you capture all potential solutions accurately.
Tip 3: Combine Your Solutions

After solving each inequality, you must:
- "And" Inequalities: Find the overlap between the solutions. This is the interval where the variable must fall to satisfy both inequalities.
- "Or" Inequalities: Combine all intervals where at least one inequality is true. Here, you might find that solutions are separate intervals.
| Inequality | Solution Sets | Combined Solution |
|---|---|---|
| x \leq 3 | (-∞, 3] | (-∞, 3] ∪ (4, ∞) |
| x > 4 | (4, ∞) |

📝 Note: Visualization can be key. Sketching a number line might help in understanding the solution set better, especially for "or" inequalities where the solution could be disjointed.
Tip 4: Check Boundary Points

Boundary points can be critical in determining the correct solution set, especially in "and" inequalities. Here’s what you need to do:
- Example: For 1 \leq x < 5, you check if x = 1 and x = 5 are included in the solution.
- Substitute x = 1 into the original inequalities, 1 \leq 1 is true, but 1 < 5 is false, so x = 1 does not work.
- Substitute x = 5 into the original inequalities, 5 \leq 5 is true, but 5 < 5 is false, so x = 5 does not work either.
- Therefore, 1 < x < 5.
🎯 Note: Always verify if boundary points satisfy both inequalities in "and" statements or one inequality in "or" statements to avoid common mistakes.
Tip 5: Apply Real-World Context

Compound inequalities aren't just theoretical; they have practical applications:
- Example: Imagine you have 50 < M < 70 for the percentage of moisture content in soil for a certain plant to thrive. Here, M must fall between these values.
- By applying our tips, you can quickly determine the acceptable range and make informed decisions in real-life scenarios.
In summary, solving compound inequalities becomes much more manageable with these tips. Start by understanding the type of inequality, solve each part individually, combine your solutions logically, verify boundary points, and always consider the context. These strategies not only make the mathematical process smoother but also ensure that you understand the practical implications of your solutions. Remember that practice will solidify these tips, turning complex inequalities into straightforward problems you can tackle with ease.
What is the difference between an “and” and an “or” compound inequality?
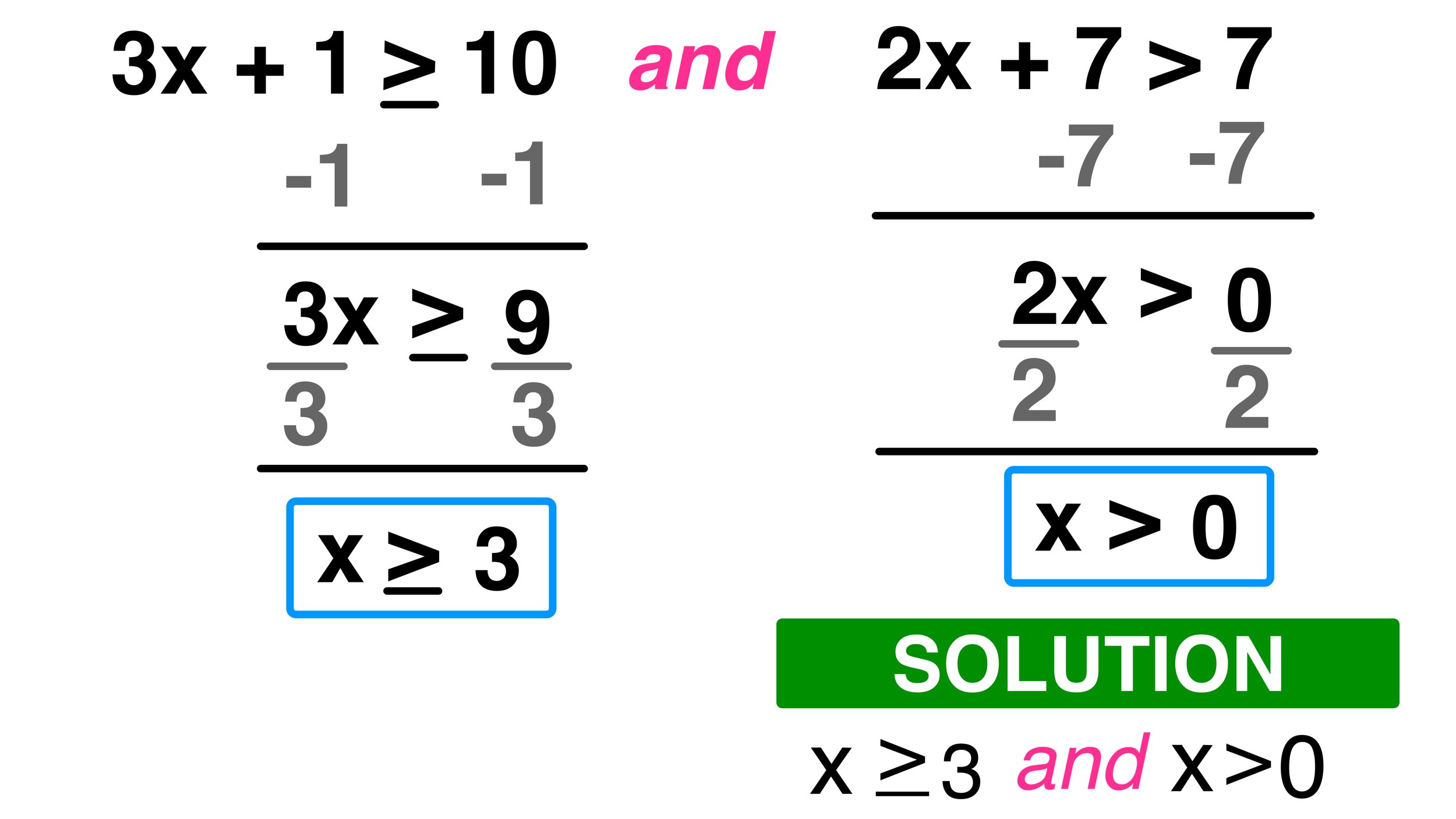
+
An “and” compound inequality requires both statements to be true simultaneously for the solution to hold true. An “or” compound inequality requires at least one of the statements to be true.
How do I solve a compound inequality with absolute values?

+
When dealing with absolute values in compound inequalities, you need to consider both the positive and negative aspects of the inequality. For example, if you have (|x-3| \leq 5), this means (x) must fall within the range where (x-3) is between -5 and 5, hence (-2 \leq x \leq 8).
Why are boundary points important in solving compound inequalities?
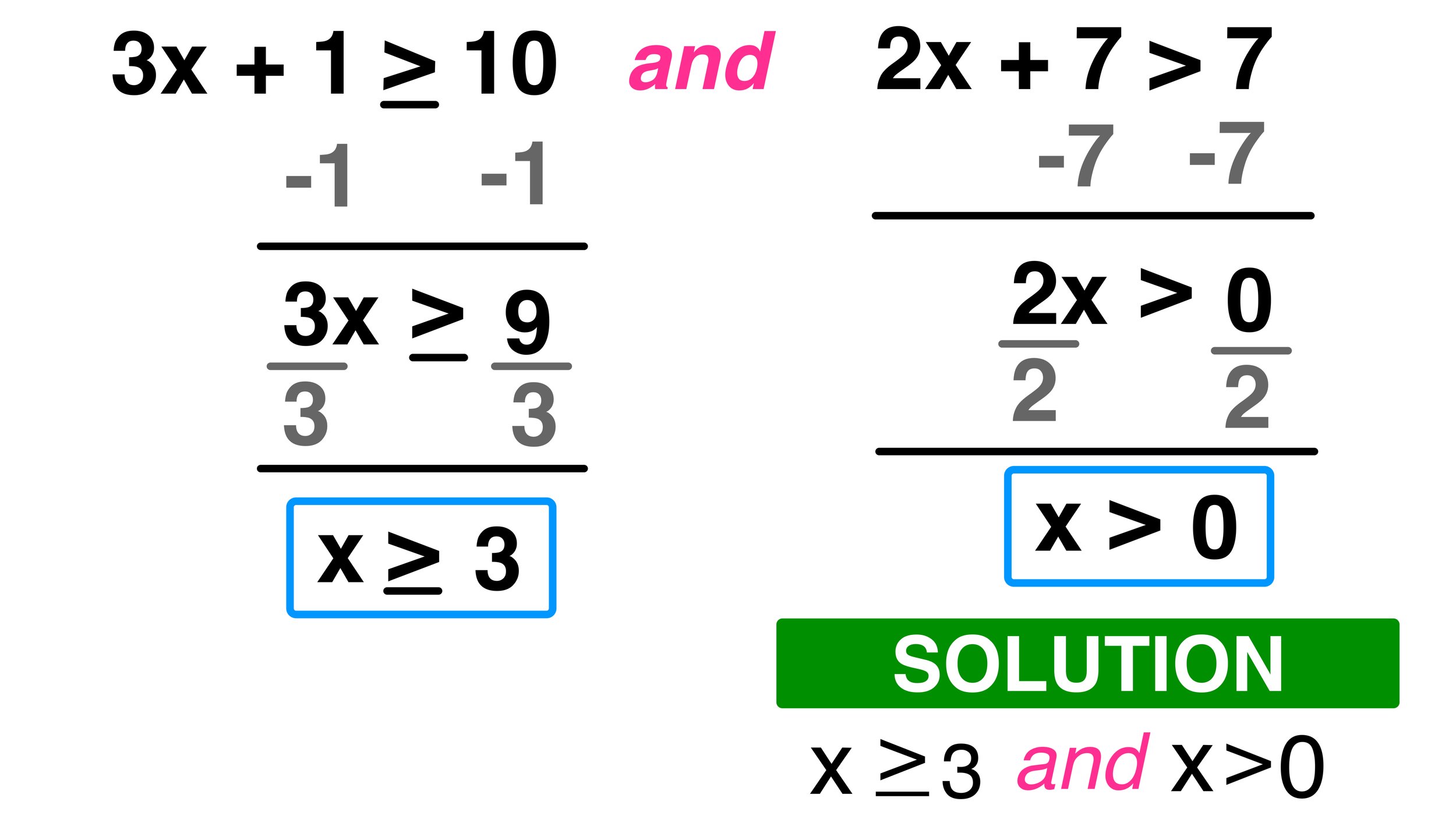
+
Boundary points determine the inclusion or exclusion of specific values in the solution set. Checking these points ensures that you correctly represent the inequality’s constraints, particularly when dealing with strict and non-strict inequalities.