Mastering Compound Area: Free Worksheet for Quick Learning

Understanding Compound Area
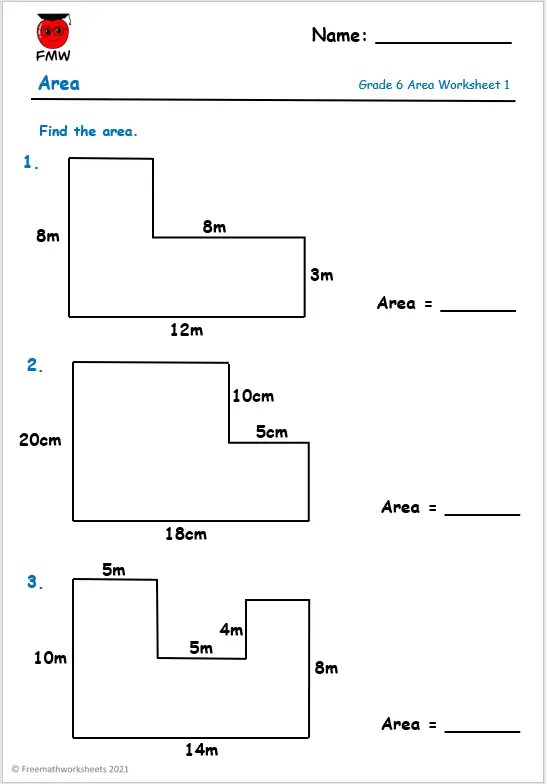
Compound area, often also referred to as composite area, involves calculating the area of shapes that are made up of two or more simple geometric figures, such as rectangles, triangles, circles, or any combination thereof. This concept is crucial in both practical and theoretical mathematics, touching on fields from architecture to graphic design. In this blog post, we delve into the intricacies of compound area calculation, providing you with a comprehensive understanding and a free worksheet for quick learning.
What is Compound Area?

Compound or composite shapes are not the straightforward geometric figures you studied in elementary geometry. These are shapes formed by combining two or more basic geometric shapes where their perimeters partially or wholly coincide. Here’s a simple breakdown:
- Individual Shapes: Understand the basic shapes involved.
- Overlapping Regions: Identify and handle parts where shapes overlap.
- Add or Subtract: Depending on whether shapes add area or exclude it from the total.
Consider a scenario where you need to calculate the area of a house’s floor plan or design a garden with curved paths and flower beds. Knowledge of compound area calculation is indispensable.
Steps to Calculate Compound Area

Here’s a detailed guide to calculating the area of a compound shape:
1. Break Down the Compound Shape
The first step involves recognizing the individual shapes that make up the compound shape. For example, if a shape consists of a rectangle with a semi-circle on top:
- Identify: A rectangle and a semi-circle.
- Dimensions: Note the dimensions of each shape.
2. Calculate Each Shape's Area
Calculate the area of each individual shape separately:
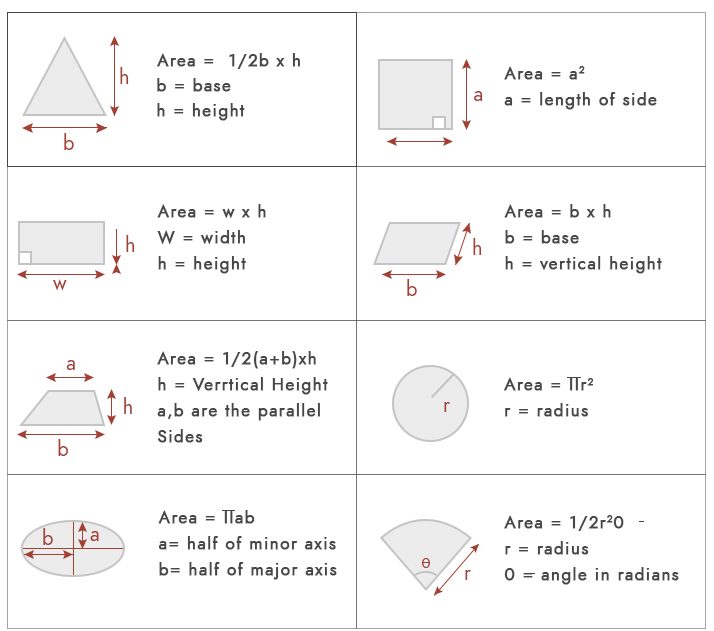
- Rectangle: Area = length × width
- Semi-circle: Area = (π × radius2)/2
3. Combine or Subtract Areas
This step depends on how the shapes are arranged:
- If shapes are added together:
- Sum: Total Area = Area of Shape A + Area of Shape B + ...
- If shapes overlap:
- Subtract: Total Area = Area of Shape A + Area of Shape B - Area of Overlap
4. Cross-check Your Calculations
It’s always a good practice to double-check your calculations:
- Use alternate methods like squaring dimensions for verification.
- Consider units (e.g., square meters, square feet) for consistency.
Practical Applications
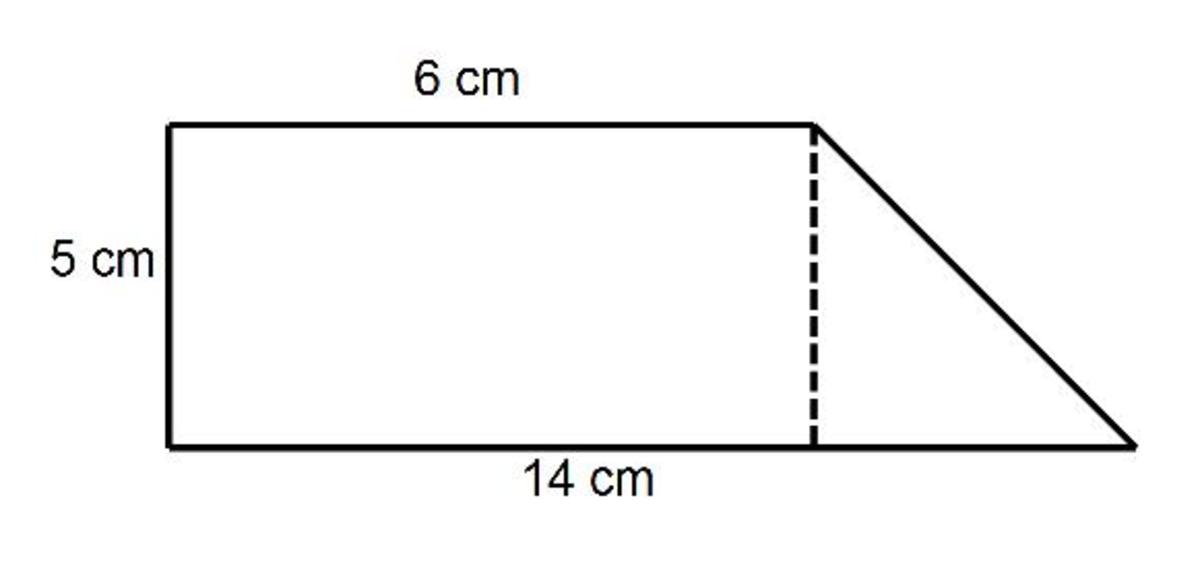
The ability to calculate compound area has numerous practical applications:
- Architecture: Designing floor plans, landscaping.
- Art and Design: Creating abstract or geometric artwork.
- Civil Engineering: Building structures, calculating road surfaces.
Free Compound Area Worksheet
To help you grasp the concept better, we’ve crafted a free worksheet which includes a variety of compound shapes for you to practice:
📝 Note: This worksheet is meant for educational purposes, and by practicing with it, you can significantly improve your understanding of compound area calculation.
| Shape | Individual Areas | Total Area |
|---|---|---|
| Shape A: Rectangle + Semi-circle | Rectangle: 6 × 8 m, Semi-circle: (π × 22) / 2 | (6 × 8) + ((π × 4) / 2) = 48 + 6.28 = 54.28 m2 |
| Shape B: Triangle - Small Rectangle | Triangle: ½ (8 × 6) = 24, Rectangle: 2 × 2 = 4 | 24 - 4 = 20 m2 |
| Shape C: Quadrilateral (Combination of Shapes) | Square: 4 × 4 = 16, Circle: π × 22 = 12.56 | 16 + 12.56 = 28.56 m2 |

The wrap-up of this journey through compound areas not only broadens your understanding but also equips you with the skills necessary for practical applications. Whether you're planning a new construction, designing an innovative project, or simply solving complex mathematical problems, mastering compound area calculation ensures accuracy and efficiency in your work.
Why is compound area important in real-world applications?
+
Understanding compound area allows for precise calculations in various industries like construction, architecture, and design, ensuring space utilization is optimized and materials are estimated accurately.
Can I use a calculator for compound area calculations?

+
Yes, calculators and geometric software can simplify the process, especially for complex shapes with multiple components or where high precision is required.
What common mistakes should I avoid when calculating compound areas?
+
Watch out for errors like double-counting overlapped areas, misjudging shape dimensions, or incorrectly adding or subtracting areas based on the shape layout.
Related Terms:
- Compound area worksheet pdf
- Compound area worksheet with answers