5 Composite Functions Tips with Answer Sheet

Composite functions, often referred to as functions of functions, are an essential concept in algebra and calculus. They allow you to combine multiple functions to create a more complex function. Understanding how to work with composite functions can be invaluable for students tackling advanced mathematics, engineers designing complex systems, or analysts modeling financial scenarios. Here are five tips to master composite functions along with an answer sheet to common problems that can help you develop a deeper understanding of this concept.
1. Understand the Notation

Composite functions are usually represented in mathematics with a notation like (f(g(x))), which means apply function (g) to (x) first and then apply (f) to the result. Here are some tips to ensure you get the notation right:
- Inner and Outer Functions: Identify which function is the inner one (g) and which is the outer one (f). This is crucial for correctly applying the functions.
- From Right to Left: When reading a composite function notation like (f(g(h(x)))), start from the right with the innermost function and move outward. That is, (h(x)) is first applied, then (g), then (f).
- Use Brackets: Brackets are used to denote the composite function clearly. If you’re unsure, add extra brackets for clarity, like (f(g(x))) instead of (fg(x)).
👉 Note: Remember that the order matters in composite functions. (f(g(x))) is not necessarily equal to (g(f(x))).
2. Learn to Decompose Functions

Sometimes you need to break down a complex function into simpler parts. This process is called decomposing. Here’s how to go about it:
- Identify Components: Look for parts of the function that can stand alone as individual functions.
- Work Backwards: If you know what the composite function should be, you can work backwards to find the component functions.
- Check Your Work: After decomposing, compose the functions again to see if you get the original function back.

👉 Note: Decomposing functions isn’t always unique; there can be multiple valid ways to break down a function.
3. Practice Evaluating Composite Functions
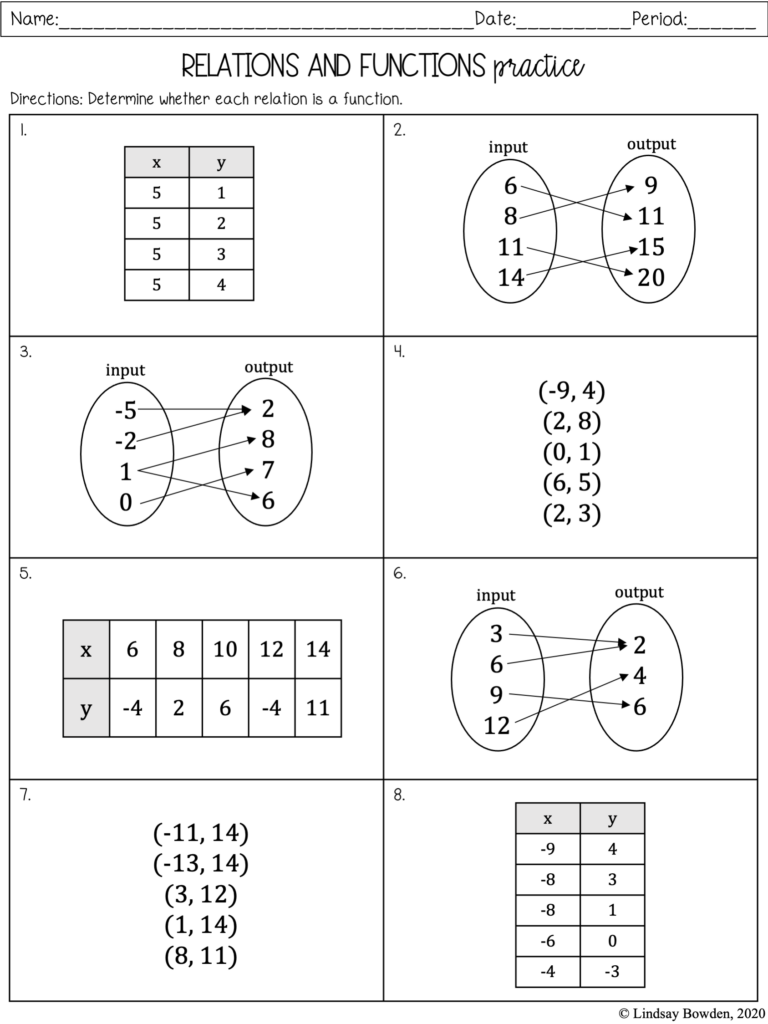
Evaluating composite functions involves plugging in one function into another. Here’s how you can practice:
- Step-by-Step Evaluation: Write out each step of the evaluation process to see how the functions interact.
- Use Substitution: Substitute the inner function into the outer function carefully to avoid errors.
- Check for Domain Restrictions: Remember that composing functions can change the domain, so always check if the final function’s domain is valid.
👉 Note: Keep track of your variables, especially when dealing with multiple functions. Using different letters for variables can reduce confusion.
4. Work Through Composite Function Inverses

The inverse of a composite function often comes up in calculus and advanced algebra. Here are some strategies:
- Find Individual Inverses: Start by finding the inverse of each function individually.
- Compose Inverses: The inverse of a composite function (f(g(x))) is (g^{-1}(f^{-1}(x))), but this requires careful order.
- Verify Your Inverse: After finding the inverse, check it by composing it with the original composite function to ensure you get the identity function (x).
5. Utilize a Composite Function Answer Sheet

Here’s a table with some common composite function problems along with their answers to help solidify your understanding:
| Problem | Answer |
|---|---|
| If (f(x) = 3x - 2) and (g(x) = x^2 + 1), find (f(g(x))). | (f(g(x)) = 3(x^2 + 1) - 2 = 3x^2 + 3 - 2 = 3x^2 + 1) |
| Given (h(x) = x - 4) and (k(x) = \sqrt{x}), find (k(h(x))). | (k(h(x)) = \sqrt{x - 4}) |
| If (f(x) = e^x) and (g(x) = \ln(x)), find (f(g(x))). | (f(g(x)) = e^{\ln(x)} = x) |
| Find the inverse of (f(g(x))) if (f(x) = 2x + 3) and (g(x) = \frac{1}{x}). | The inverse of (f(g(x))) is (g^{-1}(f^{-1}(x)) = \frac{1}{\frac{x - 3}{2}} = \frac{2}{x - 3}) |

By following these tips and practicing with the answer sheet, you'll enhance your comprehension of composite functions, ensuring you can tackle problems with confidence and accuracy. Whether you're preparing for an exam, working on a project, or simply exploring the beauty of mathematics, mastering composite functions is a valuable skill that opens up numerous possibilities in problem-solving and modeling.
What is the difference between function composition and function multiplication?

+
Function composition involves applying one function to the result of another, whereas function multiplication is simply the product of the two functions evaluated at a point.
How can I find the domain of a composite function?

+
The domain of a composite function (f(g(x))) is the set of all (x) for which both (g(x)) exists and (f(g(x))) is defined. Start by finding the domain of the inner function (g(x)) and then the domain of (f) applied to (g(x)).
Why do we need to decompose functions?
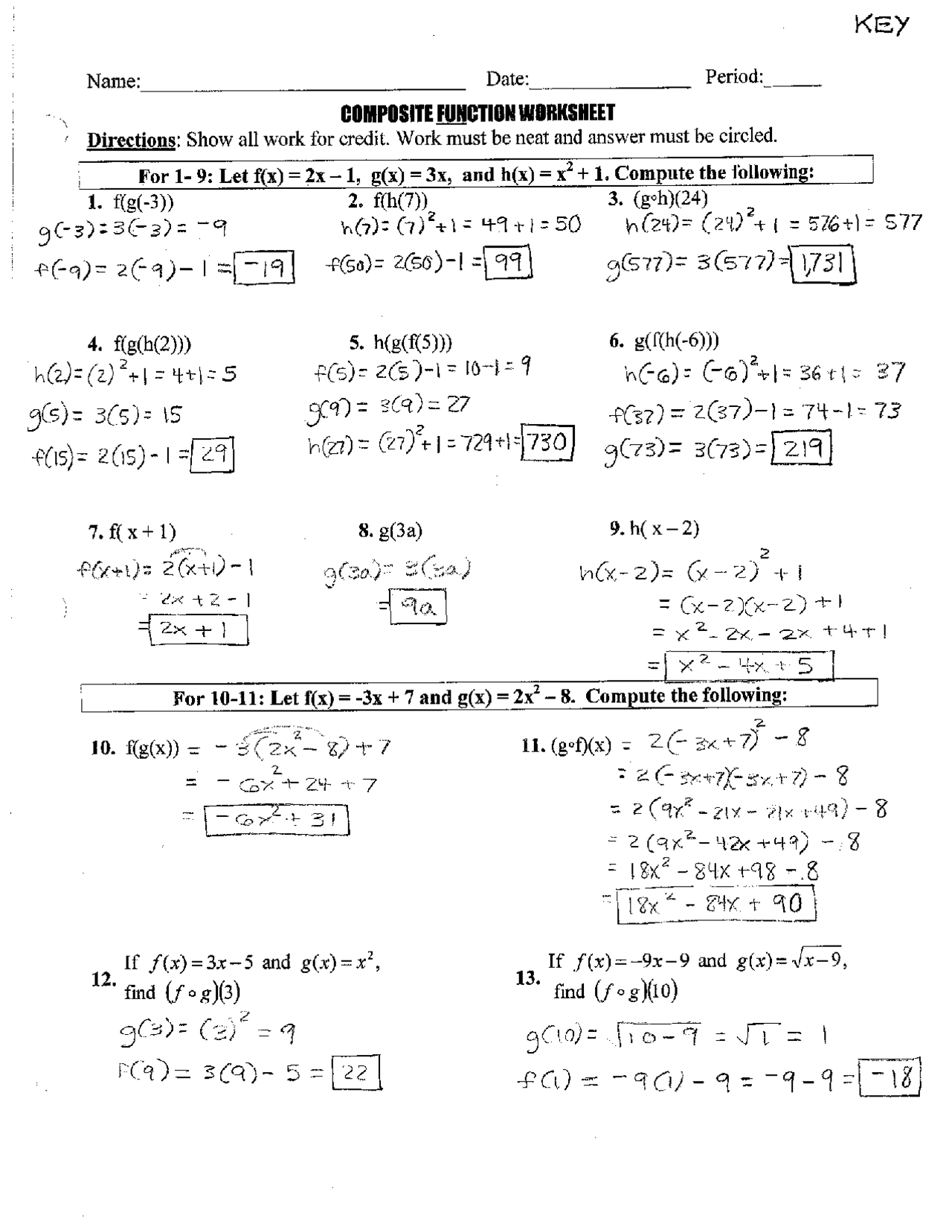
+
Decomposing functions helps in understanding complex functions, simplifies problem-solving, and can aid in finding derivatives or solving equations involving these functions.